EBK PHYSICS FOR SCIENTISTS & ENGINEERS
5th Edition
ISBN: 9780134296074
Author: GIANCOLI
Publisher: VST
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 11, Problem 85GP
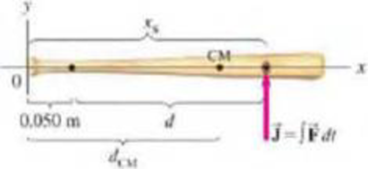
A baseball bat has a “sweet spot” where a ball can be hit with almost effortless transmission of energy. A careful analysis of baseball dynamics shows that this special spot is located at the point where an applied force would result in pure rotation of the bat about the handle grip. Determine the location of the sweet spot of the bat shown in Fig. 11–51. Tile linear mass density of the bat is given roughly by (0.61 + 3.3x2) kg/m, where x is in meters measured from the end of the handle. The entire bat is 0.84 m long. The desired rotation point should be 5.0 cm from the end where the bat is held. [Hint: Where is the CM of the bat?]
FIGURE 11–51 Problem 82.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The kinetic energy of a pendulum is greatest
Question 20Select one:
a.
at the top of its swing.
b.
when its potential energy is greatest.
c.
at the bottom of its swing.
d.
when its total energy is greatest.
Part a-D pl
The figure (Figure 1) shows representations of six
thermodynamic states of the same ideal gas sample.
Figure
1 of 1
Part A
■Review | Constants
Rank the states on the basis of the pressure of the gas sample at each state.
Rank pressure from highest to lowest. To rank items as equivalent, overlap them.
▸ View Available Hint(s)
highest
0
☐ ☐ ☐ ☐ ☐ ☐
Reset
Help
B
F
A
D
E
The correct ranking cannot be determined.
Submit
Previous Answers
× Incorrect; Try Again; 4 attempts remaining
Provide Feedback
lowest
Next >
Chapter 11 Solutions
EBK PHYSICS FOR SCIENTISTS & ENGINEERS
Ch. 11.1 - Prob. 1AECh. 11.1 - Suppose you are standing on the edge of a large...Ch. 11.1 - CONCEPTUAL EXAMPLE 115 Spinning bicycle wheel....Ch. 11.1 - For the vectors A and B in the plane of the page...Ch. 11.2 - Prob. 1EECh. 11.2 - Prob. 1FECh. 11 - Can the diver of Fig. 112 do a somersault without...Ch. 11 - When a motorcyclist leaves the ground on a jump...Ch. 11 - Suppose you are sitting on a rotating stool...Ch. 11 - Prob. 4Q
Ch. 11 - A shortstop may leap into the air to catch a ball...Ch. 11 - If all the components of the vectors V1 and V2...Ch. 11 - A force F=Fj is applied to an object at a position...Ch. 11 - A particle moves with constant speed along a...Ch. 11 - If the net force on a system is zero, is the net...Ch. 11 - Explain how a child pumps on a swing to make it go...Ch. 11 - Describe the torque needed if the person in Fig....Ch. 11 - An astronaut floats freely in a weightless...Ch. 11 - On the basis of the law of conservation of angular...Ch. 11 - A wheel is rotating freely about a vertical axis...Ch. 11 - Consider the following vector quantities:...Ch. 11 - How does a car make a right turn? Where does the...Ch. 11 - In a rotating frame of reference. Newtons first...Ch. 11 - Why is it that at most locations on the Earth, a...Ch. 11 - In the battle of the Falkland Islands in 1914, the...Ch. 11 - Prob. 1MCQCh. 11 - Prob. 4MCQCh. 11 - Prob. 5MCQCh. 11 - Prob. 6MCQCh. 11 - Prob. 7MCQCh. 11 - Prob. 8MCQCh. 11 - Prob. 9MCQCh. 11 - Prob. 10MCQCh. 11 - Prob. 11MCQCh. 11 - Prob. 1PCh. 11 - Prob. 2PCh. 11 - (II) A nonrotating cylindrical disk of moment of...Ch. 11 - (II) A diver (such as the one shown in Fig. 112)...Ch. 11 - Prob. 5PCh. 11 - Prob. 6PCh. 11 - Prob. 7PCh. 11 - Prob. 8PCh. 11 - Prob. 9PCh. 11 - (II) A person of mass 75 kg stands at the center...Ch. 11 - (II) A person stands on a platform, initially at...Ch. 11 - Prob. 12PCh. 11 - Prob. 13PCh. 11 - (II) A woman of mass m stands at the edge of a...Ch. 11 - Prob. 15PCh. 11 - Prob. 16PCh. 11 - (II) A uniform horizontal rod of mass M and length...Ch. 11 - (II) Suppose our Sun eventually collapses into a...Ch. 11 - (III) Hurricanes can involve winds in excess of...Ch. 11 - Prob. 21PCh. 11 - (I) If vector A points along the negative x axis...Ch. 11 - (I) Show that (a) i i = j j = k k = 0. (b) i j...Ch. 11 - (I) The directions of vectors A and B are given...Ch. 11 - (II) What is the angle between two vectorsA and...Ch. 11 - Prob. 26PCh. 11 - (II) Consider a particle of a rigid object...Ch. 11 - Prob. 29PCh. 11 - (II) An engineer estimates that under the most...Ch. 11 - Prob. 31PCh. 11 - Prob. 32PCh. 11 - Prob. 33PCh. 11 - (I) What are the x, y, and z components of the...Ch. 11 - (I) Show that the kinetic energy K of a particle...Ch. 11 - (I) Calculate the angular momentum of a particle...Ch. 11 - (II) Two identical particles have equal but...Ch. 11 - Prob. 38PCh. 11 - Prob. 39PCh. 11 - Prob. 40PCh. 11 - (II) Four identical particles of mass m are...Ch. 11 - (II) Two lightweight rods 24 cm in length are...Ch. 11 - (II) Figure 1135 shows two masses connected by a...Ch. 11 - (III) Show that the total angular momentum L=ripi...Ch. 11 - Prob. 45PCh. 11 - Prob. 46PCh. 11 - (II) A thin rod of mass M and length is suspended...Ch. 11 - Prob. 48PCh. 11 - Prob. 49PCh. 11 - Prob. 50PCh. 11 - Prob. 51PCh. 11 - (III) A thin rod of mass M and length rests on a...Ch. 11 - (III) On a level billiards table a cue ball,...Ch. 11 - Prob. 54PCh. 11 - (II) A toy gyroscope consists of a 170-g disk with...Ch. 11 - Prob. 56PCh. 11 - Prob. 57PCh. 11 - Prob. 58PCh. 11 - Prob. 60PCh. 11 - Prob. 61PCh. 11 - (II) Suppose the man at B in Fig. 1126 throws the...Ch. 11 - (II) For what directions of velocity would the...Ch. 11 - (III) We can alter Eqs. 1114 and 1115 for use on...Ch. 11 - (III) An ant crawls with constant speed outward...Ch. 11 - A thin string is wrapped around a cylindrical hoop...Ch. 11 - Prob. 67GPCh. 11 - Prob. 68GPCh. 11 - Why might tall narrow SUVs and buses be prone to...Ch. 11 - A projectile with mass m is launched from the...Ch. 11 - Prob. 71GPCh. 11 - Prob. 72GPCh. 11 - Prob. 73GPCh. 11 - Prob. 74GPCh. 11 - Prob. 75GPCh. 11 - Prob. 76GPCh. 11 - Prob. 77GPCh. 11 - Prob. 78GPCh. 11 - A particle of mass m uniformly accelerates as...Ch. 11 - Prob. 80GPCh. 11 - Most of our Solar Systems mass is contained in the...Ch. 11 - Competitive ice skaters commonly perform single,...Ch. 11 - Prob. 84GPCh. 11 - A baseball bat has a sweet spot where a ball can...Ch. 11 - Prob. 86GP
Additional Science Textbook Solutions
Find more solutions based on key concepts
What type of culture medium would increase the size of a bacterial capsule?
Laboratory Experiments in Microbiology (12th Edition) (What's New in Microbiology)
Two culture media were inoculated with four different bacteria. After incubation, the following results were ob...
Microbiology: An Introduction
Which type of cartilage is most plentiful in the adult body?
Anatomy & Physiology (6th Edition)
18. SCIENTIFIC THINKING By measuring the fossil remains of Homo floresiensis, scientists have estimated its wei...
Campbell Biology: Concepts & Connections (9th Edition)
33. Which statement about electrons is true?
a. Electrons attract one another.
b. Electrons are repelled by pro...
Introductory Chemistry (6th Edition)
10.71 Identify each of the following as an acid or a base: (10.1)
H2SO4
RbOH
Ca(OH)2
HI
...
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Part A m 2πkT ) 3/2 Calculate the integral (v) = f vƒ (v)dv. The function f(v) describing the actual distribution of molecular speeds is called the Maxwell-Boltzmann distribution, = ƒ(v) = 4π (· v²e-mv²/2kT . (Hint: Make the change of variable v² =x and use the tabulated integral foxne integer and a is a positive constant.) Express your answer in terms of the variables T, m, and appropriate constants. -ax dx n! - an+1 where n is a positive (v) = ΕΠΙ ΑΣΦ Submit Previous Answers Request Answer ? × Incorrect; Try Again; 4 attempts remaining Al Study Tools Looking for some guidance? Let's work through a few related practice questions before you go back to the real thing. This won't impact your score, so stop at anytime and ask for clarification whenever you need it. Ready to give it a try? Startarrow_forwardStarter the rule of significantarrow_forwardPlease solve this problem and give step by step explanations on each step while breaking it down please. Thank you!!arrow_forward
- Car A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B, will be 2 μF A 1 µF B 3 µFarrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed. NOT AI PLSarrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
Rotational Kinetic Energy; Author: AK LECTURES;https://www.youtube.com/watch?v=s5P3DGdyimI;License: Standard YouTube License, CC-BY