RESEARCH METHODS F/ BEHAV.(LL)-W/MINTAP
6th Edition
ISBN: 9781337755016
Author: GRAVETTER
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 11, Problem 7E
In Figure 11.5, we show three combinations of main effects and interactions for a 2 × 2 factorial design. Using the same 2 × 2 structure, with factor A defining the rows and factor B defining the columns, create a set of means that produce each of the following patterns:
a. A main effect for factors A and B, but no interaction.
b. A main effect for factor A and an interaction, but no main effect for factor B.
c. A main effect for both factors and an interaction.
FIGURE 11.5
Three Possible Combinations of Main Effects and Interactions in a Two-Factor Experiment.
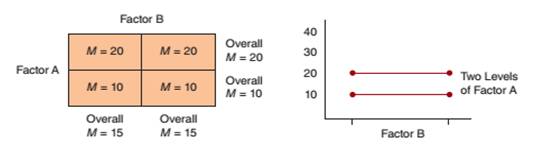
(a) Data showing a main effect for factor A but no main effect for factor B and no interaction.
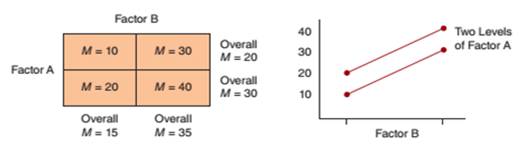
(b) Data showing main effects for both factor A and factor B but no interaction.
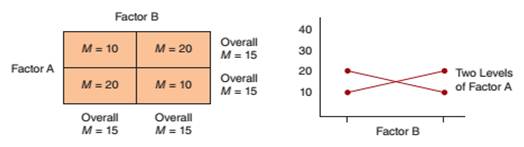
(c) Data showing no main effect for either factor, but an interaction.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Mr. Adams wants to rent a beachfront condominium. Unit 1 costs $1,200 for the week plus a cleaning fee of $50 per day. Unit 2 costs $1,450 for the week with no cleaning
fee.
What is an appropriate model to use to determine at which number of days both units cost the same amount for the week?
a table with two columns, one showing the cost of Unit 1 starting at $1,200 and increasing $50 every row, and the other showing the cost of Unit 2 starting at
$1,450 and increasing $50 each row
a graph with the number of days for the week on the x-axis and the cost on the y-axis, showing the cost of Unit 1 starting at $50 and increasing $1,200 each
day, and the cost of Unit 2 starting at $0 and increasing $1,450 each day
a graph w
the number of days for the
eek on the x-axis and the cost on
he y-axis, showing
cost
1 starting at $1,200 and increasing $50 each
day, and the cost of Unit 2 at $1,450 each day without increasing
a table with two columns, one showing the cost of Unit 1 starting at $50 and…
A plant biologist conducted an experiment to compare the yields of 4 varieties of
peanuts (A, B, C, D). A plot of land was divided into 16 subplots (4 rows and 4
columns). The plant biologist uses the design shown in Table Q2.
Table Q2
B = 29.0
C = 26.7
A = 23.1
B = 29.3
D = 25.1
D= 29.8
C = 29.0
A = 27.3
A =19.7
B = 21.7
D= 24.9
C = 29.0
A = 28.7
D= 20.1
C =17.4
B= 35.1
What is the most appropriate design for this problem? State the statistical model
with the necessary assumptions and identify the terms.
(a)
(b)
Is the design symmetric? Justify your answer.
(c)
Analyze these data with the appropriate conclusions. (Use a = 0.05).
State the concept of Row switching?
Chapter 11 Solutions
RESEARCH METHODS F/ BEHAV.(LL)-W/MINTAP
Ch. 11.1 - Define a factorial research design, including the...Ch. 11.2 - Define a main effect for one factor and an...Ch. 11.2 - Explain how the existence of an interaction can...Ch. 11.2 - Describe and explain the independent relationship...Ch. 11.3 - Explain how a factorial study can combine...Ch. 11.3 - Identify the statistical analyses that are...Ch. 11.4 - Describe three specific applications of the...Ch. 11 - In addition to the key words, you should also be...Ch. 11 - In a classic study, Shrauger (1972) examined the...Ch. 11 - Suppose a researcher conducts a two-factor study...
Ch. 11 - The following matrix represents the results (the...Ch. 11 - The following data show the pattern of results...Ch. 11 - Explain why the main effects in a factorial study...Ch. 11 - Explain what is meant by the concept that main...Ch. 11 - In Figure 11.5, we show three combinations of main...Ch. 11 - For a two-factor research study with two levels...Ch. 11 - A researcher would like to use a factorial study...Ch. 11 - A two-factor analysis of variance is used to...Ch. 11 - A researcher has demonstrated that a new...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- This item has three questions. The matrix represents the results (means) from a 2 x 2 factorial study. One mean is not given. A represents one factor and B represents the other factor. A1 A2 B1 40 20 B2 30 What value for the missing mean would result in no main effect for factor A? Explain. What value for the missing mean would result in no main effect for factor B? Explain. What value for the missing mean would result in no interaction?Explain.arrow_forwardTo balance inventory at Otto's Optometry, customer Gender and Eye Condition were collected in the data. Make a 2x2 pivot table with Gender in rows and Eye Condition in columns. Customer # Eye Condition Gender 1 Farsighted Male 2 Bifocals Male 3 Nearsighted Male 4 Farsighted Male 5 Nearsighted Female 6 Farsighted Male 7 Farsighted Male 8 Nearsighted Female 9 Nearsighted Male 10 Farsighted Male 11 Bifocals Male 12 Farsighted Female 13 Farsighted Male 14 Farsighted Male 15 Farsighted Male 16 Farsighted Male 17 Nearsighted Male 18 Bifocals Female 19 Farsighted Male 20 Farsighted Male 21 Farsighted Male 22 Bifocals Male 23 Farsighted Female 24 Nearsighted Male 25 Nearsighted Female 26 Bifocals Female 27 Nearsighted Female 28 Farsighted Female 29 Bifocals Male 30 Nearsighted Female 31 Farsighted Male 32 Bifocals Female 33 Farsighted Male 34 Bifocals…arrow_forwardA sports psychologist performed a study of some visualization techniques that she developed to improve athletic performance. She used amateur golfers and amateur tennis players as participants. In her study, 50% of the participants were golfers, and the other 50% were tennis players. (No participant was both a golfer and a tennis player.) The visualization techniques seemed quite helpful for both the golfers and the tennis players: 90% of the golfers reported a solid improvement in their performance after using the visualization techniques, and 85% of the tennis players reported a solid improvement in their performance after using the techniques. Let G denote the event that a randomly chosen participant was a golfer and G denote the event that a randomly chosen participant was a tennis player. Let I denote the event that a randomly chosen participant reported a solid improvement in performance after using the visualization techniques and I denote the event that a randomly chosen…arrow_forward
- A newspaper surveyed companies on the annual amount of money spent on television commercials and the estimated number of people who remember seeing those commercials each week. A soft-drink manufacturer spends $40.1 million a year and estimates 78.6 million people remember the commercials. For a package- delivery service, the budget is $22.9 million for 21.9 million people. A telecommunications company reaches 88.9 million people by spending a whopping $154.9 million. Which matrix below DOES NOT represent this situation? (All value in millions) 40.1 22.9 154.9 C = 78.6 21.9 88.9 21.9 22.9] C = 78.6 40.1 59°F Cloudy 一 一arrow_forwardA fund-raising company is putting together a student kit of candy bars for a school to use in its annual support campaign. To maximize sales, the company will put more of the most popular candy bar sold in an average day in each kit. The company’s research shows that of the five most popular candies, local vending machines sell 100 of Candy A, 14 of Candy B, 50 of Candy C, 6 of Candy D, and 45 of Candy E on an average day. Which candy on average is the most popular candy? Which averaging method did you use?arrow_forwardCan someone help me solve these please ?arrow_forward
- In a famous study done in the 1960s two dolphins, Doris and Buzz, were trained to work together to earn fish. Doris was shown a light underwater. If the light was on steadily, her partner Buzz on the other side of the tank needed to press a button on the right for them to earn fish. If the light was blinking, he needed to press a button on the left. At one point in the study, the researcher hung a canvas in the middle of the tank in such a way that Buzz could not see the light. After looking at the light, Doris "swam near the curtain and began to whistle loudly. Shortly after that Buzz whistled back and then pressed the correct button". (Tintle, Rossman and Chance, MAA Prep Workshop) Of course, getting it right once was not enough to convince the scientists that there was really communication going on. It turned out, that in 15 out of 16 trials the dolphin pushed the correct button. Of course, it is possible that this happened just out of random chance - that the second dolphin just…arrow_forwardIn a famous study done in the 1960s two dolphins, Doris and Buzz, were trained to work together to earn fish. Doris was shown a light underwater. If the light was on steadily, her partner Buzz on the other side of the tank needed to press a button on the right for them to earn fish. If the light was blinking, he needed to press a button on the left. At one point in the study, the researcher hung a canvas in the middle of the tank in such a way that Buzz could not see the light. After looking at the light, Doris “swam near the curtain and began to whistle loudly. Shortly after that Buzz whistled back and then pressed the [correct] button”. (Tintle, Rossman and Chance, MAA Prep Workshop) Of course, getting it right once was not enough to convince the scientists that there was really communication going on. It turned out, that in 15 out of 16 trials the dolphin pushed the correct button. Of course, it is possible that this happened just out of random chance - that the second dolphin just…arrow_forwardIn a town of 10000 families it was found that 40% of families buy newspaper A, 20% family buy newspaper B, 10% family buy newspaper C, 5% family buy newspaper A and B, 3% family buy newspaper B and C and 4% family buy newspaper A and C. If 2% family buy all the newspaper. Find the number of families which buy Number of families which buy all three newspapers. Number of families which buy None of A, B, Carrow_forward
- If you do a 2x4 ANOVA vs 2x3 ANOVA, which statement is correct? A. the 2x4 Anova has more factors thanx2x3 B. the 2x4 ANOVA has more main effects than 2x3 C. the 2x4 ANOVA and the 2x3 ANOVA can both test for exactly three effects D. the 2x4 ANOVA can test for more interactions than the 2x3 ANOVAarrow_forwardAn educational software company wants to compare the effectiveness of its computer animation for teaching biology with that of a textbook presentation. The company gives a biology pretest to each of a group of high school juniors, and then divides them into two groups. One group uses the animation, and the other studies the test. The company retests all students and compares the increase in biology test scores in the two groups b. If the group using the computer animation has a much higher average increase in test scores than the group using the textbook, what conclusions, if any, could the company drawarrow_forwardThe iHub features an array of 3D printers for student use. 3D printers use plastic filament spools to print out plastic parts. The iHub purchases 85% of their filament spools from Amazon, and the rest of their filament spools from Flash Forge. It has been determined that 9% of the filament spools from Amazon are defective, while only 3% of the filament spools from Flash Forge are defective. i) The iHub randomly selects one filament spool from its inventory. What is the probability of it being a defective filament spool? (three decimals) ii) If a filament spool at the iHub is randomly selected and determined to be defective, what is the probability that the filament spool was purchased from Amazon? (three decimals)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Introduction to experimental design and analysis of variance (ANOVA); Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=vSFo1MwLoxU;License: Standard YouTube License, CC-BY