Problem 1E: Complete each of the following statements.
1. As x approaches –2, the value of –3x approaches 6.
Problem 2E: Complete each of the following statements. As x approaches 7_, the value of x2 approaches 5. Problem 3E: Complete each of the following statements. The notation limx4f(x) is read ______. Problem 4E: Complete each of the following statements.
4. The notation is read _____.
Problem 5E: Complete each of the following statements. The notation limx5f(x) is read ______. Problem 6E: Complete each of the following statements.
6. The notation is read ______.
Problem 7E: Complete each of the following statements.
7. The notation _____ is read “the limit, as x approaches... Problem 8E: Complete each of the following statements. The notation ______ is read the limit, as x approaches 3... Problem 9E: Complete each of the following statements. The notation _____ is read the limit as x approaches 5. Problem 10E: Complete each of the following statements. The notation ______ is read the limit as x approaches 12. Problem 11E: For Exercises 11 and 12, consider the function f given by
If a limit does not exist, states... Problem 12E: For Exercises 11 and 12, consider the function f given by
If a limit does not exist, states... Problem 13E: For Exercises 13 and 14, consider the function g given by g(x)={x+6,forx2,12x+1,forx2. If limit does... Problem 14E: For Exercises 13 and 14, consider the function g given by g(x)={x+6,forx2,12x+1,forx2. If limit does... Problem 15E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 16E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 17E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 18E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 19E: For Exercises 1522, use the following graph of F to find each limit. When necessary, state that the... Problem 20E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 21E: For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the... Problem 22E: For Exercises 1522, use the following graph of F to find each limit. When necessary, state that the... Problem 23E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 24E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 25E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 26E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 27E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 28E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 29E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 30E: For Exercises 23-30, use the following graph of G to find each limit. When necessary, state that... Problem 31E: For Exercises 31–40, use the following graph of H to find each limit. When necessary, state that the... Problem 32E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 33E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 34E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 35E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 36E: For Exercises 31–40, use the following graph of H to find each limit. When necessary, state that the... Problem 37E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 38E: For Exercises 31–40, use the following graph of H to find each limit. When necessary, state that the... Problem 39E: For Exercises 31–40, use the following graph of H to find each limit. When necessary, state that the... Problem 40E: For Exercises 3140, use the following graph of H to find each limit. When necessary, state that the... Problem 41E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 42E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 43E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 44E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 45E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 46E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 47E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 48E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 49E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 50E: For Exercises 41-50, use the following graph of f to find each limit. When necessary, state that the... Problem 51E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 52E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 53E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 54E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 55E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 56E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 57E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 58E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 59E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 60E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 61E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 62E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 63E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 64E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 65E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 66E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 67E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 68E: For Exercises 51-68, graph each function and then find the specified limits. When necessary, state... Problem 69E: Business and Economics
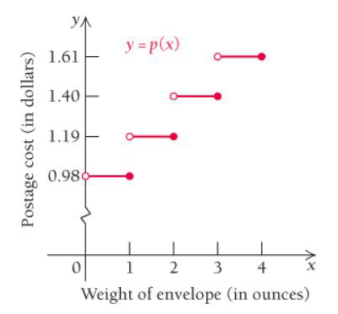
Taxicab fares. In New York City, taxicabs change passengers $2.50 for... Problem 70E: Taxicab fares. In New York City, taxicabs change passengers $2.50 for entering a cab and then $050... Problem 71E: Taxicab fares. In New York City, taxicabs change passengers $2.50 for entering a cab and then $050... Problem 72E: The Postage function. The cost of sending a large envelope via U.S. first-class mail in 2014 was... Problem 73E: The Postage function.
The cost of sending a large envelope via U.S. first-class mail in 2014 was... Problem 74E: The Postage function. The cost of sending a large envelope via U.S. first-class mail in 2014 was... Problem 75E: The Postage function.
The cost of sending a large envelope via U.S. first-class mail in 2014 was... Problem 76E: The Postage function.
The cost of sending a large envelope via U.S. first-class mail in 2014 was... Problem 77E: Tax Rate Schedule. The federal tax rate for single files is given as a percentage of taxable income... Problem 78E: Tax Rate Schedule. The federal tax rate for single files is given as a percentage of taxable income... Problem 79E: Tax Rate Schedule. The federal tax rate for single files is given as a percentage of taxable income... Problem 80E: Tax Rate Schedule.
The federal tax rate for heads of household is given in the graph below.
(Source;... Problem 81E: Tax Rate Schedule.
The federal tax rate for heads of household is given in the graph below.
(Source;... Problem 82E: Tax Rate Schedule.
The federal tax rate for heads of household is given in the graph below.
(Source;... Problem 83E: In Exercises 83-58, fill in each blank so that exists.
83.
Problem 84E: In Exercises 83-58, fill in each blank so that limx2f(x) exists. f(x)={12x+1,forx2,32x+,forx2 Problem 85E: In Exercises 83-58, fill in each blank so that limx2f(x) exists. f(x)={x29,forx2,x2+,forx2 Problem 86E: Graph the function f given by f(x)={3,forx=2,x2forx2. Use GRAPH and TRACE to find each of the... Problem 87E: In Exercises 87-89, use GRAFH and TRACE to find each limit. When necessary, state that the limit... Problem 88E: In Exercises 87-89, use GRAFH and TRACE to find each limit. When necessary, state that the limit... Problem 89E: In Exercises 87-89, use GRAFH and TRACE to find each limit. When necessary, state that the limit... format_list_bulleted


 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





