Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
10th Edition
ISBN: 9781337278461
Author: Ron Larson
Publisher: Cengage Learning
bartleby

Concept explainers

Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 …
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experime…
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.1, Problem 68E

Speed of a Bicycle

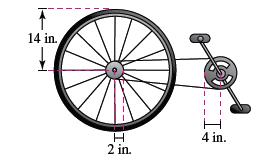
The radii of the pedal sprocket, the wheel sprocket,and the wheel of the bicycle in the figure are 4 inches, 2 inches, and 14 inches, respectively. A cyclist pedals at a rate of 1 revolution per second.

Chapter 1.1, Problem 68E, Speed of a Bicycle The radii of the pedal sprocket, the wheel sprocket,and the wheel of the bicycle , example 1

a Find the speed of the bicycle in feet per second and miles per hour.

b Use your result from part (a) to write a function for the distance d (in miles) a cyclist travels in terms of the number n of revolutions of the pedal sprocket.

( c ) Write a function for the distance d (in miles) a cyclist travels in terms of the time t (in seconds). Compare this function with the function from part (b).

Chapter 1.1, Problem 68E, Speed of a Bicycle The radii of the pedal sprocket, the wheel sprocket,and the wheel of the bicycle , example 2

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 1.1, Problem 67E
Next
Chapter 1.1, Problem 69E
Students have asked these similar questions
Hi can you find the answers to unit 21 review questions in Delmar's standard textbook of electricity
pls exact values
Find the polar representations of a point which has -л<О≤л and is symmetrical to the given point with respect to the origin. (√2.- 1/1) π 4

Chapter 1 Solutions

Trigonometry (MindTap Course List)

Ch. 1.1 - Determine two coterminal angles (one positive and...Ch. 1.1 - Prob. 2ECPCh. 1.1 - Convert each degree measure to radian measure as a...Ch. 1.1 - Prob. 4ECPCh. 1.1 - A circle has a radius of 27 inches. Find the...Ch. 1.1 - The second hand of a clock is 8 centimeters long....Ch. 1.1 - The circular blade on a saw has a radius of 4...Ch. 1.1 - Prob. 8ECPCh. 1.1 - Fill in the blanks. Two angles that have the same...Ch. 1.1 - Prob. 2E
Ch. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Fill in the blanks. The ________ speed of a...Ch. 1.1 - Fill in the blanks. The area A of a sector of a...Ch. 1.1 - Estimating an Angle In Exercises 7-10, estimate...Ch. 1.1 - Estimating an Angle In Exercises 7-10, estimate...Ch. 1.1 - Estimating an Angle In Exercises 7-10, estimate...Ch. 1.1 - Estimating an Angle In Exercises 7-10, estimate...Ch. 1.1 - Determining Quadrants In Exercises 11 and 12,...Ch. 1.1 - Determining Quadrants In Exercises 11 and 12,...Ch. 1.1 - Sketching Angles In Exercises 13 and 14, sketch...Ch. 1.1 - Sketching Angles In Exercises 13 and 14, sketch...Ch. 1.1 - Finding Coterminal Angles In Exercises 15 and 16,...Ch. 1.1 - Finding Coterminal Angles In Exercises 15 and 16,...Ch. 1.1 - Complementary and Supplementary Angles In...Ch. 1.1 - Complementary and Supplementary Angles In...Ch. 1.1 - Complementary and Supplementary Angles In...Ch. 1.1 - Complementary and Supplementary Angles In...Ch. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Determining Quadrants In Exercises 25 and 26,...Ch. 1.1 - Sketching Angles In Exercises 27 and 28, sketch...Ch. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Converting from Degrees to Radians In Exercises 35...Ch. 1.1 - Converting from Degrees to Radians In Exercises 35...Ch. 1.1 - Converting from Radians to Degrees In Exercises 37...Ch. 1.1 - Converting from Radians to Degrees In Exercises 37...Ch. 1.1 - Prob. 39ECh. 1.1 - Converting from Degrees to Radians In Exercises...Ch. 1.1 - Converting from Degrees to Radians In Exercises...Ch. 1.1 - Converting from Degrees to Radians In Exercises...Ch. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Converting from Radians to Degrees In Exercises...Ch. 1.1 - Prob. 46ECh. 1.1 - Converting to Decimal Degree Form In Exercises 47...Ch. 1.1 - Converting to Decimal Degree Form In Exercises 47...Ch. 1.1 - Converting to DM'S Form In Exercises 49 and 50,...Ch. 1.1 - Prob. 50ECh. 1.1 - Finding Arc Length In Exercises 51 and 52, find...Ch. 1.1 - Prob. 52ECh. 1.1 - Finding the Central Angle In Exercises 53 and 54,...Ch. 1.1 - Finding the Central Angle In Exercises 53 and 54,...Ch. 1.1 - Finding the Central Angle In Exercises 55 and 56,...Ch. 1.1 - Finding the Central Angle In Exercises 55 and 56,...Ch. 1.1 - Area of a Sector of a Circle In Exercises 57 and...Ch. 1.1 - Area of a Sector of a Circle In Exercises 57 and...Ch. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Instrumentation The pointer on a voltmeter is 6...Ch. 1.1 - Linear and Angular Speed A 714 -inch circular...Ch. 1.1 - Linear and Angular Speed A carousel with 50-foot...Ch. 1.1 - Linear and Angular Speed A Blu-ray disc is...Ch. 1.1 - Linear and Angular Speed A computerized spin...Ch. 1.1 - Speed of a Bicycle The radii of the pedal...Ch. 1.1 - Area A sprinkler on a golf green is set to spray...Ch. 1.1 - Area A car’s rear windshield wiper rotates 125°....Ch. 1.1 - Prob. 71ECh. 1.1 - True or False? In Exercises 71-74, determine...Ch. 1.1 - True or False? In Exercises 71–74, determine...Ch. 1.1 - True or False? In Exercises 71–74, determine...Ch. 1.1 - Writing When the radius of a circle increases and...Ch. 1.1 - Prob. 76ECh. 1.1 - Prob. 77ECh. 1.1 - Prob. 78ECh. 1.1 - Prob. 79ECh. 1.2 - Prob. 1ECPCh. 1.2 - Prob. 2ECPCh. 1.2 - Prob. 3ECPCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Evaluating Sine, Cosine, and Tangent In Exercises...Ch. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Evaluating Sine, Cosine, and Tangent In Exercises...Ch. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Using Period to Evaluate Sine and Cosine In...Ch. 1.2 - Using Period to Evaluate Sine and Cosine In...Ch. 1.2 - Using Period to Evaluate Sine and Cosine In...Ch. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Using the Value of a Function In Exercises 37-42,...Ch. 1.2 - Using the Value of a Function In Exercises 37–42,...Ch. 1.2 - Using the Value of a Function In Exercises 37-42,...Ch. 1.2 - Using the Value of a Function In Exercises 37–42,...Ch. 1.2 - Using the Value of a Function In Exercises 37–42,...Ch. 1.2 - Using the Value of a Function In Exercises 37–42,...Ch. 1.2 - Using a Calculator In Exercises 43-48, use a...Ch. 1.2 - Using a Calculator In Exercises 43-48, use a...Ch. 1.2 - Using a Calculator In Exercises 43-48, use a...Ch. 1.2 - Using a Calculator In Exercises 43-48, use a...Ch. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Harmonic Motion The displacement from equilibrium...Ch. 1.2 - The displacement from equilibrium of an...Ch. 1.2 - True of False? In Exercises 51–54, determine...Ch. 1.2 - Prob. 52ECh. 1.2 - True of False? In Exercises 51–54, determine...Ch. 1.2 - True of False? In Exercises 51–54, determine...Ch. 1.2 - Conjecture Let (x1,y1) and (x2,y2) be points on...Ch. 1.2 - Using the Unit Circle Use the unit circle to...Ch. 1.2 - Error Analysis Describe the error. Your classmate...Ch. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - HOW DO YOU SEE IT? Use the figure below. (a) Are...Ch. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.3 - Use the triangle below to find the values of the...Ch. 1.3 - Find the values of cot45,sec45, and csc45.Ch. 1.3 - Use the equilateral triangle shown in Figure 1.21...Ch. 1.3 - Use a calculator to evaluate csc343036.Ch. 1.3 - Let be an acute angle such that cos =0.96. Find...Ch. 1.3 - Prob. 6ECPCh. 1.3 - Prob. 7ECPCh. 1.3 - The angle of elevation to the top of a flagpole at...Ch. 1.3 - Prob. 9ECPCh. 1.3 - Prob. 10ECPCh. 1.3 - Match each trigonometric function with its right...Ch. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Prob. 17ECh. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Prob. 19ECh. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions In Exercises...Ch. 1.3 - Evaluating Trigonometric Functions of 30,45, 60 In...Ch. 1.3 - Prob. 24ECh. 1.3 - Evaluating Trigonometric Functions of 30,45, and...Ch. 1.3 - Evaluating Trigonometric Functions of 30,45, and...Ch. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Using a Calculator In Exercises 29-36, use a...Ch. 1.3 - Using a Calculator In Exercises 29-36, use a...Ch. 1.3 - Using a Calculator In Exercises 29-36, use a...Ch. 1.3 - Prob. 34ECh. 1.3 - Using a Calculator In Exercises 29-36, use a...Ch. 1.3 - Using a Calculator In Exercises 29-36, use a...Ch. 1.3 - Applying Trigonometric Identities In Exercises...Ch. 1.3 - Applying Trigonometric Identities In Exercises...Ch. 1.3 - Applying Trigonometric Identities In Exercises...Ch. 1.3 - Applying Trigonometric Identities In Exercises...Ch. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Using Trigonometric Identities In Exercises 43-52,...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Special Angles of a Triangle In Exercises...Ch. 1.3 - Finding Side Lengths of a Triangle In Exercises...Ch. 1.3 - Finding Side Lengths of a Triangle In Exercises...Ch. 1.3 - Finding Side Lengths of a Triangle In Exercises...Ch. 1.3 - Finding Side Lengths of a Triangle In Exercises...Ch. 1.3 - Empire State Building You are standing 45 meters...Ch. 1.3 - Height of a Tower A six-foot person walks from the...Ch. 1.3 - Angle of Elevation You are skiing down a mountain...Ch. 1.3 - Biology A biologist wants to know the width w of a...Ch. 1.3 - Guy Wire A guy wire runs from the ground to a cell...Ch. 1.3 - Height of a Mountain In traveling across flat...Ch. 1.3 - Prob. 69ECh. 1.3 - Machine Shop Calculations A tapered shaft has a...Ch. 1.3 - Geometry Use a compass to sketch a quarter of a...Ch. 1.3 - A 20 meter line is used to tether a helium-filled...Ch. 1.3 - Johnstown Inclined Plane The Johnstown Inclined...Ch. 1.3 - Prob. 74ECh. 1.3 - Prob. 75ECh. 1.3 - Prob. 76ECh. 1.3 - Prob. 77ECh. 1.3 - True or False? In Exercises 75-80, determine...Ch. 1.3 - True or False? In Exercises 75-80, determine...Ch. 1.3 - True or False? In Exercises 75-80, determine...Ch. 1.3 - Think About It You are given the value of tan. Is...Ch. 1.3 - HOW DO YOU SEE IT? Use the figure below....Ch. 1.3 - Think About It Complete the table. (a) Is or sin...Ch. 1.3 - Think About It Complete the table. (a) Discuss the...Ch. 1.4 - Let 2,3 be a point on the terminal side of . Find...Ch. 1.4 - Given sin =45 and tan 0, find cos and tan .Ch. 1.4 - Evaluate the sine and cotangent functions at the...Ch. 1.4 - Prob. 4ECPCh. 1.4 - Prob. 5ECPCh. 1.4 - Prob. 6ECPCh. 1.4 - Prob. 7ECPCh. 1.4 - Fill in the blanks. In Exercises 16, let be an...Ch. 1.4 - Fill in the blanks. In Exercises 16, let be an...Ch. 1.4 - Fill in the blanks. In Exercises 16, let be an...Ch. 1.4 - Fill in the blanks. In Exercises 16, let be an...Ch. 1.4 - Fill in the blanks. In Exercises 16, let be an...Ch. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - In Exercises 13-18, the point is on the terminal...Ch. 1.4 - In Exercises 13-18, the point is on the terminal...Ch. 1.4 - In Exercises 13-18, the point is on the terminal...Ch. 1.4 - In Exercises 13-18, the point is on the terminal...Ch. 1.4 - In Exercises 13-18, the point is on the terminal...Ch. 1.4 - Prob. 18ECh. 1.4 - Determining a Quadrant In Exercises 19-22,...Ch. 1.4 - Determining a Quadrant In Exercises 19-22,...Ch. 1.4 - Determining a Quadrant In Exercises 19-22,...Ch. 1.4 - Determining a Quadrant In Exercises 19-22,...Ch. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - Prob. 31ECh. 1.4 - Evaluating Trigonometric Functions In Exercises...Ch. 1.4 - An Angle Formed by a Line Through the Origin In...Ch. 1.4 - An Angle Formed by a Line Through the Origin In...Ch. 1.4 - An Angle Formed by a Line Through the Origin In...Ch. 1.4 - An Angle Formed by a Line Through the Origin In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Trigonometric Function of a Quadrantal Angle In...Ch. 1.4 - Finding a Reference Angle In Exercises 47-54, find...Ch. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Using a Trigonometric Identity In Exercises 69-74,...Ch. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.4 - Prob. 85ECh. 1.4 - Prob. 86ECh. 1.4 - Prob. 87ECh. 1.4 - Prob. 88ECh. 1.4 - Prob. 89ECh. 1.4 - Prob. 90ECh. 1.4 - Solving for In Exercises 91-96, find two...Ch. 1.4 - Prob. 92ECh. 1.4 - Prob. 93ECh. 1.4 - Prob. 94ECh. 1.4 - Prob. 95ECh. 1.4 - Prob. 96ECh. 1.4 - Prob. 97ECh. 1.4 - Prob. 98ECh. 1.4 - Prob. 99ECh. 1.4 - Sales A company that produces snowboards forecasts...Ch. 1.4 - Prob. 101ECh. 1.4 - Prob. 102ECh. 1.4 - Prob. 103ECh. 1.4 - Prob. 104ECh. 1.4 - Prob. 105ECh. 1.4 - Prob. 106ECh. 1.5 - Sketch the graph of y=2cosx on the interval 2,92.Ch. 1.5 - Prob. 2ECPCh. 1.5 - Prob. 3ECPCh. 1.5 - Prob. 4ECPCh. 1.5 - Prob. 5ECPCh. 1.5 - Prob. 6ECPCh. 1.5 - Prob. 7ECPCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Finding the Period and Amplitude In Exercises...Ch. 1.5 - Finding the Period and Amplitude In Exercises...Ch. 1.5 - Finding the Period and Amplitude In Exercises...Ch. 1.5 - Prob. 8ECh. 1.5 - Finding the Period and Amplitude In Exercises...Ch. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Finding the Period and Amplitude In Exercises...Ch. 1.5 - Describing the Relationship Between Graphs In...Ch. 1.5 - Prob. 14ECh. 1.5 - Describing the Relationship Between Graphs In...Ch. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Describing the Relationship Between Graphs In...Ch. 1.5 - Describing the Relationship Between Graphs In...Ch. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Sketching the Graph of a Sine or Cosine Function...Ch. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Sketching the Graph of a Sine or Cosine Function...Ch. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Sketching the Graph of a Sine or Cosine Function...Ch. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Graphical Reasoning In Exercises 65-68, find a and...Ch. 1.5 - Graphical Reasoning In Exercises 65-68, find a and...Ch. 1.5 - Prob. 67ECh. 1.5 - Graphical Reasoning In Exercises 65-68, find a and...Ch. 1.5 - Graphical Reasoning In Exercises 69-72, find a,b,...Ch. 1.5 - Graphical Reasoning In Exercises 69-72, find a,b,...Ch. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1.5 - Prob. 77ECh. 1.5 - Prob. 78ECh. 1.5 - Prob. 79ECh. 1.5 - For a person at rest, the velocity v (in liters...Ch. 1.5 - Prob. 81ECh. 1.5 - Piano Tuning When tuning a piano, a technician...Ch. 1.5 - Astronomy The table shows the percent y (in...Ch. 1.5 - Meteorology The table shows the maximum daily high...Ch. 1.5 - Ferris Wheel The height h (in feet) above ground...Ch. 1.5 - Fuel Consumption The daily consumption C (in...Ch. 1.5 - Prob. 87ECh. 1.5 - True or False? In Exercises 87-89, determine...Ch. 1.5 - True or False? In Exercises 87-89, determine...Ch. 1.5 - Prob. 90ECh. 1.5 - Prob. 91ECh. 1.5 - Prob. 92ECh. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - Prob. 95ECh. 1.6 - Prob. 1ECPCh. 1.6 - Prob. 2ECPCh. 1.6 - Prob. 3ECPCh. 1.6 - Prob. 4ECPCh. 1.6 - Prob. 5ECPCh. 1.6 - Prob. 6ECPCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Solving a Trigonometric Equation In Exercises...Ch. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.6 - Prob. 69ECh. 1.6 - Prob. 70ECh. 1.6 - Prob. 71ECh. 1.6 - Prob. 72ECh. 1.6 - Prob. 73ECh. 1.6 - Prob. 74ECh. 1.6 - Prob. 75ECh. 1.6 - Prob. 76ECh. 1.6 - Prob. 77ECh. 1.6 - Prob. 78ECh. 1.6 - Prob. 79ECh. 1.6 - Prob. 80ECh. 1.6 - Prob. 81ECh. 1.6 - Prob. 82ECh. 1.6 - Meteorology The normal monthly high temperatures H...Ch. 1.6 - Sales The projected monthly sales S (in thousands...Ch. 1.6 - Prob. 85ECh. 1.6 - Distance A plane flying at an altitude of 7 miles...Ch. 1.6 - Prob. 87ECh. 1.6 - Prob. 88ECh. 1.6 - Prob. 89ECh. 1.6 - Prob. 90ECh. 1.6 - Prob. 91ECh. 1.6 - Prob. 92ECh. 1.6 - Prob. 93ECh. 1.6 - Prob. 94ECh. 1.7 - If possible, find the exact value of each...Ch. 1.7 - Prob. 2ECPCh. 1.7 - Prob. 3ECPCh. 1.7 - Use a calculator to approximate the value of each...Ch. 1.7 - Prob. 5ECPCh. 1.7 - Prob. 6ECPCh. 1.7 - Prob. 7ECPCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Fill in the blanks....Ch. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - Prob. 36ECh. 1.7 - Prob. 37ECh. 1.7 - Finding Missing Coordinates In Exercises 37 and...Ch. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Using an Inverse Trigonometric Function In...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Using Inverse Properties In Exercises 45-50, find...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Evaluating a Composition of Functions In Exercises...Ch. 1.7 - Prob. 63ECh. 1.7 - Prob. 64ECh. 1.7 - Prob. 65ECh. 1.7 - Prob. 66ECh. 1.7 - Prob. 67ECh. 1.7 - Prob. 68ECh. 1.7 - Prob. 69ECh. 1.7 - Prob. 70ECh. 1.7 - Writing an Expression In Exercises 63-72, write an...Ch. 1.7 - Prob. 72ECh. 1.7 - Prob. 73ECh. 1.7 - Prob. 74ECh. 1.7 - Prob. 75ECh. 1.7 - Prob. 76ECh. 1.7 - Prob. 77ECh. 1.7 - Prob. 78ECh. 1.7 - Prob. 79ECh. 1.7 - Prob. 80ECh. 1.7 - Prob. 81ECh. 1.7 - Prob. 82ECh. 1.7 - Prob. 83ECh. 1.7 - Prob. 84ECh. 1.7 - Prob. 85ECh. 1.7 - Prob. 86ECh. 1.7 - Prob. 87ECh. 1.7 - Prob. 88ECh. 1.7 - Prob. 89ECh. 1.7 - Prob. 90ECh. 1.7 - Prob. 91ECh. 1.7 - Prob. 92ECh. 1.7 - Prob. 93ECh. 1.7 - Prob. 94ECh. 1.7 - Prob. 95ECh. 1.7 - Prob. 96ECh. 1.7 - Prob. 97ECh. 1.7 - Prob. 98ECh. 1.7 - Docking a Boat A boat is pulled in by means of a...Ch. 1.7 - A television camera at ground level films the...Ch. 1.7 - Granular Angle of Repose Different types of...Ch. 1.7 - Prob. 102ECh. 1.7 - Photography A photographer takes a picture of a...Ch. 1.7 - Prob. 104ECh. 1.7 - Police Patrol A police car with its spotlight on...Ch. 1.7 - Prob. 106ECh. 1.7 - Prob. 107ECh. 1.7 - Prob. 108ECh. 1.7 - Prob. 109ECh. 1.7 - Prob. 110ECh. 1.7 - Prob. 111ECh. 1.7 - Prob. 112ECh. 1.7 - Prob. 113ECh. 1.7 - Prob. 114ECh. 1.7 - Prob. 115ECh. 1.7 - Prob. 116ECh. 1.7 - Prob. 117ECh. 1.7 - Prob. 118ECh. 1.7 - Prob. 119ECh. 1.7 - Evaluating an Inverse Trigonometric Function In...Ch. 1.7 - Prob. 121ECh. 1.7 - Prob. 122ECh. 1.7 - Prob. 123ECh. 1.7 - Prob. 124ECh. 1.7 - Calculators and Inverse Trigonometric Functions In...Ch. 1.7 - Calculators and Inverse Trigonometric Functions In...Ch. 1.7 - Prob. 127ECh. 1.7 - Think About It Use a graphing utility to graph the...Ch. 1.7 - Prob. 129ECh. 1.7 - Prob. 130ECh. 1.8 - Solve the right triangle shown at the right for...Ch. 1.8 - Prob. 2ECPCh. 1.8 - At a point 65 feet from the base of a church, the...Ch. 1.8 - From the time a small airplane is 100 feet high...Ch. 1.8 - Prob. 5ECPCh. 1.8 - Prob. 6ECPCh. 1.8 - Prob. 7ECPCh. 1.8 - Fill in the blanks. A measures the acute angle...Ch. 1.8 - A point that moves on a coordinate line is in...Ch. 1.8 - Fill in the blanks. The time for one complete...Ch. 1.8 - The number of cycles per second of a point in...Ch. 1.8 - Solving a Right Triangle In Exercises 5-12, solve...Ch. 1.8 - Solving a Right Triangle In Exercises 5-12, solve...Ch. 1.8 - Solving a Right Triangle In Exercises 5-12, solve...Ch. 1.8 - Solving a Right Triangle In Exercises 5-12, solve...Ch. 1.8 - Prob. 9ECh. 1.8 - Prob. 10ECh. 1.8 - Prob. 11ECh. 1.8 - Solving a Right Triangle In Exercises 5-12, solve...Ch. 1.8 - Finding an Altitude In Exercises 13-16, find the...Ch. 1.8 - Prob. 14ECh. 1.8 - Finding an Altitude In Exercises 13-16, find the...Ch. 1.8 - Prob. 16ECh. 1.8 - Prob. 17ECh. 1.8 - Prob. 18ECh. 1.8 - Prob. 19ECh. 1.8 - Prob. 20ECh. 1.8 - Height At a point 50 feet from the base of a...Ch. 1.8 - Distance An observer in a lighthouse 350 feet...Ch. 1.8 - Distance A passenger in an airplane at an altitude...Ch. 1.8 - Angle of Elevation The height of an outdoor...Ch. 1.8 - Angle of Elevation An engineer designs a 75-foot...Ch. 1.8 - Angle of Depression A cellular telephone tower...Ch. 1.8 - Angle of Depression A Global Positioning System...Ch. 1.8 - Height You are holding one of the tethers attached...Ch. 1.8 - Prob. 29ECh. 1.8 - The designers of a water park have sketched a...Ch. 1.8 - Speed Enforcement A police department has set up a...Ch. 1.8 - Airplane Ascent During takeoff, an airplane’s...Ch. 1.8 - Air Navigation An airplane flying at 550 miles per...Ch. 1.8 - Prob. 34ECh. 1.8 - Prob. 35ECh. 1.8 - Prob. 36ECh. 1.8 - Prob. 37ECh. 1.8 - Prob. 38ECh. 1.8 - Surveying A surveyor wants to find the distance...Ch. 1.8 - Location of a Fire tower A is 30 kilometers due...Ch. 1.8 - Prob. 41ECh. 1.8 - Prob. 42ECh. 1.8 - Geometry Find the length of the sides of a regular...Ch. 1.8 - Prob. 44ECh. 1.8 - Simple Harmonic Motion In Exercises 45-48, find a...Ch. 1.8 - Simple Harmonic Motion In Exercises 45-48, find a...Ch. 1.8 - Prob. 47ECh. 1.8 - Prob. 48ECh. 1.8 - Tuning Fork A point on the end of a tuning fork...Ch. 1.8 - Prob. 50ECh. 1.8 - Prob. 51ECh. 1.8 - Prob. 52ECh. 1.8 - Prob. 53ECh. 1.8 - Simple Harmonic Motion In Exercises 51-54, for the...Ch. 1.8 - Oscillation of a Spring A ball that is bobbing up...Ch. 1.8 - Hours of Daylight The numbers of hours H of...Ch. 1.8 - Sales The table shows the average sales S (in...Ch. 1.8 - HOW DO YOU SEE IT? The graph below shows the...Ch. 1.8 - True or False? In Exercises 59 and 60, determine...Ch. 1.8 - Prob. 60ECh. 1 - Using Radian or Degree Measure In Exercises 1-4,...Ch. 1 - Using Radian or Degree Measure In Exercises 1-4,...Ch. 1 - Using Radian or Degree Measure In Exercises 1-4,...Ch. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Phonograph Phonograph records are vinyl discs that...Ch. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Railroad Grade A train travels 3.5 kilometers on a...Ch. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Sketching the Graph of a Sine or Cosine Function...Ch. 1 - Prob. 65RECh. 1 - Sketching the Graph of a Sine or Cosine Function...Ch. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Meteorology The times S of sunset (Greenwich Mean...Ch. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Calculators and Inverse Trigonometric Functions In...Ch. 1 - Calculators and Inverse Trigonometric Functions In...Ch. 1 - Calculators and Inverse Trigonometric Functions In...Ch. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Evaluating a Composition of Functions In Exercises...Ch. 1 - Evaluating a Composition of Functions In Exercises...Ch. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Writing an Expression In Exercises 91 and 92,...Ch. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Air Navigation From city A to city B, a plane...Ch. 1 - Prob. 96RECh. 1 - True or False? In Exercises 97 and 98, determine...Ch. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - Writing When graphing the sine and cosine...Ch. 1 - Graphical Reasoning Use the formulas for the area...Ch. 1 - Take this test as you would take a test in class....Ch. 1 - Prob. 2TCh. 1 - Take this test as you would take a test in class....Ch. 1 - Take this test as you would take a test in class....Ch. 1 - Take this test as you would take a test in class....Ch. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - Prob. 9TCh. 1 - In Exercises 9 and 10, find the exact values of...Ch. 1 - Prob. 11TCh. 1 - In Exercises 11-13, sketch the graph of the...Ch. 1 - In Exercises 11-13, sketch the graph of the...Ch. 1 - In Exercises 14 and 15, use a graphing utility to...Ch. 1 - In Exercises 14 and 15, use a graphing utility to...Ch. 1 - Prob. 16TCh. 1 - Prob. 17TCh. 1 - Sketch the graph of the function fx=2arcsin12x.Ch. 1 - An airplane is 90 miles south and 110 miles east...Ch. 1 - A ball on a spring starts at its lowest point of 6...Ch. 1 - Prob. 1PSCh. 1 - Prob. 2PSCh. 1 - Prob. 3PSCh. 1 - Periodic Function The function f is periodic, with...Ch. 1 - Surveying A surveyor in a helicopter is...Ch. 1 - Similar Triangles and Trigonometric Functions Use...Ch. 1 - Prob. 7PSCh. 1 - Prob. 8PSCh. 1 - Blood Pressure The pressure P (in millimeters of...Ch. 1 - Biorhythms A popular theory that attempts to...Ch. 1 - Prob. 11PSCh. 1 - Prob. 12PSCh. 1 - Refraction When you stand in shallow water and...Ch. 1 - Prob. 14PS
Knowledge Booster
Background pattern image
Trigonometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY