Skip to main content

High School Math Calculus CALCULUS-W/XL ACCESS

The graph of f .

The graph of f .

Solution Summary: The graph of f is shown below. The left and right hand limits at those points are not equal.

CALCULUS-W/XL ACCESS

CALCULUS-W/XL ACCESS

6th Edition

ISBN: 9781418300197

Author: Finney

Publisher: PEARSON

See similar textbooks

Question

Chapter 1.1, Problem 64E

(a)

To determine

To find: The graph of f .

(a)

Expert Solution

Answer to Problem 64E

The graph is shown:

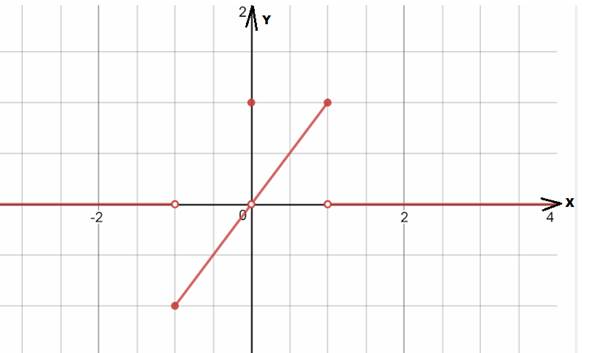
CALCULUS-W/XL ACCESS , Chapter 1.1, Problem 64E , additional homework tip 1

Explanation of Solution

Given information: The function is:

f(x)=x,−1≤x<0, or 0<x≤11,x=00,x−1, or x1

Graph:

The graph of the given function is shown below:

CALCULUS-W/XL ACCESS , Chapter 1.1, Problem 64E , additional homework tip 2

(b)

To determine

To find: The points of c in the domain of f does lim x→c f(x) exists.

(b)

Expert Solution

Answer to Problem 64E

c∈(−∞,1)∪(−1,1)∪(1,∞)

Explanation of Solution

Given information: The function is:

f(x)=x,−1≤x<0, or 0<x≤11,x=00,x−1, or x1

Calculation:

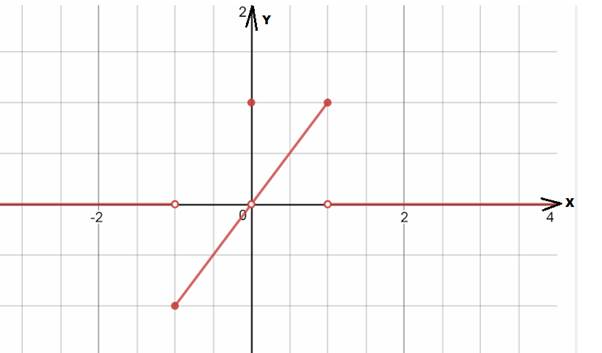
The domain of the function is (−∞,∞) .

The limit does not exists at

x=−1 x=1

Since the left and right hand limits at those points are not equal.

Therefore the required the limits exists for all c∈(−∞,1)∪(−1,1)∪(1,∞) .

(c)

To determine

To find: The points that c does only the left hand limits exits.

(c)

Expert Solution

Answer to Problem 64E

None.

Explanation of Solution

Given information: The function is:

f(x)=x,−1≤x<0, or 0<x≤11,x=00,x−1, or x1

Calculation:

The limit is evident from 64b at all places other than x=−1 x=1 .

However, whether or not they are equal, there are left- and right-hand limitations at certain locations. Thus, there are points where only the left-hand limit is present, such as at,0no points.

(d)

To determine

To find: The points that c does only the right hand limits exits.

(d)

Expert Solution

Answer to Problem 64E

None.

Explanation of Solution

Given information: The function is:

f(x)=x,−1≤x<0, or 0<x≤11,x=00,x−1, or x1

Calculation:

The limit is evident from 64b at all places other than x=−1 x=1 .

However, whether or not they are equal, there are left- and right-hand limitations at certain locations. There are therefore "no points" where the right-hand limit is the only one that exists.

Chapter 1.1, Problem 63E

Chapter 1.1, Problem 65E

Chapter 1 Solutions

CALCULUS-W/XL ACCESS

Ch. 1.1 - Prob. 1QR Ch. 1.1 - Prob. 2QR Ch. 1.1 - Prob. 3QR Ch. 1.1 - Prob. 4QR Ch. 1.1 - Prob. 5QR Ch. 1.1 - Prob. 6QR Ch. 1.1 - Prob. 7QR Ch. 1.1 - Prob. 8QR Ch. 1.1 - Prob. 9QR Ch. 1.1 - Prob. 10QR

Ch. 1.1 - Prob. 1E Ch. 1.1 - Prob. 2E Ch. 1.1 - Prob. 3E Ch. 1.1 - Prob. 4E Ch. 1.1 - Prob. 5E Ch. 1.1 - Prob. 6E Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E Ch. 1.1 - Prob. 11E Ch. 1.1 - Prob. 12E Ch. 1.1 - Prob. 13E Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Prob. 17E Ch. 1.1 - Prob. 18E Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Prob. 49E Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - Prob. 58E Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.1 - Prob. 64E Ch. 1.1 - Prob. 65E Ch. 1.1 - Prob. 66E Ch. 1.1 - Prob. 67E Ch. 1.1 - Prob. 68E Ch. 1.1 - Prob. 69E Ch. 1.1 - Prob. 70E Ch. 1.1 - Prob. 71E Ch. 1.1 - Prob. 72E Ch. 1.1 - Prob. 73E Ch. 1.1 - Prob. 74E Ch. 1.1 - Prob. 75E Ch. 1.1 - Prob. 76E Ch. 1.1 - Prob. 77E Ch. 1.1 - Prob. 78E Ch. 1.1 - Prob. 79E Ch. 1.1 - Prob. 80E Ch. 1.2 - Prob. 1QR Ch. 1.2 - Prob. 2QR Ch. 1.2 - Prob. 3QR Ch. 1.2 - Prob. 4QR Ch. 1.2 - Prob. 5QR Ch. 1.2 - Prob. 6QR Ch. 1.2 - Prob. 7QR Ch. 1.2 - Prob. 8QR Ch. 1.2 - Prob. 9QR Ch. 1.2 - Prob. 10QR Ch. 1.2 - Prob. 1E Ch. 1.2 - Prob. 2E Ch. 1.2 - Prob. 3E Ch. 1.2 - Prob. 4E Ch. 1.2 - Prob. 5E Ch. 1.2 - Prob. 6E Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - Prob. 12E Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Prob. 15E Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.2 - Prob. 27E Ch. 1.2 - Prob. 28E Ch. 1.2 - Prob. 29E Ch. 1.2 - Prob. 30E Ch. 1.2 - Prob. 31E Ch. 1.2 - Prob. 32E Ch. 1.2 - Prob. 33E Ch. 1.2 - Prob. 34E Ch. 1.2 - Prob. 35E Ch. 1.2 - Prob. 36E Ch. 1.2 - Prob. 37E Ch. 1.2 - Prob. 38E Ch. 1.2 - Prob. 39E Ch. 1.2 - Prob. 40E Ch. 1.2 - Prob. 41E Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - Prob. 44E Ch. 1.2 - Prob. 45E Ch. 1.2 - Prob. 46E Ch. 1.2 - Prob. 47E Ch. 1.2 - Prob. 48E Ch. 1.2 - Prob. 49E Ch. 1.2 - Prob. 50E Ch. 1.2 - Prob. 51E Ch. 1.2 - Prob. 52E Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Prob. 63E Ch. 1.2 - Prob. 64E Ch. 1.2 - Prob. 65E Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 1QQ Ch. 1.2 - Prob. 2QQ Ch. 1.2 - Prob. 3QQ Ch. 1.2 - Prob. 4QQ Ch. 1.3 - Prob. 1QR Ch. 1.3 - Prob. 2QR Ch. 1.3 - Prob. 3QR Ch. 1.3 - Prob. 4QR Ch. 1.3 - Prob. 5QR Ch. 1.3 - Prob. 6QR Ch. 1.3 - Prob. 7QR Ch. 1.3 - Prob. 8QR Ch. 1.3 - Prob. 9QR Ch. 1.3 - Prob. 10QR Ch. 1.3 - Prob. 1E Ch. 1.3 - Prob. 2E Ch. 1.3 - Prob. 3E Ch. 1.3 - Prob. 4E Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - Prob. 25E Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Prob. 52E Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - Prob. 55E Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - Prob. 58E Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.4 - Prob. 1QR Ch. 1.4 - Prob. 2QR Ch. 1.4 - Prob. 3QR Ch. 1.4 - Prob. 4QR Ch. 1.4 - Prob. 5QR Ch. 1.4 - Prob. 6QR Ch. 1.4 - Prob. 7QR Ch. 1.4 - Prob. 8QR Ch. 1.4 - Prob. 9QR Ch. 1.4 - Prob. 10QR Ch. 1.4 - Prob. 1E Ch. 1.4 - Prob. 2E Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.4 - Prob. 39E Ch. 1.4 - Prob. 40E Ch. 1.4 - Prob. 41E Ch. 1.4 - Prob. 42E Ch. 1.4 - Prob. 43E Ch. 1.4 - Prob. 44E Ch. 1.4 - Prob. 45E Ch. 1.4 - Prob. 46E Ch. 1.4 - Prob. 47E Ch. 1.4 - Prob. 48E Ch. 1.4 - Prob. 49E Ch. 1.4 - Prob. 50E Ch. 1.4 - Prob. 51E Ch. 1.4 - Prob. 52E Ch. 1.4 - Prob. 53E Ch. 1.4 - Prob. 54E Ch. 1.4 - Prob. 55E Ch. 1.4 - Prob. 56E Ch. 1.4 - Prob. 57E Ch. 1.4 - Prob. 1QQ Ch. 1.4 - Prob. 2QQ Ch. 1.4 - Prob. 3QQ Ch. 1.4 - Prob. 4QQ Ch. 1 - Prob. 1RWDT Ch. 1 - Prob. 2RWDT Ch. 1 - Prob. 3RWDT Ch. 1 - Prob. 4RWDT Ch. 1 - Prob. 5RWDT Ch. 1 - Prob. 6RWDT Ch. 1 - Prob. 7RWDT Ch. 1 - Prob. 8RWDT Ch. 1 - Prob. 9RWDT Ch. 1 - Prob. 10RWDT Ch. 1 - Prob. 1RE Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Prob. 9RE Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 21RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - Prob. 27RE Ch. 1 - Prob. 28RE Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - Prob. 35RE Ch. 1 - Prob. 36RE Ch. 1 - Prob. 37RE Ch. 1 - Prob. 38RE Ch. 1 - Prob. 39RE Ch. 1 - Prob. 40RE Ch. 1 - Prob. 41RE Ch. 1 - Prob. 42RE Ch. 1 - Prob. 43RE Ch. 1 - Prob. 44RE Ch. 1 - Prob. 45RE Ch. 1 - Prob. 46RE Ch. 1 - Prob. 47RE Ch. 1 - Prob. 48RE Ch. 1 - Prob. 49RE Ch. 1 - Prob. 50RE Ch. 1 - Prob. 51RE Ch. 1 - Prob. 52RE Ch. 1 - Prob. 53RE Ch. 1 - Prob. 54RE Ch. 1 - Prob. 55EP Ch. 1 - Prob. 56EP Ch. 1 - Prob. 57EP

Knowledge Booster

Background pattern image

Similar questions

SEE MORE QUESTIONS

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning

Text book image

Calculus: Early Transcendentals

Calculus

ISBN:9781285741550

Author:James Stewart

Publisher:Cengage Learning

Text book image

Thomas' Calculus (14th Edition)

Calculus

ISBN:9780134438986

Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir

Publisher:PEARSON

Text book image

Calculus: Early Transcendentals (3rd Edition)

Calculus

ISBN:9780134763644

Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz

Publisher:PEARSON

Text book image

Calculus: Early Transcendentals

Calculus

ISBN:9781319050740

Author:Jon Rogawski, Colin Adams, Robert Franzosa

Publisher:W. H. Freeman

Text book image

Calculus

ISBN:9780135189405

Author:Michael Sullivan

Publisher:PEARSON

Text book image

Calculus: Early Transcendental Functions

Calculus

ISBN:9781337552516

Author:Ron Larson, Bruce H. Edwards

Publisher:Cengage Learning

SEE MORE TEXTBOOKS