
(a)
To find: The limit
(a)
Answer to Problem 26RE
The limit is 1.5
Explanation of Solution
Given information: The limit is
Calculation:
The given limit is
The graph shows that the value of
Therefore the required limit is
(b)
To find: The value of
(b)
Answer to Problem 26RE
The value is
Explanation of Solution
Given information: The limit is
Calculation:
The given limit is
See from the graph that when the right side of
Therefore the required limit is
(c)
To find: The value of
(c)
Answer to Problem 26RE
The value is
Explanation of Solution
Given information: The function is
Calculation:
The given function is
From the graph that
Therefore the required value is
(d)
To find: determine the value of
(d)
Answer to Problem 26RE
Explanation of Solution
Given information: From part a)
And part b)
Calculation:
Examine the graph and observe the jump discontinuity at
Therefore, by definition
(e)
To find: The points of discontinuity of.
(e)
Answer to Problem 26RE
Explanation of Solution
Given information: From part d)
Calculation:
Therefore, the points of discontinuity of.
(f)
To find: The removal points on discontinuity.
(f)
Answer to Problem 26RE
There are no removable points of discontinuity.
Explanation of Solution
Given information: The graph is:
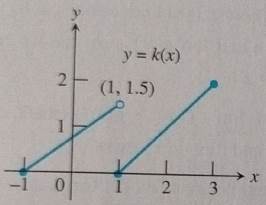
Calculation:
The left and right sides must be equal for the point of discontinuity to be removed. However, at
Therefore, there are no removable points of discontinuity.
Chapter 1 Solutions
CALCULUS-W/XL ACCESS
- EXAMPLE 3 Find S X √√2-2x2 dx. SOLUTION Let u = 2 - 2x². Then du = Χ dx = 2- 2x² = 信 du dx, so x dx = du and u-1/2 du (2√u) + C + C (in terms of x).arrow_forwardLet g(z) = z-i z+i' (a) Evaluate g(i) and g(1). (b) Evaluate the limits lim g(z), and lim g(z). 2-12 (c) Find the image of the real axis under g. (d) Find the image of the upper half plane {z: Iz > 0} under the function g.arrow_forwardk (i) Evaluate k=7 k=0 [Hint: geometric series + De Moivre] (ii) Find an upper bound for the expression 1 +2x+2 where z lies on the circle || z|| = R with R > 10. [Hint: Use Cauchy-Schwarz]arrow_forward
- Hint: You may use the following derivative rules: ddxsin(x)=cos(x) ddxcos(x)=−sin(x) ddxln(x)=1x Find the equation of the tangent line to the curve y=4sinx at the point (π6,2).The equation of this tangent line isarrow_forwardQuestion Find the following limit. Select the correct answer below: 1 2 0 4 5x lim sin (2x)+tan 2 x→arrow_forward12. [0/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.022. Evaluate the indefinite integral. (Use C for the constant of integration.) sin(In 33x) dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





