Chapter 1.1, Problem 59PS

Solution

a.

To write: The verbal model and a quadratic function that represents the weekly profit of the theater.

Verbal model: $\begin{array}{ccccccc}\begin{array}{l}\text{Profit}\\ \left(\text{dollars}\right)\end{array}& =& \begin{array}{l}\text{Price}\\ \text{(dollar/ticket)}\end{array}& \times & \begin{array}{l}\text{Sales}\\ \left(\text{tickets}\right)\end{array}& -& \begin{array}{l}\text{Cost}\\ \left(\text{dollars}\right)\end{array}\end{array}$

Quadratic model: $P\left(x\right)=-10x^2+50x+1500$

Given information:

The theater sells 150 tickets to a play weekly when the price is $20, and for each $1 decrease in the price, the sale increases by 10 tickets per week.

Concept used:

Profit = Revenue − cost

Calculation:

Since the profit revenue minus total cost, the verbal model for the theater’s profit can be given as:

  $\begin{array}{ccccccc}\begin{array}{l}\text{Profit}\\ \left(\text{dollars}\right)\end{array}& =& \begin{array}{l}\text{Price}\\ \text{(dollar/ticket)}\end{array}& \times & \begin{array}{l}\text{Sales}\\ \left(\text{tickets}\right)\end{array}& -& \begin{array}{l}\text{Cost}\\ \left(\text{dollars}\right)\end{array}\end{array}$

Let the price be decreased $x$ times.

So, the price of the ticket becomes $\$\left(20-x\right)$ , and the number of tickets sold becomes $150+10x$ .

Then, the revenue will be $R\left(x\right)=\left(20-x\right)\left(150+10x\right)$ .

Therefore, the function modelling the situation can be written as follows: $\begin{array}{c}P\left(x\right)=\left(20-x\right)\left(150+10x\right)-1500\\ =3000+50x-10x^2-1500\\ =-10x^2+50x+3000-1500\\ =-10x^2+50x+1500\end{array}$ .

b.

To make: A table of values for the quadratic function.

  $\begin{array}{cc}x& P\left(x\right)\\ 1& 1540\\ 2& 1560\\ 3& 1560\\ 4& 1540\end{array}$

Given information:

The theater sells 150 tickets to a play weekly when the price is $20, and for each $1 decrease in the price, the sale increases by 10 tickets per week.

Concept used:

Take a random value of x and substitute in the function to find the value of y, and then use the pair of points to make the table.

Calculation:

The quadratic function for the situation is $P\left(x\right)=-10x^2+50x+1500$ .

When $x=1$ ;

  $\begin{array}{c}P\left(1\right)=-10\cdot 1^2+50\cdot 1+1500\\ =\text{1540}\end{array}$

When $x=2$ ,

  $\begin{array}{c}P\left(2\right)=-10\cdot 2^2+50\cdot 2+1500\\ =\text{1560}\end{array}$

When $x=3$ ,

  $\begin{array}{c}P\left(3\right)=-10\cdot 3^2+50\cdot 3+1500\\ =\text{1560}\end{array}$

When $x=4$ ,

  $\begin{array}{c}P\left(3\right)=-10\cdot 4^2+50\cdot 4+1500\\ =\text{1540}\end{array}$

Now, construct the table based on these values.

  $\begin{array}{cc}x& P\left(x\right)\\ 1& 1540\\ 2& 1560\\ 3& 1560\\ 4& 1540\end{array}$

c.

To graph and find: The graph of the quadratic function using the table and then find how the theater can maximize the profit.

  

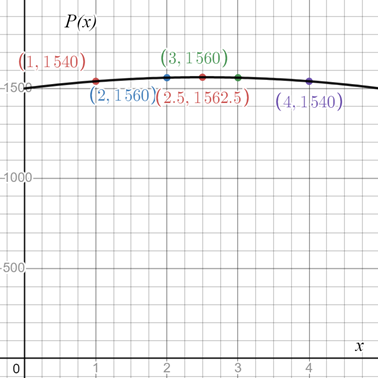
The theater can maximize the profit offering each ticket for $\$17.5$ .

Given information:

The theater sells 150 tickets to a play weekly when the price is $20, and for each $1 decrease in the price, the sale increases by 10 tickets per week.

Concept used:

The vertex of the quadratic function represents the maximum/minimum point of the function.

Calculation:

Plot the points found in part (b) and join them with a smooth curve as follows:

  

Observe that the vertex of the quadratic function is at the point $\left(2.5,1562.5\right)$ . That means, the maximum value of the function is attained when $x=2.5$ .

When $x=2.5$ , the price of each ticket becomes $\$\left(20-2.5\right)=\$17.5$ .

Therefore, the theater can maximize the profit offering each ticket for $\$17.5$ .

Conclusion:

The theater can maximize the profit offering each ticket for $\$17.5$ .