
a.
Check whether there is evidence that there is a difference in the mean selling price of homes with a pool and without a pool.
a.
Answer to Problem 47DA
The conclusion is that there is no evidence of a difference in the mean selling prices of homes with a pool and without a pool.
Explanation of Solution
Calculation:
In this context, let
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Significance level,
It is given that the significance level,
Degrees of freedom:
The degrees of freedom is as follows:
Step-by-step procedure to obtain the critical values using MINITAB software:
- Choose Graph > Probability Distribution Plot choose View Probability > OK.
- From Distribution, choose ‘t’ distribution.
- In Degrees of freedom, enter 103.
- Click the Shaded Area tab.
- Choose Probability and Both Tails for the region of the curve to shade.
- Enter the Probability as 0.05.
- Click OK.
Output obtained using MINITAB software is given below:
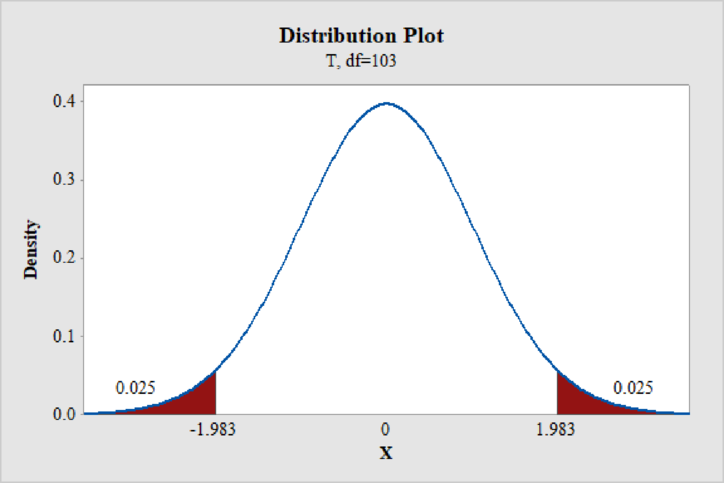
From the MINITAB output, the critical values are
The decision rule is as follows:
If
If
If
Test statistic:
Software procedure:
Step-by-step procedure to obtain the P-value and test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 2 sample t.
- Choose Samples in different columns.
- In Sample 1, enter the column of Without pool.
- In Sample 2, enter the column of With pool.
- Choose Assume equal variance.
- Choose Options.
- In Confidence level, enter 95.
- In Alternative, select not equal.
- Click OK in all the dialogue boxes.
Output obtained using MINITAB software is given below:
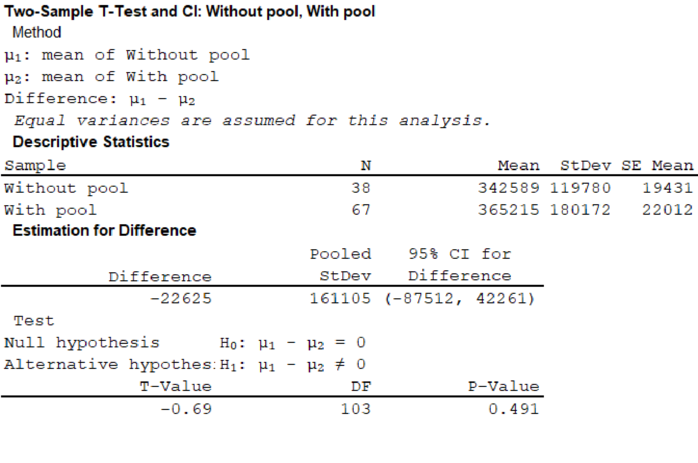
From the given MINITAB output, the value of the test statistic is –0.69.
Decision:
The critical values are ±1.983.
The value of test statistic is –0.69.
The value of test statistic lies between the critical values.
That is,
From the decision rule, fail to reject the null hypothesis.
Therefore, there is no evidence of a difference in the mean selling prices of homes with a pool and without a pool.
b.
Check whether there is evidence of a difference in the mean selling prices of homes with an attached garage and without an attached garage.
b.
Answer to Problem 47DA
The conclusion is that there is evidence of difference in the mean selling prices of homes with an attached garage and homes without an attached garage.
Explanation of Solution
Calculation:
In this context,
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Significance level,
It is given that the significance level,
Degrees of freedom:
The degrees of freedom is as follows:
From the Part a, the critical values are
Test statistic:
Software procedure:
Step-by-step procedure to obtain the P-value and test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 2 sample t.
- Choose Samples in different columns.
- In Sample 1, enter the column of Without garage.
- In Sample 2, enter the column of With garage.
- Choose Assume equal variance.
- Choose Options.
- In Confidence level, enter 95.
- In Alternative, select not equal.
- Click OK in all the dialogue boxes.
Output obtained using MINITAB software is given below:

From the given MINITAB output, the value of the test statistic is –4.28.
Decision:
The critical values are ±1.983.
The value of test statistic is –4.28.
The value of test statistic is less than the critical value –1.983.
That is,
From the decision rule, reject the null hypothesis.
Therefore, there is evidence of difference in the mean selling prices of homes with an attached garage and without an attached garage.
c.
Check whether there is evidence of a difference in the mean selling price of homes that are in default on the mortgage and not in default on the mortgage.
c.
Answer to Problem 47DA
The conclusion is that there is no evidence of difference in the mean selling prices of homes that are in default on the mortgage and not in default on the mortgage.
Explanation of Solution
Calculation:
In this context,
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Significance level,
It is given that the significance level,
Degrees of freedom:
The degrees of freedom is as follows:
From Part a, the critical values are
Test statistic:
Software procedure:
Step-by-step procedure to obtain the P-value and test statistic using MINITAB software:
- Choose Stat > Basic Statistics > 2 sample t.
- Choose Samples in different columns.
- In Sample 1, enter the column of not default.
- In Sample 2, enter the column of default.
- Choose Assume equal variance.
- Choose Options.
- In Confidence level, enter 95.
- In Alternative, select not equal.
- Click OK in all the dialogue boxes.
Output obtained using MINITAB software is given below:

From the given MINITAB output, the value of the test statistic is 0.39.
Decision:
The critical values are ±1.983.
The value of test statistic is 0.39.
The value of test statistic lies between the critical values.
That is,
From the decision rule, fail to reject the null hypothesis.
Therefore, there is no evidence that the difference in the mean selling price of homes that is in default on the mortgage and homes not default on the mortgage.
Want to see more full solutions like this?
Chapter 11 Solutions
Loose Leaf for Statistical Techniques in Business and Economics
- please find the answers for the yellows boxes using the information and the picture belowarrow_forwardA marketing agency wants to determine whether different advertising platforms generate significantly different levels of customer engagement. The agency measures the average number of daily clicks on ads for three platforms: Social Media, Search Engines, and Email Campaigns. The agency collects data on daily clicks for each platform over a 10-day period and wants to test whether there is a statistically significant difference in the mean number of daily clicks among these platforms. Conduct ANOVA test. You can provide your answer by inserting a text box and the answer must include: also please provide a step by on getting the answers in excel Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value.arrow_forwardA company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forward
- Business Discussarrow_forwardThe following data represent total ventilation measured in liters of air per minute per square meter of body area for two independent (and randomly chosen) samples. Analyze these data using the appropriate non-parametric hypothesis testarrow_forwardeach column represents before & after measurements on the same individual. Analyze with the appropriate non-parametric hypothesis test for a paired design.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


