
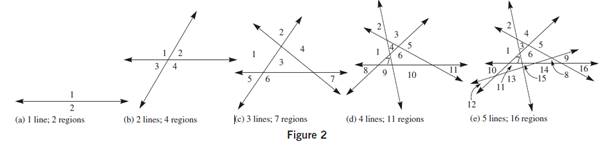
Just as a point separates a line into three parts, a line separates a plane into three parts: the line and two half-planes as shown in Table 4. Two lines can separate a plane into a maximum of 4 parts, and so on. Figure 2 shows the first few cases. Conjecture an expression for the maximum number of regions into which n lines in a plane separate the plane, if the lines themselves are not included.
To find:
The expression for the maximum numbers of regions for 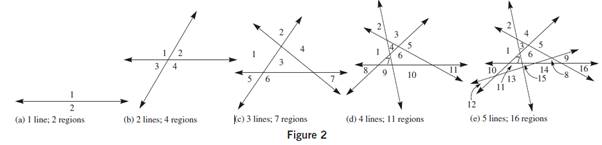
Answer to Problem 2NT
Solution:
Explanation of Solution
Formula used:
The sum of first n numbers is
Calculation:
Given that, the one line can separate a plane into a maximum of 2 parts. The two lines can separate a plane into a maximum of 4 parts, three lines can separate a plane into a maximum of 7 parts, four lines can separate a plane into a maximum of 11 parts, and five lines can separate a plane into a maximum of 16 parts and so on.
If
Computethe equations by using the figure.
Add all the above equation as follows.
Solve the equation as follws.
Therefore, the expression for the maximum numbers of regions for
Want to see more full solutions like this?
Chapter 11 Solutions
A Problem Solving Approach to Mathematics for Elementary School Teachers, Books a la Carte Edition plus NEW MyLab Math with Pearson eText - Access Card Package (12th Edition)
- How many quadrillion BTU were generated using renewable energy sources?arrow_forwardThe final answer is 8/π(sinx) + 8/3π(sin 3x)+ 8/5π(sin5x)....arrow_forwardKeity x२ 1. (i) Identify which of the following subsets of R2 are open and which are not. (a) A = (2,4) x (1, 2), (b) B = (2,4) x {1,2}, (c) C = (2,4) x R. Provide a sketch and a brief explanation to each of your answers. [6 Marks] (ii) Give an example of a bounded set in R2 which is not open. [2 Marks] (iii) Give an example of an open set in R2 which is not bounded. [2 Marksarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

