EBK MATHEMATICS FOR THE TRADES
11th Edition
ISBN: 8220106960455
Author: CARMAN
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 1.1, Problem 2EE
E. Calculator Problems
You probably own a calculator and, of course, you are eager to put it to work doing practical math calculations. In this text we include problem sets for calculator users. These problems are taken from real-life situations and, unlike most textbook problems, involve big numbers and lots of calculations. If you think that having an electronic brain-in-a-box means that you do not need to know basic arithmetic, you will be disappointed. The calculator helps you to work faster, but it will not tell you what to do or how to do it.
Detailed instructions on using a calculator with whole numbers appears on page 68.
Here are a few helpful hints for calculator users:
- 1. Always estimate your answer before doing a calculation.
- 2. Check your answer by comparing it with the estimate or by the other methods shown in this text. Be certain that your answer makes sense.
- 3. If you doubt the calculator (they do break down, you know), put a problem in it whose answer you know, preferably a problem like the one you are solving.
Manufacturing The following table lists the number of widget fasteners made by each of the five machines at the Ace Widget Co. during the last ten working days.
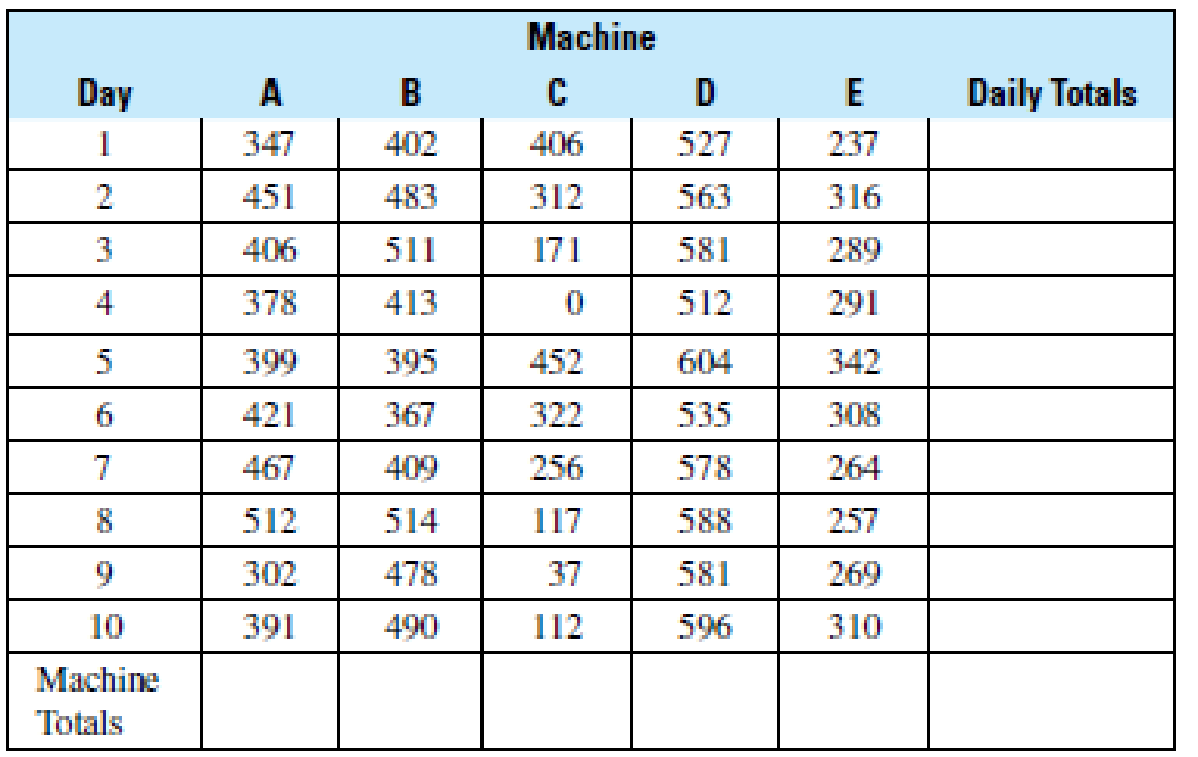
- (a) Complete the table by finding the number of fasteners produced each day. Enter these totals under the column “Daily Totals” on the right.
- (b) Find the number of fasteners produced by each machine during the ten-day period and enter these totals along the bottom row marked “Machine Totals.”
- (c) Does the sum of the daily totals equal the sum of the machine totals?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online.
A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions:
Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means.
Using the results from Question 1, make recommendation for…
Question 9
1
5
4
3
2
1
-8 -7 -05 -4 -3 -2 1
1 2
3 4 5 6 7 8
-1
7
-2
-3
-4
-5+
1-6+
For the graph above, find the function of the form -tan(bx) + c
f(x) =
Question 8
5
4
3
2
1
-8 -7 -6 -5/-4 -3 -2 -1,
1 2 3 4 5 6 7/8
-1
-2
-3
-4
-5
0/1 pt 3 98 C
-6
For the graph above, find the function of the form f(x)=a tan(bx) where a=-1 or +1 only
f(x) =
=
Question Help: Video
Submit Question Jump to Answer
Chapter 1 Solutions
EBK MATHEMATICS FOR THE TRADES
Ch. 1.1 - Write in numerical form: two hundred six thousand,...Ch. 1.1 - Round the number in problem 1 to the nearest...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...
Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Write as numbers. Three thousand, sixCh. 1.1 - Write as numbers. Seventeen thousand, twenty-fourCh. 1.1 - Write as numbers. Eleven thousand, one hundredCh. 1.1 - Write as numbers. Three million, two thousand,...Ch. 1.1 - Write as numbers. Four million, forty thousand,...Ch. 1.1 - Prob. 16AECh. 1.1 - Round as indicated. 357 to the nearest tenCh. 1.1 - Round as indicated. 4386 to the nearest hundredCh. 1.1 - Round as indicated. 4386 to the nearest thousandCh. 1.1 - Round as indicated. 15,472 to the nearest thousandCh. 1.1 - Round as indicated. 225,799 to the nearest ten...Ch. 1.1 - Round as indicated. 32,408,792 to the nearest...Ch. 1.1 - Add. 4722_Ch. 1.1 - Add. 2731_Ch. 1.1 - Add. 4535_Ch. 1.1 - Add. 3855_Ch. 1.1 - Add. 7548_Ch. 1.1 - Add. 2698_Ch. 1.1 - Add. 4884_Ch. 1.1 - Add. 6769_Ch. 1.1 - Add. 74759_Ch. 1.1 - Add. 50895_Ch. 1.1 - Prob. 11BECh. 1.1 - Add. 432399_Ch. 1.1 - Add. 621388_Ch. 1.1 - Add. 189204_Ch. 1.1 - Add. 375486_Ch. 1.1 - Add. 4237288_Ch. 1.1 - Prob. 17BECh. 1.1 - Prob. 18BECh. 1.1 - Add. 37857643_Ch. 1.1 - Prob. 20BECh. 1.1 - Add. 10674397_Ch. 1.1 - Add. 400267085_Ch. 1.1 - Prob. 23BECh. 1.1 - Add. 198764835_Ch. 1.1 - Add. 7804497684_Ch. 1.1 - Prob. 26BECh. 1.1 - Add. 581824433_Ch. 1.1 - Prob. 28BECh. 1.1 - Prob. 29BECh. 1.1 - B. Add.Ch. 1.1 - C. Arrange vertically and find the sum. 487 + 29 +...Ch. 1.1 - Prob. 2CECh. 1.1 - C. Arrange vertically and find the sum. 322 + 46 +...Ch. 1.1 - C. Arrange vertically and find the sum. 7268 + 209...Ch. 1.1 - Prob. 5CECh. 1.1 - C. Arrange vertically and find the sum. 715 + 4293...Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 11CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 13CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 15CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 19CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - D. Practical Applications. Electrical Trades In...Ch. 1.1 - D. Practical Applications. Flooring and Carpeting...Ch. 1.1 - D. Practical Applications. Machine Trades The...Ch. 1.1 - D. Practical Applications. Trades Management In...Ch. 1.1 - D. Practical Applications. Trades Management The...Ch. 1.1 - D. Practical Applications. Roofing On a home...Ch. 1.1 - Prob. 7DECh. 1.1 - D. Practical Applications. Automotive Trades A...Ch. 1.1 - D. Practical Applications. Construction The Happy...Ch. 1.1 - D. Practical Applications. Machine Trades A...Ch. 1.1 - D. Practical Applications. Landscaping A new...Ch. 1.1 - Prob. 12DECh. 1.1 - D. Practical Applications. Electronics When...Ch. 1.1 - Prob. 14DECh. 1.1 - Prob. 15DECh. 1.1 - D. Practical Applications. Allied Health The...Ch. 1.1 - D. Practical Applications. Construction For...Ch. 1.1 - D. Practical Applications. Automotive Trades The...Ch. 1.1 - D. Practical Applications. Sports and Leisure In...Ch. 1.1 - Prob. 1EECh. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.2 - Do the following without using a calculator: Add:...Ch. 1.2 - Do the following without using a calculator:...Ch. 1.2 - Subtract. 427_Ch. 1.2 - Prob. 2AECh. 1.2 - Subtract. 349_Ch. 1.2 - Prob. 4AECh. 1.2 - Prob. 5AECh. 1.2 - Prob. 6AECh. 1.2 - Prob. 7AECh. 1.2 - Subtract. 9622_Ch. 1.2 - Prob. 9AECh. 1.2 - Prob. 10AECh. 1.2 - Prob. 11AECh. 1.2 - Subtract. 3617_Ch. 1.2 - Prob. 13AECh. 1.2 - Subtract. 5216_Ch. 1.2 - Subtract. 6527_Ch. 1.2 - Prob. 16AECh. 1.2 - Prob. 17AECh. 1.2 - Subtract. 7048_Ch. 1.2 - Subtract. 349_Ch. 1.2 - Prob. 20AECh. 1.2 - Subtract. 546357_Ch. 1.2 - Prob. 22AECh. 1.2 - Prob. 23AECh. 1.2 - Prob. 24AECh. 1.2 - Prob. 25AECh. 1.2 - Prob. 26AECh. 1.2 - Prob. 27AECh. 1.2 - Prob. 28AECh. 1.2 - Prob. 29AECh. 1.2 - Prob. 30AECh. 1.2 - Prob. 31AECh. 1.2 - Prob. 32AECh. 1.2 - Prob. 33AECh. 1.2 - Prob. 34AECh. 1.2 - Subtract. 5007266_Ch. 1.2 - Prob. 36AECh. 1.2 - Prob. 37AECh. 1.2 - Prob. 38AECh. 1.2 - Prob. 1BECh. 1.2 - Prob. 2BECh. 1.2 - Prob. 3BECh. 1.2 - Prob. 4BECh. 1.2 - Prob. 5BECh. 1.2 - Prob. 6BECh. 1.2 - Prob. 7BECh. 1.2 - Prob. 8BECh. 1.2 - B. Practical Applications Automotive Trades A...Ch. 1.2 - B. Practical Applications Construction A truck...Ch. 1.2 - Prob. 11BECh. 1.2 - Prob. 12BECh. 1.2 - Prob. 13BECh. 1.2 - Prob. 14BECh. 1.2 - B Practical Applications Electronics An electronic...Ch. 1.2 - B Practical Applications Automotive Trades A set...Ch. 1.2 - Prob. 17BECh. 1.2 - B Practical Applications General Interest The...Ch. 1.2 - B Practical Applications Life Skills A potential...Ch. 1.2 - C. Calculator Problems Plumbing The Karroll...Ch. 1.2 - C. Calculator Problems Which sum is greater?Ch. 1.2 - C. Calculator Problems Trades Management If an...Ch. 1.2 - C. Calculator Problems Trades Management The...Ch. 1.2 - C. Calculator Problems Life Skills Balance the...Ch. 1.2 - C. Calculator Problems Construction A water meter...Ch. 1.3 - Subtract: 572286Ch. 1.3 - Multiply: 69Ch. 1.3 - Prob. 1AECh. 1.3 - Multiply. 78_Ch. 1.3 - Prob. 3AECh. 1.3 - Prob. 4AECh. 1.3 - Prob. 5AECh. 1.3 - Prob. 6AECh. 1.3 - Prob. 7AECh. 1.3 - Prob. 8AECh. 1.3 - Prob. 9AECh. 1.3 - Prob. 10AECh. 1.3 - Prob. 11AECh. 1.3 - Prob. 12AECh. 1.3 - Prob. 13AECh. 1.3 - Prob. 14AECh. 1.3 - Prob. 15AECh. 1.3 - Prob. 16AECh. 1.3 - Prob. 17AECh. 1.3 - Prob. 18AECh. 1.3 - Prob. 19AECh. 1.3 - Prob. 20AECh. 1.3 - Prob. 21AECh. 1.3 - Prob. 22AECh. 1.3 - Multiply. 7211_Ch. 1.3 - Prob. 24AECh. 1.3 - Prob. 25AECh. 1.3 - Prob. 26AECh. 1.3 - Prob. 27AECh. 1.3 - Prob. 28AECh. 1.3 - Prob. 29AECh. 1.3 - Prob. 30AECh. 1.3 - Prob. 31AECh. 1.3 - Multiply. 6625_Ch. 1.3 - Prob. 33AECh. 1.3 - Prob. 34AECh. 1.3 - Prob. 35AECh. 1.3 - Prob. 36AECh. 1.3 - Prob. 1BECh. 1.3 - Multiply. 6097_Ch. 1.3 - Prob. 3BECh. 1.3 - Prob. 4BECh. 1.3 - Prob. 5BECh. 1.3 - Prob. 6BECh. 1.3 - Prob. 7BECh. 1.3 - Prob. 8BECh. 1.3 - Prob. 9BECh. 1.3 - Prob. 10BECh. 1.3 - Prob. 11BECh. 1.3 - Prob. 12BECh. 1.3 - Prob. 13BECh. 1.3 - Multiply. 542600_Ch. 1.3 - Multiply. 7009504_Ch. 1.3 - Prob. 16BECh. 1.3 - Prob. 17BECh. 1.3 - Prob. 18BECh. 1.3 - Prob. 19BECh. 1.3 - Prob. 20BECh. 1.3 - Prob. 1CECh. 1.3 - Prob. 2CECh. 1.3 - Prob. 3CECh. 1.3 - Prob. 4CECh. 1.3 - Prob. 5CECh. 1.3 - Prob. 6CECh. 1.3 - Prob. 7CECh. 1.3 - Practical Applications Construction What is the...Ch. 1.3 - Prob. 9CECh. 1.3 - Prob. 10CECh. 1.3 - Prob. 11CECh. 1.3 - Prob. 12CECh. 1.3 - Practical Applications Machine Trades If a machine...Ch. 1.3 - C. Practical Applications Electronics For a...Ch. 1.3 - C. Practical Applications Roofing In the Happy...Ch. 1.3 - C. Practical Applications Electronics A 78-ohm...Ch. 1.3 - Prob. 17CECh. 1.3 - Prob. 18CECh. 1.3 - Prob. 19CECh. 1.3 - Prob. 20CECh. 1.3 - Prob. 21CECh. 1.3 - Prob. 22CECh. 1.3 - Prob. 23CECh. 1.3 - Prob. 24CECh. 1.3 - Prob. 25CECh. 1.3 - Prob. 26CECh. 1.3 - Water/Wastewater Treatment A rural water district...Ch. 1.3 - Prob. 28CECh. 1.3 - Prob. 29CECh. 1.3 - Calculator Problems Business and Finance If an...Ch. 1.3 - Prob. 2DECh. 1.3 - Prob. 3DECh. 1.3 - Prob. 4DECh. 1.3 - Prob. 5DECh. 1.3 - Prob. 6DECh. 1.4 - Multiply: 3845Ch. 1.4 - Prob. 2LCCh. 1.4 - A. Divide. 63 7Ch. 1.4 - Prob. 2AECh. 1.4 - Prob. 3AECh. 1.4 - Prob. 4AECh. 1.4 - A. Divide. 54 9Ch. 1.4 - Prob. 6AECh. 1.4 - A. Divide. 725Ch. 1.4 - Prob. 8AECh. 1.4 - Prob. 9AECh. 1.4 - Prob. 10AECh. 1.4 - Prob. 11AECh. 1.4 - Prob. 12AECh. 1.4 - Prob. 13AECh. 1.4 - Prob. 14AECh. 1.4 - A. Divide. 14767Ch. 1.4 - A. Divide. 7364Ch. 1.4 - Prob. 17AECh. 1.4 - A. Divide. 42018Ch. 1.4 - A. Divide. 92000Ch. 1.4 - A. Divide. 71000Ch. 1.4 - A. Divide. 73507Ch. 1.4 - Prob. 22AECh. 1.4 - Prob. 23AECh. 1.4 - Prob. 24AECh. 1.4 - Divide. 322 14Ch. 1.4 - Prob. 2BECh. 1.4 - Prob. 3BECh. 1.4 - Prob. 4BECh. 1.4 - Prob. 5BECh. 1.4 - Prob. 6BECh. 1.4 - Prob. 7BECh. 1.4 - Prob. 8BECh. 1.4 - B. Divide. 42371Ch. 1.4 - Prob. 10BECh. 1.4 - Prob. 11BECh. 1.4 - Prob. 12BECh. 1.4 - Prob. 13BECh. 1.4 - B. Divide. 2400 75Ch. 1.4 - Prob. 15BECh. 1.4 - Prob. 16BECh. 1.4 - Prob. 17BECh. 1.4 - Prob. 18BECh. 1.4 - Prob. 19BECh. 1.4 - B. Divide. 4794425Ch. 1.4 - Prob. 21BECh. 1.4 - B. Divide. 23114091Ch. 1.4 - Prob. 23BECh. 1.4 - Prob. 24BECh. 1.4 - Prob. 25BECh. 1.4 - Prob. 26BECh. 1.4 - Prob. 27BECh. 1.4 - Prob. 28BECh. 1.4 - Prob. 29BECh. 1.4 - C. For each of the following whole numbers, (a)...Ch. 1.4 - Prob. 2CECh. 1.4 - Prob. 3CECh. 1.4 - Prob. 4CECh. 1.4 - Prob. 5CECh. 1.4 - C. For each of the following whole numbers, (a)...Ch. 1.4 - D. Applied Problems Machine Trades A machinist has...Ch. 1.4 - Prob. 2DECh. 1.4 - Prob. 3DECh. 1.4 - Prob. 4DECh. 1.4 - Prob. 5DECh. 1.4 - Prob. 6DECh. 1.4 - Prob. 7DECh. 1.4 - Prob. 8DECh. 1.4 - Prob. 9DECh. 1.4 - D. Applied Problems Transportation A delivery...Ch. 1.4 - D. Applied Problems Automotive Trades A mechanic...Ch. 1.4 - D. Applied Problems Metalworking One cubic foot of...Ch. 1.4 - D. Applied Problems Printing A printer needs...Ch. 1.4 - D. Applied Problems Water/Wastewater Treatment A...Ch. 1.4 - D. Applied Problems HVAC A geothermal heat pump...Ch. 1.4 - Prob. 16DECh. 1.4 - D. Applied Problems HVAC A family wants to replace...Ch. 1.4 - D. Applied Problems Agriculture Barley weighs 48...Ch. 1.4 - D. Applied Problems Water/Wastewater Treatment A...Ch. 1.4 - D. Applied Problems Electrical Trades A...Ch. 1.4 - D. Applied Problems Carpentry Each 8-foot length...Ch. 1.4 - D. Applied Problems Automotive Trades The...Ch. 1.4 - E. Calculator Problems Calculate the following....Ch. 1.4 - Prob. 2EECh. 1.4 - Prob. 3EECh. 1.4 - Prob. 4EECh. 1.4 - Prob. 5EECh. 1.4 - E. Calculator Problems Painting Following are four...Ch. 1.4 - Prob. 7EECh. 1.5 - Divide 24768Ch. 1.5 - Calculate: 8 4 2Ch. 1.5 - Perform all operations in the correct order. 2 + 8...Ch. 1.5 - Prob. 2AECh. 1.5 - Perform all operations in the correct order. 40 ...Ch. 1.5 - Perform all operations in the correct order. 16 +...Ch. 1.5 - Prob. 5AECh. 1.5 - Prob. 6AECh. 1.5 - Prob. 7AECh. 1.5 - Perform all operations in the correct order. 64 ...Ch. 1.5 - Prob. 9AECh. 1.5 - Prob. 10AECh. 1.5 - Prob. 11AECh. 1.5 - Prob. 12AECh. 1.5 - Prob. 13AECh. 1.5 - Prob. 14AECh. 1.5 - Prob. 15AECh. 1.5 - Prob. 16AECh. 1.5 - Prob. 17AECh. 1.5 - Prob. 18AECh. 1.5 - Prob. 19AECh. 1.5 - Prob. 20AECh. 1.5 - Prob. 21AECh. 1.5 - Perform all operations in the correct order. 54 ...Ch. 1.5 - Perform all operations in the correct order. (4 3...Ch. 1.5 - Prob. 24AECh. 1.5 - Prob. 25AECh. 1.5 - Prob. 26AECh. 1.5 - Prob. 27AECh. 1.5 - Prob. 28AECh. 1.5 - Perform all operations in the correct order. 12 7...Ch. 1.5 - Prob. 30AECh. 1.5 - Prob. 31AECh. 1.5 - Prob. 32AECh. 1.5 - Prob. 33AECh. 1.5 - Prob. 34AECh. 1.5 - Prob. 35AECh. 1.5 - Prob. 36AECh. 1.5 - Prob. 37AECh. 1.5 - Prob. 38AECh. 1.5 - Prob. 39AECh. 1.5 - Prob. 40AECh. 1.5 - Painting A painter ordered 3 gallons of acrylic...Ch. 1.5 - Landscaping On a certain landscaping job, Steve...Ch. 1.5 - Prob. 3BECh. 1.5 - Prob. 4BECh. 1.5 - Prob. 5BECh. 1.5 - Prob. 6BECh. 1.5 - Prob. 7BECh. 1.5 - Prob. 8BECh. 1.5 - Prob. 9BECh. 1.5 - Prob. 10BECh. 1.5 - Prob. 11BECh. 1.5 - C. Calculator Problems 462 + 83 95Ch. 1.5 - Prob. 2CECh. 1.5 - Prob. 3CECh. 1.5 - Prob. 4CECh. 1.5 - Prob. 5CECh. 1.5 - Prob. 6CECh. 1.5 - Prob. 7CECh. 1.5 - Prob. 8CECh. 1.5 - Prob. 9CECh. 1.5 - Prob. 10CECh. 1.5 - C. Calculator Problems 864 16 27Ch. 1.5 - Prob. 12CECh. 1.5 - Prob. 13CECh. 1.5 - Prob. 14CECh. 1.5 - Prob. 15CECh. 1.5 - Prob. 16CECh. 1 - (a) Write whole numbers in words. (b) Write, in...Ch. 1 - Round whole numbers. Round 214,659 (a) to the...Ch. 1 - Add whole numbers. (a) 67 + 58 (b) 7009 + 1598Ch. 1 - Prob. 4PCh. 1 - Prob. 5PCh. 1 - Prob. 6PCh. 1 - Prob. 7PCh. 1 - Use the correct order of operations with addition,...Ch. 1 - Prob. 9PCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 3APSCh. 1 - Prob. 4APSCh. 1 - Prob. 5APSCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 7APSCh. 1 - Prob. 8APSCh. 1 - Prob. 9APSCh. 1 - Prob. 10APSCh. 1 - Prob. 11APSCh. 1 - Prob. 12APSCh. 1 - Prob. 13APSCh. 1 - Prob. 14APSCh. 1 - Prob. 15APSCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 18APSCh. 1 - Prob. 19APSCh. 1 - Prob. 20APSCh. 1 - Prob. 21APSCh. 1 - Prob. 1BPSCh. 1 - Prob. 2BPSCh. 1 - Prob. 3BPSCh. 1 - Prob. 4BPSCh. 1 - Prob. 5BPSCh. 1 - Prob. 6BPSCh. 1 - Prob. 7BPSCh. 1 - Prob. 8BPSCh. 1 - Prob. 9BPSCh. 1 - Prob. 10BPSCh. 1 - Prob. 11BPSCh. 1 - Prob. 12BPSCh. 1 - Perform the arithmetic as shown. 734 85Ch. 1 - Prob. 14BPSCh. 1 - Prob. 15BPSCh. 1 - Prob. 16BPSCh. 1 - Perform the arithmetic as shown. 376 4Ch. 1 - Prob. 18BPSCh. 1 - Prob. 19BPSCh. 1 - Prob. 20BPSCh. 1 - B. Perform the arithmetic as shown. 207 63Ch. 1 - B. Perform the arithmetic as shown. 314 926Ch. 1 - Prob. 23BPSCh. 1 - Prob. 24BPSCh. 1 - Prob. 25BPSCh. 1 - Prob. 26BPSCh. 1 - B. Perform the arithmetic as shown. 422394Ch. 1 - Prob. 28BPSCh. 1 - Prob. 29BPSCh. 1 - Prob. 30BPSCh. 1 - Prob. 31BPSCh. 1 - Prob. 32BPSCh. 1 - B. Perform the arithmetic as shown. 36911342Ch. 1 - Prob. 34BPSCh. 1 - Prob. 35BPSCh. 1 - B. Perform the arithmetic as shown. 32 4 + 16 2 ...Ch. 1 - Prob. 37BPSCh. 1 - Prob. 38BPSCh. 1 - Prob. 39BPSCh. 1 - Prob. 40BPSCh. 1 - Prob. 41BPSCh. 1 - Prob. 42BPSCh. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - D. Practical Applications Electrical Trades From a...Ch. 1 - D. Practical Applications Machine Trades A machine...Ch. 1 - D. Practical Applications Construction Find the...Ch. 1 - D. Practical Applications Allied Health A patient...Ch. 1 - D. Practical Applications Electrical Trades...Ch. 1 - D. Practical Applications Flooring and Carpeting...Ch. 1 - D. Practical Applications Construction The weights...Ch. 1 - Prob. 8DPSCh. 1 - Prob. 9DPSCh. 1 - D. Practical Applications Electronics The output...Ch. 1 - Prob. 11DPSCh. 1 - Prob. 12DPSCh. 1 - D. Practical Applications Fire Protection A fire...Ch. 1 - D. Practical Applications Construction A pile of...Ch. 1 - D. Practical Applications Marine Technology If the...Ch. 1 - D. Practical Applications Automotive Trades A rule...Ch. 1 - D. Practical Applications Machine Trades If it...Ch. 1 - Prob. 18DPSCh. 1 - D. Practical Applications Manufacturing A gallon...Ch. 1 - D. Practical Applications Office Services The Ace...Ch. 1 - D. Practical Applications Manufacturing At 8 A.M....Ch. 1 - D. Practical Applications Fire Protection The...Ch. 1 - D. Practical Applications Carpentry A fireplace...Ch. 1 - D. Practical Applications Electronics When...Ch. 1 - D. Practical Applications Trades Management RAD...Ch. 1 - D. Practical Applications Life Skills An...Ch. 1 - D. Practical Applications Office Services Use the...Ch. 1 - D. Practical Applications Life Skills Gorilla glue...Ch. 1 - D. Practical Applications Automotive Trades A 2017...Ch. 1 - D. Practical Applications Landscaping A landscape...Ch. 1 - Prob. 31DPSCh. 1 - D. Practical Applications Construction A...Ch. 1 - Prob. 33DPSCh. 1 - D. Practical Applications Carpentry A set of eight...Ch. 1 - Agriculture A bushel of oats weighs 32 lb. How...Ch. 1 - Prob. 36DPSCh. 1 - D. Practical Applications HVAC In designing a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online. A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions: Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means. Using the results from Question 1, make recommendation for…arrow_forwardQuestion 10 6 5 4 3 2 -π/4 π/4 π/2 -1 -2 -3- -4 -5- -6+ For the graph above, find the function of the form f(x)=a tan(bx)+c where a=-1 or +1 only f(x) = Question Help: Videoarrow_forwardMODELING REAL LIFE Your checking account has a constant balance of $500. Let the function $m$ represent the balance of your savings account after $t$ years. The table shows the total balance of the accounts over time. Year, $t$ Total balance 0 1 2 3 4 5 $2500 $2540 $2580.80 $2622.42 $2664.86 $2708.16 a. Write a function $B$ that represents the total balance after $t$ years. Round values to the nearest hundredth, if necessary. $B\left(t\right)=$ Question 2 b. Find $B\left(8\right)$ . About $ a Question 3 Interpret $B\left(8\right)$ . b represents the total balance checking and saving accounts after 8 years the balance would be 16 / 10000 Word Limit16 words written of 10000 allowed Question 4 c. Compare the savings account to the account, You deposit $9000 in a savings account that earns 3.6% annual interest compounded monthly. A = 11998.70 SINCE 9000 is the principal ( 1+0.036/12)12 times 8 gives me aproxtimately 1997 14 / 10000 Word Limit14 words written of 10000 allowed Skip to…arrow_forward
- Listen MODELING REAL LIFE Your checking account has a constant balance of $500. Let the function m represent the balance of your savings account after t years. The table shows the total balance of the accounts over time. Year, t Total balance 0 $2500 1 $2540 2 $2580.80 3 $2622.42 4 $2664.86 5 $2708.16 a. Write a function B that represents the total balance after t years. Round values to the nearest hundredth, if necessary. B(t) = 500 + 2000(1.02)* b. Find B(8). About $2843.32 Interpret B(8). B I U E T² T₂ c. Compare the savings account to the account, You deposit $9000 in a savings account that earns 3.6% annual interest compounded monthly. B I U E E T² T₂ A = 11998.70 SINCE 9000 is the principal (1+0.036/12)12 times 8 gives me aproxtimately 1997arrow_forward14. Show that if a, b, and c are integers such that (a, b) = 1 and c | (a+b), then (c, a) = (c, b) = 1.arrow_forwardA retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP). What were the average sales for the standard POP display (control group)? What were the sales for the digital display (experimental group)? What is the (mean) difference in sales between the experimental group and control group? List the null hypothesis being tested. Do you reject or retain the null hypothesis based on the results of the independent t-test? Was the difference between the…arrow_forward
- Using fixed point iteration and Newton Raphson methods to solve the following function: f(x) = e−0.5x(4-x)-2. Take xo-2 and n=5.arrow_forwardUse the information to find and compare Δy and dy. (Round your answers to four decimal places.) y = x4 + 7 x = −3 Δx = dx = 0.01 Δy = dy =arrow_forwardWhat were the average sales for the four weeks prior to the experiment? What were the sales during the four weeks when the stores used the digital display? What is the mean difference in sales between the experimental and regular POP time periods? State the null hypothesis being tested by the paired sample t-test. Do you reject or retain the null hypothesis? At a 95% significance level, was the difference significant? Explain why or why not using the results from the paired sample t-test. Should the manager of the retail chain install new digital displays in each store? Justify your answer.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY