
Concept explainers
a.
Write the distance between the point and the line as a function of
a.
Answer to Problem 19PS
Explanation of Solution
Given information:
Consider the line given by the parametric equations
and the point
Write the distance between the point and the line as a function of
Calculation:
Consider the
Distance between a point Q and line in space with direction vector
The coordinates of point Q is
Hence the direction vector of line will be
Hence the coordinates of a general point on the line will be
Therefore the coordinates of point P is
Hence vector
Now cross product of two vectors and is
Distance vector never consist terms of
Therefore
Hence the distance of given point from the line is
b.
Use the graph to find the value of s.
b.
Answer to Problem 19PS
Explanation of Solution
Given information:
Consider the line given by the parametric equations
and the point
Use a graphing utility to graph the function from part (a). Use the graph to find the value of s such that the distance between the point and the line is a minimum.
Calculation:
Consider the vectors in space
Distance between a point Q and line in space with direction vector
Using
Press
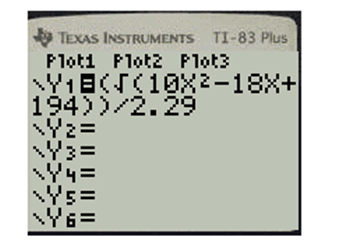
Press
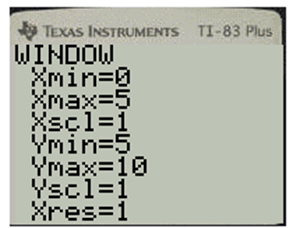
Press
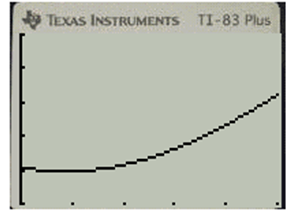
To find the minimum value of function, press “Trace” button and use arrow keys to find the lowest point. Following screen is received.
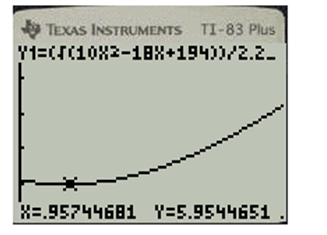
Hence, the minimum distance line and point is
c.
Does it appear that the graph has slant asymptotes?
c.
Answer to Problem 19PS
The function does not have any slant asymptote.
Explanation of Solution
Given information:
Consider the line given by the parametric equations
and the point
Use the zoom feature of the graphing utility to zoom out several times on the graph in part (b). Does it appear that the graph has slant asymptotes? Explain. If it appear to have slant asymptotes, find them.
Calculation:
Consider the vectors in space
Distance between a point Q and line in space with direction vector
Slant asymptote means the range in x-axis where graph have almost infinite slope. In TI-83;
Press “Zoom” button and select “0:ZoomFit”. The following screen appears.
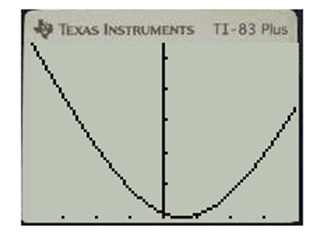
On zooming the graph, there is no such range is found.
Hence the function does not have any slant asymptote.
Chapter 11 Solutions
EBK PRECALCULUS W/LIMITS
- Find the length of the following curve. 3 1 2 N x= 3 -y from y 6 to y=9arrow_forward3 4/3 3213 + 8 for 1 ≤x≤8. Find the length of the curve y=xarrow_forwardGiven that the outward flux of a vector field through the sphere of radius r centered at the origin is 5(1 cos(2r)) sin(r), and D is the value of the divergence of the vector field at the origin, the value of sin (2D) is -0.998 0.616 0.963 0.486 0.835 -0.070 -0.668 -0.129arrow_forward
- 10 The hypotenuse of a right triangle has one end at the origin and one end on the curve y = Express the area of the triangle as a function of x. A(x) =arrow_forwardIn Problems 17-26, solve the initial value problem. 17. dy = (1+ y²) tan x, y(0) = √√3arrow_forwardcould you explain this as well as disproving each wrong optionarrow_forward
- could you please show the computation of this by wiresarrow_forward4 Consider f(x) periodic function with period 2, coinciding with (x) = -x on the interval [,0) and being the null function on the interval [0,7). The Fourier series of f: (A) does not converge in quadratic norm to f(x) on [−π,π] (B) is pointwise convergent to f(x) for every x = R П (C) is in the form - 4 ∞ +Σ ak cos(kx) + bk sin(kx), ak ‡0, bk ‡0 k=1 (D) is in the form ak cos(kx) + bk sin(kx), ak 0, bk 0 k=1arrow_forwardSolve the equation.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





