
Concept explainers
Students are testing their new drone to see if it can safely deliver packages to different departments on campus. Position data can be approximated using the expressions x(t) = −0.0000225t4 + 0.003t3 + 0.01t2 and
(a)
Plot the path of the drone and find the duration (t) of the flight.
Answer to Problem 11.182RP
The duration (t) of the flight is
Explanation of Solution
Given information:
The x coordinate is defined by the relation as
The y coordinate is defined by the relation as
Calculation:
The x coordinate is defined by the relation:
The y coordinate is defined by the relation:
Calculate the duration (t) of the flight:
Equate equation (2) to zero.
General solution for
Calculate the x coordinated as time (t) 0 sec.
Substitute 0 for t in Equation (1).
Similarly calculate the x coordinate for time interval of
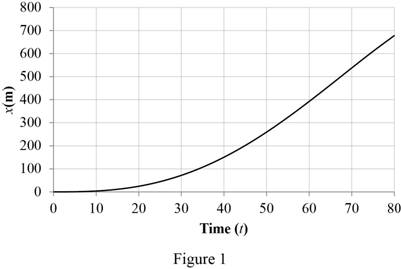
Tabulate the calculated values of x coordinate for time interval
| Time (t)(sec) | x(m) |
| 0 | 0.00 |
| 5 | 0.61 |
| 10 | 3.78 |
| 15 | 11.24 |
| 20 | 24.40 |
| 25 | 44.34 |
| 30 | 71.78 |
| 35 | 107.11 |
| 40 | 150.40 |
| 45 | 201.36 |
| 50 | 259.38 |
| 55 | 323.49 |
| 60 | 392.40 |
| 65 | 464.49 |
| 70 | 537.78 |
| 75 | 609.96 |
| 80 | 678.40 |
Plot the graph for time (t) and x coordinate as in Figure (1).
Calculate the y coordinated as time (t) 0 sec.
Substitute 0 for t in equation (1).
Similarly calculate the y coordinate for time interval of
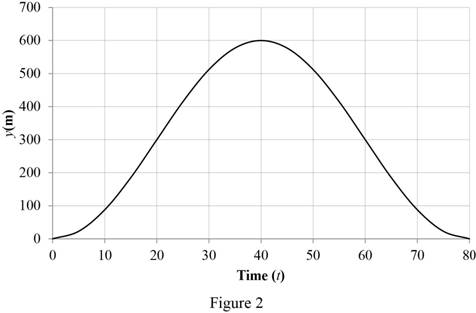
Tabulate the calculated values of y coordinate for time interval
| Time (t)(sec) | y(m) |
| 0 | 0.00 |
| 5 | 22.84 |
| 10 | 87.87 |
| 15 | 185.19 |
| 20 | 300.00 |
| 25 | 414.81 |
| 30 | 512.13 |
| 35 | 577.16 |
| 40 | 600.00 |
| 45 | 577.16 |
| 50 | 512.13 |
| 55 | 414.81 |
| 60 | 300.00 |
| 65 | 185.19 |
| 70 | 87.87 |
| 75 | 22.84 |
| 80 | 0.00 |
Plot the graph for time (t) and y coordinate as in Figure (2).
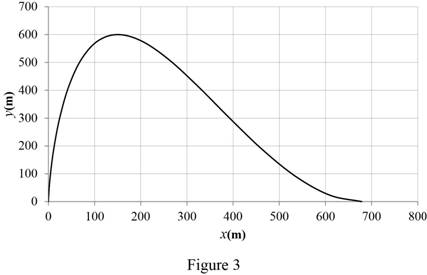
Tabulate the x and y coordinates value as in Table (3):
| x(m) | y(m) |
| 0.00 | 0.00 |
| 0.61 | 22.84 |
| 3.78 | 87.87 |
| 11.24 | 185.19 |
| 24.40 | 300.00 |
| 44.34 | 414.81 |
| 71.78 | 512.13 |
| 107.11 | 577.16 |
| 150.40 | 600.00 |
| 201.36 | 577.16 |
| 259.38 | 512.13 |
| 323.49 | 414.81 |
| 392.40 | 300.00 |
| 464.49 | 185.19 |
| 537.78 | 87.87 |
| 609.96 | 22.84 |
| 678.40 | 0.00 |
Plot the graph for coordinate x and y as in Figure (3).
Therefore, the duration (t) of the flight is
(b)
The maximum speed
Answer to Problem 11.182RP
The maximum speed
Explanation of Solution
Given information:
The x coordinate is defined by the relation as
The y coordinate is defined by the relation as
Calculation:
Differentiate equation (1) with respective to time (t).
Since, the rate of change of any coordinate with respect to time is equal to the velocity.
Differentiate equation (3) with respective to time (t).
Since, the rate of change of velocity with respect to time is equal to the acceleration.
Calculate the time (t) at which the velocity is maximum:
Equate the equation (4) to zero,
Solve the above quadratic equation for the roots (t),
The roots are -1.093 sec and 67.76 sec. Reject the negative root.
Calculate the maximum speed
Substitute 67.76 sec for t in equation (3).
Therefore, the maximum speed
(c)
The maximum altitude
Answer to Problem 11.182RP
The maximum altitude
Explanation of Solution
Given information:
The x coordinate is defined by the relation as
The y coordinate is defined by the relation as
Calculation:
Calculate the maximum altitude
Refer Figure 2, the maximum altitude 600m at time 40 sec.
Substitute 40 sec in equation (2).
Calculate the horizontal
Substitute 80 sec for t in equation (1).
Therefore, the maximum altitude
Want to see more full solutions like this?
Chapter 11 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- 2. Consider the rod with an elliptical that strain 4 a Cross secton considered in class, Integrate the was displacement displacements, relations to obtain thearrow_forwardPlease answer Oxygen at 300 kPa and 90°C flowing at an average velocity of 3 m/s is expanded in an adiabatic nozzle. What is the maximum velocity of the oxygen at the outlet of this nozzle when the outlet pressure is 60 kPa? Use the table containing the ideal gas specific heats of various common gases. The maximum velocity of the oxygen at the outlet of this nozzle is 532.5 Numeric ResponseEdit Unavailable. 532.5 incorrect.m/s.arrow_forwardA container filled with 70 kg of liquid water at 95°C is placed in a 90-m3 room that is initially at 12°C. Thermal equilibrium is established after a while as a result of heat transfer between the water and the air in the room. Assume the room is at the sea level, well sealed, and heavily insulated. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the amount of heat transfer between the water and the air in the room. The amount of heat transfer between the water and the air in the room is kJ.arrow_forward
- A strain gauge rosette that is attached to the surface of a stressed component gives 3 readings (ɛa = A, b = B, &c = C). If the strain gauge rosette is of the D° type (indicating the angle between each of the gauges), construct a Mohr's Strain Circle overleaf. You should assume that gauge A is aligned along the x-axis. Using the Mohr's Strain Circle calculate the: (i) principal strains (ε1, 2)? (ii) principal angles (1, 2)? You should measure these anticlockwise from the y-axis. (iii) maximum shear strain in the plane (ymax)?arrow_forwardQ1. If the yield stress (σy) of a material is 375MPa, determine whether yield is predicted for the stresses acting on both the elements shown below using: (a) Tresca Criterion (b) Von Mises Criterion P Element A R S Element B Note: your values for P (vertical load on Element A) should be negative (i.e. corresponding to a compressive vertical load).arrow_forwardQ. After a puncture a driver is attempting to remove a wheel nut by applying a force of P KN to one end of a wheel brace as shown in Fig. 1. In cross-section the brace is a hollow steel tube (see section aa) of internal diameter r mm and external diameter q mm. wheel nut n Position S P m r q Section aa Fig, 1 (a) Calculate (i) the twisting moment, (ii) the bending moment, and (iii) the shear force in the brace at position S due to the applied load P. (b) Calculate (i) the shear stress due to twisting, and (ii) the bending stress at position S. Note that the shear force will not produce any shear stress at S. (c) Calculate the maximum shearing stress in the brace at position S using the Maximum Shear Stress Criterion. 2 Mechanics of Materials 2 Tutorials Portfolio: Exercise 5 (d) If the maximum permissible shear stress in the steel is 200 MPa, determine the maximum torque that can be applied by the brace without the risk of failure at S.arrow_forward
- Calculate the first 5 Fourier series coefficients (A0-4 and B1-5 ) for the estimated R wave.arrow_forwardRefrigerant-134a is expanded isentropically from 600 kPa and 70°C at the inlet of a steady-flow turbine to 100 kPa at the outlet. The outlet area is 1 m2, and the inlet area is 0.5 m2. Calculate the inlet and outlet velocities when the mass flow rate is 0.65 kg/s. Use the tables for R-134a. The inlet velocity is m/s. The outlet velocity is m/s.arrow_forwardA container filled with 70 kg of liquid water at 95°C is placed in a 90-m3 room that is initially at 12°C. Thermal equilibrium is established after a while as a result of heat transfer between the water and the air in the room. Assume the room is at the sea level, well sealed, and heavily insulated. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the final equilibrium temperature. Use the table containing the ideal gas specific heats of various common gases. The final equilibrium temperature is °C.arrow_forward
- Steam at 100 psia and 650°F is expanded adiabatically in a closed system to 10 psia. Determine the work produced, in Btu/lbm, and the final temperature of steam for an isentropic expansion efficiency of 80 percent. Use steam tables. The work produced is Btu/lbm. The final temperature of steam is °F.arrow_forwardComplet the solution : Vavg Ti Te Ts Q hexp Nuexp htheo Re Nutheo Error (m/s) (*C) (*C) (*C) (W) 2.11 18.8 21.3 45.8 2.61 18.5 20.8 46.3arrow_forwardA 48-kg iron block and a 76-kg copper block, both initially at 80°C, are dropped into a large lake at 15°C. Thermal equilibrium is established after a while as a result of heat transfer between the blocks and the lake water. Determine the total entropy change for this process. The specific heat of iron at room temperature is cp = 0.45 kJ/kg·K. The specific heat of copper at 27°C is cp = 0.386 kJ/kg·K. The total entropy change for this process is kJ/K.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





