ENGINEERING MECHANICS: STATICS
14th Edition
ISBN: 9780135681879
Author: HIBBELER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10.8, Problem 100P
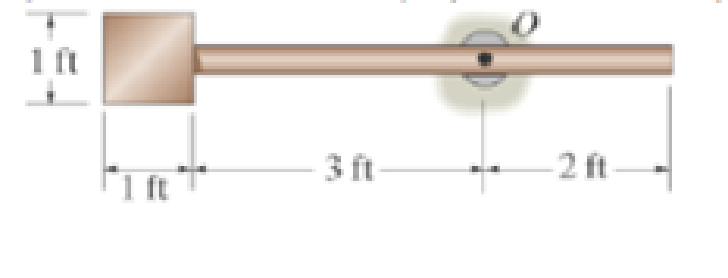
The pendulum consists of a plate having a weight of 12 lb and a slender rod having a weight of 4 lb. Determine the radius of gyration of the pendulum about an axis perpendicular to the page and passing through point O.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The pendulum is suspended from point O and consists of two bars, each weighing 10 lb. Determine the moment of inertia of the pendulum about the axis through the center of mass G.
The pendulum is suspended from point O and consists of two bars, each weighing 10 lb. Determine the moment of inertia of the pendulum about the axis through pin O.
The pendulum consists of a 6.5- kg circular plate and a 2.5- kg slender rod.
Determine the radius of gyration of the pendulum about an axis perpendicular to the page and passing through point O.
Chapter 10 Solutions
ENGINEERING MECHANICS: STATICS
Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of Inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...
Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Solve the problem in two ways, using rectangular...Ch. 10.3 - Determine the moment of inertia of the area about...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Prob. 23PCh. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine me moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - The moment of inertia about the y axis is 264...Ch. 10.4 - Determine the location y of the centroid of the...Ch. 10.4 - Determine,y, which locates the centroidal axis x...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine, g, which locates the centroidal axis z...Ch. 10.4 - Determine the moment of inertia about the x axis.Ch. 10.4 - Prob. 37PCh. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Prob. 40PCh. 10.4 - Prob. 41PCh. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Prob. 43PCh. 10.4 - Prob. 44PCh. 10.4 - Determine the distance x to the centroid C of the...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Prob. 50PCh. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.7 - Determine the product of inertia of the thin strip...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the shaded...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the parabolic...Ch. 10.7 - Prob. 59PCh. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Prob. 61PCh. 10.7 - Prob. 62PCh. 10.7 - Prob. 63PCh. 10.7 - Determine the product of inertia for the beams...Ch. 10.7 - Determine the product of inertia tor the shaded...Ch. 10.7 - Determine the product of inertia of the cross...Ch. 10.7 - Determine the location (xy) to the centroid C of...Ch. 10.7 - For the calculation, assume all comers to be...Ch. 10.7 - Determine the moments of inertia Iu, Iv and the...Ch. 10.7 - Prob. 70PCh. 10.7 - using Mohrs circle Hint. To solve find the...Ch. 10.7 - Prob. 72PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 74PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 76PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 78PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 80PCh. 10.7 - Solve Prob. 10-80 using Mohrs circle.Ch. 10.7 - Prob. 82PCh. 10.7 - Solve Prob. 10-82 using Mohrs circle.Ch. 10.8 - Determine the moment of inertia of the thin ring...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Determine the radius of gyration kx of the...Ch. 10.8 - Prob. 87PCh. 10.8 - Hint: For integration, use thin plate elements...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Prob. 90PCh. 10.8 - Determine the moment of inertia Iy. The specific...Ch. 10.8 - Prob. 92PCh. 10.8 - Prob. 93PCh. 10.8 - The total mass of the solid is 1500 kg.Ch. 10.8 - The slender rods have a mass of 4 kg/ point A....Ch. 10.8 - and a 4-kg slender rod. Determine the radius of...Ch. 10.8 - The material has a density of 200kg/m3. Prob....Ch. 10.8 - Determine the location y of the center of mass G...Ch. 10.8 - Prob. 99PCh. 10.8 - The pendulum consists of a plate having a weight...Ch. 10.8 - 15 lb. and 20 lb, respectively, determine the mass...Ch. 10.8 - The density of the material is 7.85 Mg/m3.Ch. 10.8 - Prob. 103PCh. 10.8 - Determine its mass moment of inertia about the y...Ch. 10.8 - Prob. 105PCh. 10.8 - Prob. 106PCh. 10.8 - Prob. 107PCh. 10.8 - The thin plate has a mass of 12 kg/m2. Determine...Ch. 10.8 - The material has a density of 200kg/m3.Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the area moment of inertia of the shaded...Ch. 10.8 - Prob. 4RPCh. 10.8 - Determine the area moment of inertia of the...Ch. 10.8 - Determine the product of inertia of the shaded...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 3. The pendulum consists of a 5 kg plate and a 3 kg slender rod. Determine the radius of gyration of the pendulum about an axis perpendicular to the plane of movement and passing through point G (the mass center for the pendulum). 2 m + 0.5 m Garrow_forward5kg plate, and 3 kg slender rod. FIND, the radius of gyration of the pendulum about an axis perpendicular to the screen and passing through the point G.arrow_forwardThe pendulum is made up of a plate weighing 10 lb and a bar weighing 4 lb. Determine the radius of gyration of the pendulum about an axis perpendicular to the page through point O. 1 pie -1 pie 3 pies (Hibbeler 17-16) -2 pies-arrow_forward
- Kindly show you handwritten solution. thankyouarrow_forwardThe uniform rod of length 4b and mass m is bent into the shape shown. The diameter of the rod is small compared with its length. Determine the moments of inertia of the rod about the three coordinate axes. Use the values m = 7.9 kg and b = 485 mm. Answers: 1xxx = i lyy= i Izz = i kg.m² kg-m² kg-m²arrow_forwardSlender rod with mass of 2 kg. and cicular plate with mass of 4 kg. FIND, the pendulum radius of gyration about an axis perpendicular to the screen passing through point Oarrow_forward
- The passengers, the ship and the structure have a total mass of 73 Tons, their center of mass in G, and a radius of gyration with respect to B of kB = 3.5 m. Additionally, the 3-ton steel block at point A can be considered as a point of concentrated mass. If the ship rotates freely at 9.3 rad/s when it reaches the lowest point, as shown in the figure, determine the moment of inertia of the system about pivot B (in kgm2) The angular acceleration for the position shown (in rad/s2) is: The vertical reaction at pivot B (in N) is: The horizontal reaction at pivot B (in N) is:arrow_forwardThe uniform rod of length 4b and mass m is bent into the shape shown. The diameter of the rod is small compared with its length. Determine the moments of inertia of the rod about the three coordinate axes. Use the values m = 9.7 kg and b = 650 mm. Answers: Ixx = i lyy= Izz i i kg-m² kg.m² kg.m²arrow_forwardThe pendulum consists of the 3-kg slender rod and the 5-kg thin plate. Determine the location ỹ of the center of mass G of the pendulum; then calculate the moment of inertia of the pendulum about an axis perpendicular to the page and passing through G. y 2 m G 0.5 m Eim-arrow_forward
- 2. Determine the radius of gyration kz for the column's cross-sectional area. 4d The dimension d is given. 2d 4d 4d 4d Zarrow_forwardh y g(x) density p = 800 kg m³ Determine the cone's radius of gyration about the x-axis. 2h x An engineering student has modelled a truncated cone in CAD software by rotating the coloured area about the x-axis. The y-coordinate can be described by the equation g(x) = + 1 and the cup has constant 6 The cone has dimensions h = 1 m and l = 6 m. Xarrow_forwardhe assembly consists of a disk having a mass of 5 kg and slender rods ABand DC which have a mass of 2 kg/m. If L = 0.6 m, determine the moment of inertia and radius of gyration of the assembly about an axis perpendicular to the page and passing through point O. Also, find the position of the center of mass Gin relation to O. Please explain stepsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Ch 2 - 2.2.2 Forced Undamped Oscillation; Author: Benjamin Drew;https://www.youtube.com/watch?v=6Tb7Rx-bCWE;License: Standard youtube license