Chapter 10.3, Problem 82AE

In Problems 79-83, use the fact that the orbit of a planet about the Sun is an ellipse, with the Sun at one focus. The aphelion of a planet is its greatest distance from the Sun, and the perihelion is its shortest distance. The mean distance of a planet from the Sun is the length of the semimajor axis of the elliptical orbit. See the illustration.

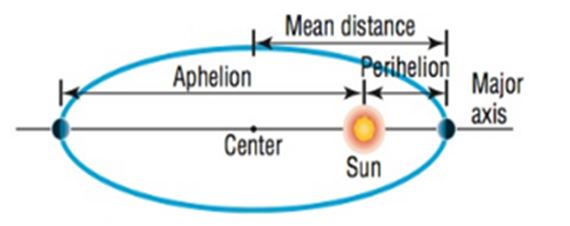
Pluto The perihelion of Pluto is 4551 million miles, and the distance from the center of its elliptical orbit to the Sun is $897.5$ million miles. Find the aphelion of Pluto. What is the mean distance of Pluto from the Sun? Write an equation for the orbit of Pluto about the Sun.