WEBASSIGN F/EPPS DISCRETE MATHEMATICS
5th Edition
ISBN: 9780357540244
Author: EPP
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.3, Problem 12ES
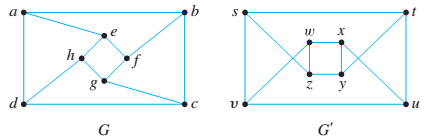
For each pair of simple graphs G and
12. 
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
I need help explaining on this example on how can I define the Time-Domain Function, Apply the Laplace Transformation Formula, and Simplify to Find the Frequency-Domain Expression. I need to understand on finding Y(s)
1. A bicyclist is riding their bike along the Chicago Lakefront Trail. The velocity (in
feet per second) of the bicyclist is recorded below. Use (a) Simpson's Rule, and (b)
the Trapezoidal Rule to estimate the total distance the bicyclist traveled during the
8-second period.
t
0 2
4 6 8
V
10 15
12 10 16
2. Find the midpoint rule approximation for
(a) n = 4
+5
x²dx using n subintervals.
1° 2
(b) n = 8
36
32
28
36
32
28
24
24
20
20
16
16
12
8-
4
1
2
3
4
5
6
12
8
4
1
2
3
4
5
6
1. A Blue Whale's resting heart rate has period that happens to be approximately equal to 2π. A typical ECG of a whale's heartbeat
over one period may be approximated by the function,
f(x)
=
0.005x4
2
0.005x³-0.364x² + 1.27x
on the interval [0, 27]. Find an nth-order Fourier approximation to the Blue Whale's heartbeat, where n ≥ 3 is different from
that used in any other posts on this topic, to generate a periodic function that can be used to model its heartbeat, and graph your
result. Be sure to include your chosen value of n in your Subject Heading.
Chapter 10 Solutions
WEBASSIGN F/EPPS DISCRETE MATHEMATICS
Ch. 10.1 - Let G be a graph and let v and w be vertices in G....Ch. 10.1 - A graph is connected if, any only if, _____.Ch. 10.1 - Removing an edge from a circuit in a graph does...Ch. 10.1 - An Euler circuit in graph is _____.Ch. 10.1 - Prob. 5TYCh. 10.1 - Prob. 6TYCh. 10.1 - Prob. 7TYCh. 10.1 - If a graph G has a Hamiltonian circuit, then G has...Ch. 10.1 - A travelling salesman problem involves finding a...Ch. 10.1 - In the graph below, determine whether the...
Ch. 10.1 - In the graph below, determine whether the...Ch. 10.1 - Let G be the graph and consider the walk...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - An edge whose removal disconnects the graph of...Ch. 10.1 - Given any positive integer n, (a) find a connected...Ch. 10.1 - Find the number of connected components for each...Ch. 10.1 - Each of (a)—(c) describes a graph. In each case...Ch. 10.1 - Prob. 10ESCh. 10.1 - Is it possible for a citizen of Königsberg to make...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Is it possible to take a walk around the city...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - Prob. 20ESCh. 10.1 - Prob. 21ESCh. 10.1 - Prob. 22ESCh. 10.1 - Prob. 23ESCh. 10.1 - Find the complement of each of the following...Ch. 10.1 - Find the complement of the graph K4, the complete...Ch. 10.1 - Suppose that in a group of five people A,B,C,D,...Ch. 10.1 - Prob. 27ESCh. 10.1 - Show that at a party with at least two people,...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Prob. 31ESCh. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - Prob. 33ESCh. 10.1 - Prob. 34ESCh. 10.1 - Prob. 35ESCh. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - Prob. 37ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - Prob. 39ESCh. 10.1 - Prob. 40ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - A traveler in Europe wants to visit each of the...Ch. 10.1 - a. Prove that if a walk in a graph contains a...Ch. 10.1 - Prob. 44ESCh. 10.1 - Prob. 45ESCh. 10.1 - Prob. 46ESCh. 10.1 - Prove that if there is a trail in a graph G from a...Ch. 10.1 - If a graph contains a circuits that starts and...Ch. 10.1 - Prob. 49ESCh. 10.1 - Let G be a connected graph, and let C be any...Ch. 10.1 - Prob. 51ESCh. 10.1 - Prob. 52ESCh. 10.1 - For what values of n dies the complete graph Kn...Ch. 10.1 - For what values of m and n does the complete...Ch. 10.1 - What is the maximum number of edges a simple...Ch. 10.1 - Prob. 56ESCh. 10.1 - Prob. 57ESCh. 10.2 - In the adjacency matrix for a directed graph, the...Ch. 10.2 - Prob. 2TYCh. 10.2 - Prob. 3TYCh. 10.2 - Prob. 4TYCh. 10.2 - Prob. 5TYCh. 10.2 - Prob. 6TYCh. 10.2 - Find real numbers a, b, and c such that the...Ch. 10.2 - Find the adjacency matrices for the following...Ch. 10.2 - Find directed graphs that have the following...Ch. 10.2 - Find adjacency matrices for the following...Ch. 10.2 - Find graphs that have the following adjacency...Ch. 10.2 - Prob. 6ESCh. 10.2 - Prob. 7ESCh. 10.2 - Prob. 8ESCh. 10.2 - Prob. 9ESCh. 10.2 - Prob. 10ESCh. 10.2 - Prob. 11ESCh. 10.2 - Prob. 12ESCh. 10.2 - Let O denote the matrix [0000] . Find 2 × 2...Ch. 10.2 - Prob. 14ESCh. 10.2 - Prob. 15ESCh. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - Prob. 17ESCh. 10.2 - Prob. 18ESCh. 10.2 - Prob. 19ESCh. 10.2 - The following is an adjacency matrix for a graph:...Ch. 10.2 - Let A be the adjacency matrix for K3, the complete...Ch. 10.2 - Draw a graph that has [0001200011000211120021100]...Ch. 10.2 - Prob. 23ESCh. 10.3 - If G and G’ are graphs, then G is isomorphic to G’...Ch. 10.3 - A property P is an invariant for graph isomorphism...Ch. 10.3 - Prob. 3TYCh. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G in 1—5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Prob. 9ESCh. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of simple graphs G and G in 6—13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Draw all nonisomorphic simple graphs with three...Ch. 10.3 - Draw all nonisomorphic simple graphs with four...Ch. 10.3 - Prob. 16ESCh. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Prob. 19ESCh. 10.3 - Draw four nonisomorphic graphs with six vertices,...Ch. 10.3 - Prob. 21ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 23ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 25ESCh. 10.3 - Prob. 26ESCh. 10.3 - Prob. 27ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 29ESCh. 10.3 - Show that the following two graphs are not...Ch. 10.4 - A circuit-free graph is a graph with __________.Ch. 10.4 - Prob. 2TYCh. 10.4 - Prob. 3TYCh. 10.4 - Prob. 4TYCh. 10.4 - Prob. 5TYCh. 10.4 - Prob. 6TYCh. 10.4 - For any positive integer n, if G is a connected...Ch. 10.4 - Read the tree in Example 10.4.2 from left to right...Ch. 10.4 - Prob. 2ESCh. 10.4 - Prob. 3ESCh. 10.4 - Prob. 4ESCh. 10.4 - Prob. 5ESCh. 10.4 - Prob. 6ESCh. 10.4 - Prob. 7ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 14ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 17ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - A connected graph has twelve vertices and eleven...Ch. 10.4 - A connected graph has nine vertices and twelve...Ch. 10.4 - Prob. 24ESCh. 10.4 - Prob. 25ESCh. 10.4 - If a graph has n vertices and n2 or fewer can it...Ch. 10.4 - A circuit-free graph has ten vertices and nine...Ch. 10.4 - Is a circuit-free graph with n vertices and at...Ch. 10.4 - Prob. 29ESCh. 10.4 - Prob. 30ESCh. 10.4 - a. Prove that the following is an invariant for...Ch. 10.5 - Prob. 1TYCh. 10.5 - Prob. 2TYCh. 10.5 - Prob. 3TYCh. 10.5 - Prob. 4TYCh. 10.5 - Prob. 5TYCh. 10.5 - Prob. 1ESCh. 10.5 - Prob. 2ESCh. 10.5 - Draw binary trees to represent the following...Ch. 10.5 - Prob. 4ESCh. 10.5 - Prob. 5ESCh. 10.5 - Prob. 6ESCh. 10.5 - Prob. 7ESCh. 10.5 - Prob. 8ESCh. 10.5 - Prob. 9ESCh. 10.5 - Prob. 10ESCh. 10.5 - Prob. 11ESCh. 10.5 - Prob. 12ESCh. 10.5 - Prob. 13ESCh. 10.5 - Prob. 14ESCh. 10.5 - Prob. 15ESCh. 10.5 - Prob. 16ESCh. 10.5 - Prob. 17ESCh. 10.5 - Prob. 18ESCh. 10.5 - Prob. 19ESCh. 10.5 - Prob. 20ESCh. 10.5 - Prob. 21ESCh. 10.5 - Prob. 22ESCh. 10.5 - Prob. 23ESCh. 10.5 - Prob. 24ESCh. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.6 - Prob. 1TYCh. 10.6 - Prob. 2TYCh. 10.6 - Prob. 3TYCh. 10.6 - In Kruskal’s algorithm, the edges of a connected,...Ch. 10.6 - Prob. 5TYCh. 10.6 - Prob. 6TYCh. 10.6 - At each stage of Dijkstra’s algorithm, the vertex...Ch. 10.6 - Prob. 1ESCh. 10.6 - Prob. 2ESCh. 10.6 - Prob. 3ESCh. 10.6 - Prob. 4ESCh. 10.6 - Prob. 5ESCh. 10.6 - Prob. 6ESCh. 10.6 - Prob. 7ESCh. 10.6 - Prob. 8ESCh. 10.6 - Prob. 9ESCh. 10.6 - Prob. 10ESCh. 10.6 - A pipeline is to be built that will link six...Ch. 10.6 - Use Dijkstra’s algorithm for the airline route...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Prob. 17ESCh. 10.6 - Prob. 18ESCh. 10.6 - Prob. 19ESCh. 10.6 - Prob. 20ESCh. 10.6 - Prob. 21ESCh. 10.6 - Prob. 22ESCh. 10.6 - Prob. 23ESCh. 10.6 - Prob. 24ESCh. 10.6 - Prob. 25ESCh. 10.6 - Prob. 26ESCh. 10.6 - Prob. 27ESCh. 10.6 - Suppose a disconnected graph is input to Kruskal’s...Ch. 10.6 - Suppose a disconnected graph is input to Prim’s...Ch. 10.6 - Modify Algorithm 10.6.3 so that the output...Ch. 10.6 - Prob. 31ES
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- I need help explaining on this example on how can I define the Time-Domain Function, Apply the Laplace Transformation Formula, andarrow_forwardma Classes Term. Spring 2025 Title Details Credit Hours CRN Schedule Type Grade Mode Level Date Status Message *MATHEMATICS FOR MANAGEME... MTH 245, 400 4 54835 Online Normal Grading Mode Ecampus Undergradu... 03/21/2025 Registered **Web Registered... *SOIL SCIENCE CSS 205, 400 0 52298 Online Normal Grading Mode Undergraduate 03/21/2025 Waitlisted Waitlist03/21/2025 PLANT PATHOLOGY BOT 451, 400 4 56960 Online Normal Grading Mode Undergraduate 03/21/2025 Registered **Web Registered... Records: 3 Schedule Schedule Detailsarrow_forwardHere is an augmented matrix for a system of equations (three equations and three variables). Let the variables used be x, y, and z: 1 2 4 6 0 1 -1 3 0 0 1 4 Note: that this matrix is already in row echelon form. Your goal is to use this row echelon form to revert back to the equations that this represents, and then to ultimately solve the system of equations by finding x, y and z. Input your answer as a coordinate point: (x,y,z) with no spaces.arrow_forward
- 1 3 -4 In the following matrix perform the operation 2R1 + R2 → R2. -2 -1 6 After you have completed this, what numeric value is in the a22 position?arrow_forward5 -2 0 1 6 12 Let A = 6 7 -1 and B = 1/2 3 -14 -2 0 4 4 4 0 Compute -3A+2B and call the resulting matrix R. If rij represent the individual entries in the matrix R, what numeric value is in 131? Input your answer as a numeric value only.arrow_forward1 -2 4 10 My goal is to put the matrix 5 -1 1 0 into row echelon form using Gaussian elimination. 3 -2 6 9 My next step is to manipulate this matrix using elementary row operations to get a 0 in the a21 position. Which of the following operations would be the appropriate elementary row operation to use to get a 0 in the a21 position? O (1/5)*R2 --> R2 ○ 2R1 + R2 --> R2 ○ 5R1+ R2 --> R2 O-5R1 + R2 --> R2arrow_forward
- The 2x2 linear system of equations -2x+4y = 8 and 4x-3y = 9 was put into the following -2 4 8 augmented matrix: 4 -3 9 This augmented matrix is then converted to row echelon form. Which of the following matrices is the appropriate row echelon form for the given augmented matrix? 0 Option 1: 1 11 -2 Option 2: 4 -3 9 Option 3: 10 ܂ -2 -4 5 25 1 -2 -4 Option 4: 0 1 5 1 -2 Option 5: 0 0 20 -4 5 ○ Option 1 is the appropriate row echelon form. ○ Option 2 is the appropriate row echelon form. ○ Option 3 is the appropriate row echelon form. ○ Option 4 is the appropriate row echelon form. ○ Option 5 is the appropriate row echelon form.arrow_forwardLet matrix A have order (dimension) 2x4 and let matrix B have order (dimension) 4x4. What results when you compute A+B? The resulting matrix will have dimensions of 2x4. ○ The resulting matrix will be a single number (scalar). The resulting matrix will have dimensions of 4x4. A+B is undefined since matrix A and B do not have the same dimensions.arrow_forwardIf -1 "[a446]-[254] 4b = -1 , find the values of a and b. ○ There is no solution for a and b. ○ There are infinite solutions for a and b. O a=3, b=3 O a=1, b=2 O a=2, b=1 O a=2, b=2arrow_forward
- A student puts a 3x3 system of linear equations is into an augmented matrix. The student then correctly puts the augmented matrix into row echelon form (REF), which yields the following resultant matrix: -2 3 -0.5 10 0 0 0 -2 0 1 -4 Which of the following conclusions is mathematically supported by the work shown about system of linear equations? The 3x3 system of linear equations has no solution. ○ The 3x3 system of linear equations has infinite solutions. The 3x3 system of linear equations has one unique solution.arrow_forwardSolve the following system of equations using matrices: -2x + 4y = 8 and 4x - 3y = 9 Note: This is the same system of equations referenced in Question 14. If a single solution exists, express your solution as an (x,y) coordinate point with no spaces. If there are infinite solutions write inf and if there are no solutions write ns in the box.arrow_forwardHi, I need to make sure I have drafted a thorough analysis, so please answer the following questions. Based on the data in the attached image, develop a regression model to forecast the average sales of football magazines for each of the seven home games in the upcoming season (Year 10). That is, you should construct a single regression model and use it to estimate the average demand for the seven home games in Year 10. In addition to the variables provided, you may create new variables based on these variables or based on observations of your analysis. Be sure to provide a thorough analysis of your final model (residual diagnostics) and provide assessments of its accuracy. What insights are available based on your regression model?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY