Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
3rd Edition
ISBN: 9780134689555
Author: Edgar Goodaire, Michael Parmenter
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10.3, Problem 10E
(a)
To determine
The adjacency matrices
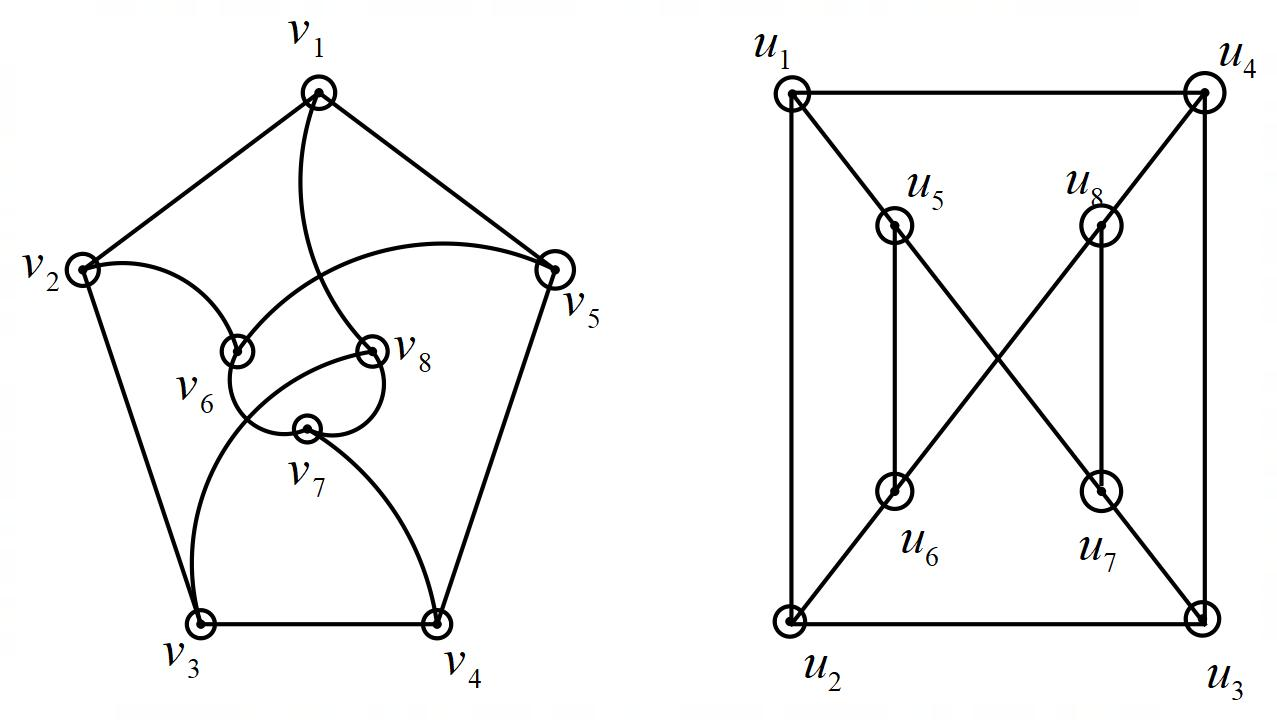
(b)
To determine
The reason that the function
Is an isomorphism.
(c)
To determine
A permutation matrix P that corresponds to the isomorphism in (b) such that
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
2. Let f a function such that f (-2) = 6, f (0) = – 3, ƒ (3) = 0. Give the coordinates of three points on the graph
of y = f(x + 4).
Figure 4 shows the contour map of a function f (x, y) together with a path r(t) in the counterclockwise direction. The points r(l), r(2), and r(3) are indicated on the path. Let g(t) = f (r(t)). Which of statements
Draw the graph of the function f :R → R defined by f (x) = x3, x∈R.
Chapter 10 Solutions
Discrete Mathematics with Graph Theory (Classic Version) (3rd Edition) (Pearson Modern Classics for Advanced Mathematics Series)
Ch. 10.1 - Prob. 1TFQCh. 10.1 - A path is a walk in which all vertices are...Ch. 10.1 - 3. A trail is a path
Ch. 10.1 - A path is trail.Ch. 10.1 - A cycle is a special type of circuit.Ch. 10.1 - 6. A cycle is a circuit with no repeated edges
Ch. 10.1 - 7. An Eulerian circuit is a cycle.
Ch. 10.1 - Prob. 8TFQCh. 10.1 - A sub graph of a connected graph must be...Ch. 10.1 - Prob. 10TFQ
Ch. 10.1 - K8,10 is Eulerian.Ch. 10.1 - Prob. 12TFQCh. 10.1 - 13. A graph with more than one component cannot be...Ch. 10.1 - Prob. 1ECh. 10.1 - [BB] Answer the Konigsberg bridge Problem and...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - 6. Suppose we modify the definition of Eulerian...Ch. 10.1 - 7. (a) Is there an Eulerian trail from A to B in...Ch. 10.1 - [BB] (Fictitious) A recently discovered map of the...Ch. 10.1 - 9. Euler’s original article about the Konigsberg...Ch. 10.1 - Prob. 10ECh. 10.1 - Prob. 11ECh. 10.1 - [BB] For which values of n1 , if any, is Kn...Ch. 10.1 - 13. (a) Find a necessary and sufficient condition...Ch. 10.1 - Prob. 14ECh. 10.1 - 15.[BB] Prove that any circuit in the graph must...Ch. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - 25. Prove that a graph is bipartite if and only if...Ch. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.2 - A Hamiltonian cycle is a circuit.
Ch. 10.2 - Prob. 2TFQCh. 10.2 - Prob. 3TFQCh. 10.2 - Prob. 4TFQCh. 10.2 - Prob. 5TFQCh. 10.2 - A graph that contains a proper cycle cannot be...Ch. 10.2 - Prob. 7TFQCh. 10.2 - Prob. 8TFQCh. 10.2 - Prob. 9TFQCh. 10.2 - Prob. 10TFQCh. 10.2 - Prob. 1ECh. 10.2 - 2. Determine whether or not each of the graphs of...Ch. 10.2 - Determine whether each of the graph shown is...Ch. 10.2 - Prob. 4ECh. 10.2 - Consider the graph shown. Is it Hamiltonian? Is...Ch. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Does the graph have a Hamiltonian cycle that...Ch. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - How many edges must a Hamiltonian cycle is kn...Ch. 10.2 - 12. Draw a picture of a cube, by imagining that...Ch. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Suppose G is a graph with n3 vertices and at least...Ch. 10.2 - 18.[BB] Suppose G is a graph with vertices such...Ch. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Answer true of false and in each case either given...Ch. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Find a necessary and sufficient condition on m and...Ch. 10.3 - Prob. 1TFQCh. 10.3 - Prob. 2TFQCh. 10.3 - Prob. 3TFQCh. 10.3 - Prob. 4TFQCh. 10.3 - Prob. 5TFQCh. 10.3 - Prob. 6TFQCh. 10.3 - Prob. 7TFQCh. 10.3 - Prob. 8TFQCh. 10.3 - Prob. 9TFQCh. 10.3 - Prob. 10TFQCh. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - 8. (a) [BB] Find the adjacency matrices and of...Ch. 10.3 - 9. Repeat Exercise 8 for the graphs and shown....Ch. 10.3 - Prob. 10ECh. 10.3 - Let A=[abcpqrxyz] and let P=[010001100]. Thus P is...Ch. 10.3 - Prob. 12ECh. 10.3 - 13. For each pair of matrices shown, decide...Ch. 10.3 - 14. [BB] Let A be the adjacency matrix of a...Ch. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.4 - Prob. 1TFQCh. 10.4 - Prob. 2TFQCh. 10.4 - It is an open question as to whether there exists...Ch. 10.4 - Prob. 4TFQCh. 10.4 - Prob. 5TFQCh. 10.4 - Prob. 6TFQCh. 10.4 - Prob. 7TFQCh. 10.4 - Prob. 8TFQCh. 10.4 - Prob. 9TFQCh. 10.4 - Prob. 10TFQCh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - 12. [BB] Could Dijkstra’s algorithm (original...Ch. 10.4 - Prob. 13ECh. 10.4 - 14. (a) If weights were assigned to the edges of...Ch. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10 - In the Konigsberg Bringe Problem (see fig. 9.1),...Ch. 10 - Prob. 2RECh. 10 - Suppose G1 and G2 are graphs with no vertices in...Ch. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Is the graph Hamiltonian? Is it Eulerian? Explain...Ch. 10 - Determine, with reason, whether each of the...Ch. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - 15. A connected graph G has 10 vertices and 41...Ch. 10 - Prob. 16RECh. 10 - Let v1,v2,........v8 and w1,w2,..........w12 be...Ch. 10 - Prob. 18RECh. 10 - Martha claims that a graph with adjacency...Ch. 10 - Prob. 20RECh. 10 - Which of the following three matrices (if any) is...Ch. 10 - Apply the first form of Dijkstras algorithm to the...Ch. 10 - Prob. 23RECh. 10 - 24. Apply the original form of Dijkstra’s...Ch. 10 - Apply the improved version of Dijkstras algorithm...Ch. 10 - Prob. 26RECh. 10 - 27. Apply the Floyd- Warshall algorithm apply to...Ch. 10 - Prob. 28RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For the following graphical figure, write the function x(n) and h(n) in: 1. sequential vector 2. functional representation 3. Tabular (3) 2 5 Draw the block diagram of the following function: 1. y(n) = 2x(n-1) 2. y(n) = x(n)/2 + x(n+3)arrow_forwardFor each point on the graph of y= f(x), is a corresponding point on the graph of y=√f(x) exists, determine it. (1, 3) a. (1, 1.73) b. (1, 3) c. Does not exist d. (1,√3)arrow_forwardDetermine whether the functions fi(t) = 2t 5, f2(t) = 2t² +1, f3(t) = 5t² + t are linearly dependent or linearly independent. If they are linearly dependent, find a linear relation among them. W(f1, f2, f3) - = 0 If possible, find c₁, c2, and c3 such that c₁f₁ + C₂f3 + c3f3 = 0 NOTE: Enter an expression in terms of f1, f2, and f3, where not all coefficients are 0. If this is not possible, indicate that using the checkbox. = 0 not possible Therefore, f1, f2, and f3 are linearly dependent.arrow_forward
- Determine whether the functions fi(t) = 4t – 7, f2(t) = 4t² + 1, f3(t) = 7t + t are linearly dependent or linearly independent. If they are linearly dependent, find a linear relation among them. W(fi, f2, f3) = If possible, find c1, c2, and c3 such that cfi + c2f3 + C3f3 = 0 NOTE: Enter an expression in terms of fi, f2, and fs, where not all coefficients are 0. If this is not possible, indicate that using the checkbox. = 0 O not possible Therefore, f1, f2, and f3 are linearly dependent.arrow_forwardUse the given graph of y = f(x) to graph the function g : g(x) = f(x + 1) + 1arrow_forward= mx + b. 4. Let m and b be real numbers, and consider the following three functions: f(x) = 2x + 1, g(x) x + 2, and h(x) A. If function f has a codomain of (5, 7) U (7, 9), the largest its domain can be chosen is (2, 3) U (3, 4). Explain. B. If function g has a codomain of (−1, 1) U (1, 3), the largest its domain can be chosen is (-3, 3) U (3, 9). Explain. C. Within the context of the e- definition of a limit, your result from part A suggests that if € is equal to 2, the largest that can be chosen for function f(x) is 1. Explain. =arrow_forward
- Determine whether the functions fi(t) = 3t – 5, f2(t) = 3t² + 1, f3(t) = 5t +t | are linearly dependent or linearly independent. If they are linearly dependent, find a linear relation among them. W (f1, f2, f3) If possible, find c1, c2, and c3 such that c1fi + c2f3+ c3f3 = 0 NOTE: Enter an expression in terms of f1, f2, and f3, where not all coefficients are 0. If this is not possible, indicate that using the checkbox. = 0 not possible Therefore, f1, f2, and f3 are |Choose onevarrow_forwardLet u and v be the linear functions defined asu(x)=2x+3,v(u)=3x-2.Find the compositions u*v and v*u. Graph the linear functions (u*v)(x)and(v*u)(x)in the same coordinate system.arrow_forward2. Let f(x) = 3x – 7, find a linear function g for which f (g)= I and for which f(g (x)) =x for any number x the function g is: a. g:x →+7. 3 x+7 b. g:x→- 3 7-x c. g:x→ 3 x+7 d. g:x→- 3 x-7 e. g:x→ 3arrow_forward
- Consider the following graph of y = f(x): 40T 20¹ 0 -20+ -40+ -60 6 I only Il only Ill only II and III only I, II, and III 8 10 Which of the following could be the equation for f(x)? I. A+ Ba*, with 0 0, and A 1, B 0, and A < 0.arrow_forwardB2. Write the following beam deflection for a beam of length L = 4 m as a piecewise function y = 2x – x² +(x – 3)³H(x – 3)arrow_forwardLet ƒz = Əƒ/Əz and fz = əƒ/əz. Recall f = u + iv, the notation ƒ is used for the complex conjugate function u iv. Verify the chain rule (fog)z (fog)z = = (fz ○g)9z+(fz° g)āz (fzᵒg) gz+ (fz° g) Izarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Interpolation | Lecture 43 | Numerical Methods for Engineers; Author: Jffrey Chasnov;https://www.youtube.com/watch?v=RpxoN9-i7Jc;License: Standard YouTube License, CC-BY