Chapter 10.2, Problem 84E

  $\left(a\right)$

To determine

To graph: The equation of parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ .

Explanation of Solution

Given information:

The standard form of equation of parabola $x^2=py$ .

Graph:

Consider the standard form of equation of parabola $x^2=py$ .

For $p=1$ , the equation is $x^2=y$ .

For $p=2$ , the equation is $x^2=2y$ .

For $p=3$ , the equation is $x^2=3y$ .

For $p=4$ , the equation is $x^2=4y$ .

On the Cartesian plane plot the parabolas.

The result obtained on screen is provided below,

  

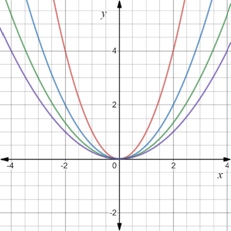
The red curve represents $x^2=y$ , the blue curve represents $x^2=2y$ , green curve represents $x^2=3y$ and purple curve represents $x^2=4y$ .

Interpretation:

As the value of p increase from 1 to 4 the graph becomes wider than the previous one.

  $\left(b\right)$

To determine

To calculate: The focus of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ .

Answer to Problem 84E

The focus of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ is $\left(0,1\right),\left(0,2\right),\left(0,3\right)\text{ and }\left(0,4\right)$ respectively.

Explanation of Solution

Given information:

The standard form of equation of parabola $x^2=py$ .

Formula used:

The focus of the parabola of the form $x^2=py$ is $\left(0,p\right)$ .

Calculation:

Consider the standard form of equation of parabola $x^2=py$ .

For $p=1$ , the equation is $x^2=y$ .

For $p=2$ , the equation is $x^2=2y$ .

For $p=3$ , the equation is $x^2=3y$ .

For $p=4$ , the equation is $x^2=4y$ .

Recall thatfocus of the parabola of the form $x^2=py$ is $\left(0,p\right)$ .

For $p=1$ , the equation is $x^2=y$ and focus is $\left(0,1\right)$ .

For $p=2$ , the equation is $x^2=2y$ and focus is $\left(0,2\right)$ .

For $p=3$ , the equation is $x^2=3y$ and focus is $\left(0,3\right)$

For $p=4$ , the equation is $x^2=4y$ and focus is $\left(0,4\right)$ .

Thus, the focus of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ is $\left(0,1\right),\left(0,2\right),\left(0,3\right)\text{ and }\left(0,4\right)$ respectively.

  $\left(c\right)$

To determine

To calculate: The length of latus rectum of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ .

Answer to Problem 84E

The length of latus rectum of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ is $4,8,12\text{ and }16$ respectively.

Explanation of Solution

Given information:

The standard form of equation of parabola $x^2=py$ .

  

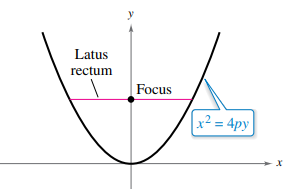
Formula used:

The focus of the parabola of the form $x^2=py$ is $\left(0,p\right)$ .

Calculation:

Consider the standard form of equation of parabola $x^2=py$ .

  

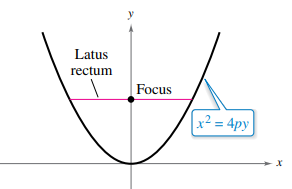
Recall thatfocus of the parabola of the form $x^2=py$ is $\left(0,p\right)$ .

For $p=1$ , the equation is $x^2=y$ and focus is $\left(0,1\right)$ . Search for a point on the parabola that lie on the horizontal line $y=1$ .

  $\begin{array}{c}{x}^2=4y\\ x^2=4\left(1\right)\\ x^2=4\\ x=\pm 2\end{array}$

Therefore, there are two points $\left(2,1\right)\text{ and }\left(-2,1\right)$ with a distance of 4 units between them.

For $p=2$ , the equation is $x^2=2y$ and focus is $\left(0,2\right)$ . Search for a point on the parabola that lie on the horizontal line $y=2$ .

  $\begin{array}{c}{x}^2=8y\\ x^2=8\left(2\right)\\ x^2=16\\ x=\pm 4\end{array}$

Therefore, there are two points $\left(4,2\right)\text{ and }\left(-4,2\right)$ with a distance of 8 units between them.

For $p=3$ , the equation is $x^2=3y$ and focus is $\left(0,3\right)$ . Search for a point on the parabola that lie on the horizontal line $y=3$ .

  $\begin{array}{c}{x}^2=12y\\ x^2=12\left(3\right)\\ x^2=36\\ x=\pm 6\end{array}$

Therefore, there are two points $\left(6,3\right)\text{ and }\left(-6,3\right)$ with a distance of 12 units between them.

For $p=4$ , the equation is $x^2=4y$ and focus is $\left(0,4\right)$ . Search for a point on the parabola that lie on the horizontal line $y=4$ .

  $\begin{array}{c}{x}^2=16y\\ x^2=16\left(4\right)\\ x^2=64\\ x=\pm 8\end{array}$

Therefore, there are two points $\left(8,4\right)\text{ and }\left(-8,4\right)$ with a distance of 16 units between them.

The length of latus rectum of parabola of the form $x^2=py$ is $\left|4p\right|$ .

Thus, the length of latus rectum of the parabola $x^2=py$ for $p=1,p=2,p=3\text{ and }p=4$ is $4,8,12\text{ and }16$ respectively.

  $\left(d\right)$

To determine

To describe: The use of latus rectum to sketch the parabola.

Answer to Problem 84E

The length of latus rectum is used to identity that how narrow or shallow the parabola is.

Explanation of Solution

Given information:

The standard form of equation of parabola $x^2=py$ .

Consider the standard form of equation of parabola $x^2=py$ .

Recall thatfocus of the parabola of the form $x^2=py$ is $\left(0,p\right)$ .

Recall that the length of latus rectum is $\left|4p\right|$ .

The length of latus rectum is used to identity that how narrow or shallow the parabola is.

When a parabola is to be sketched, first plot the vertex and focus of the parabola. Then plot the two points on the parabola that connects the line segment of latus rectum.

At the end join the two points with the vertex to construct the parabola.