
Concept explainers
Suppose that at time zero the can attached to the spring such as shown in Figure 10.8 is released from rest at position x= +A and that its period of vibration is 8.0 s. Draw nine sketches showing the can s approximate position each second starting at 0 s and ending at 8.0 s. Draw and label arrows indicating the relative velocity and acceleration of the can at each position.
Figure 10.8 Dynamics of
(a)
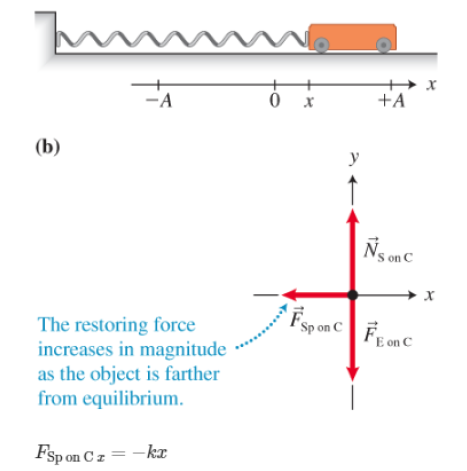
FSpon Cx= -kx
The spring is the only object that exerts a force with a nonzero x-component on the cart. Thus the x-component form of Newton's second (ax−∑Fx/m) becomes
az=kxm=−kmx where m is the mass of the cart. The above expression snows that the carts acceleration ax is proportional to the negative of its displacement x from the equilibrium position This is exactly how the displacement and acceleration of an object undergoing SHM are related [Eq. (10.4)] if the cart is on the positive side of the equilibrium position, the sprig pulls it in the negative direction so that is acceleration component is negative if the cart is on the negative side of the equilibrium position, the spring pushes it n the positive direction so its acceleration component is positive Note that the farther the cart is from equilibrium the greater the magnitude of the force that me spring exerts on the cart and the greater the magnitude of the can s resulting acceleration.
We now understand why the acceleration-versus-time graph in Figure 10.4c is the same shape as the position-versus-time graph in Figure 10.4a with the sign of a being opposite me sign of x at all times the restoring force exerted can the vibrating object is proportional to the displacement of the object from equilibrium but opposite in direction. Whenever this relation holds for a system, that system's motion can be described mathematically as simple harmonic motion.
Stop for a moment and think how unusual Eq. (10.6) is. When we studied linear motion at constant acceleration (Chapter 2 ). the acceleration of a moving object was the same at any location and did not depend on the position When we studied constant speed circular motion (Chapter 5). the direction of acceleration charged with changing positon along the circle. but the magnitude remained the same. In SHM the acceleration of an object changes in time in both magnitude and direction but is synchronized with the displacement of the object Thus the sum of the forces exerted on an object moving in a circle at constant speed is constant in magnitude and only changes direction (it always ports toward the center of the circle). The sum of the forces exerted on an object undergoing SHM not only changes direction during the motion but a so changes magnitude.
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
Modified Mastering Physics with Pearson eText -- Access Card -- for College Physics: Explore and Apply (18-Weeks)
Additional Science Textbook Solutions
Biology: Life on Earth with Physiology (11th Edition)
Microbiology: An Introduction
Cosmic Perspective Fundamentals
Chemistry: Structure and Properties (2nd Edition)
Campbell Biology (11th Edition)
Laboratory Experiments in Microbiology (12th Edition) (What's New in Microbiology)
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





