Understandable Statistics: Concepts And Methods
12th Edition
ISBN: 9781337517508
Author: Charles Henry Brase, Corrinne Pellillo Brase
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10, Problem 6CRP
Before you solve Problems 5–14, first classify the problem as one of the following:
Chi-square test of independence or homogeneity
Chi-square goodness of fit
Chi-square for testing or estimating σ2 or σ
F test for two variances
One-way ANOVA
Two-way ANOVA
Then, in each of the problems when a test is to be performed, do the following:
- (i) Give the value of the level of significance. State the null and alternate hypotheses.
- (ii) Find the sample test statistic.
- (iii) Find or estimate the P-value of the sample test statistic.
- (iv) Conclude the test.
- (v) Interpret the conclusion in the context of the application.
- (vi) In the case of one-way ANOVA, make a summary table.
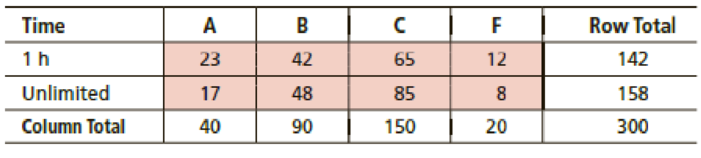
Education: Exams Professor Fair believes that extra time does not improve grades on exams. He randomly divided a group of 300 students into two groups and gave them all the same test. One group had exactly 1 hour in which to finish the test, and the other group could stay as long as desired. The results are shown in the following table. Test at the 0.01 level of significance that time to complete a test and test results are independent.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Consider throwing a die 20 times. Let X be the number of times the
outcome is less than 3. Find the mean X and the variance ož.
(a) 2.22 and 0.33
(b) 4.44 and 6.67
(c) 0.33 and 2.22
(d) 6.67 and 4.44
A population has SS- 100 and variance, o-4. What is the value of x- jal for the population?
O 100
O 400
O 25
A manager believes that the variance of output on the second shift is greater than the variance on the day shift. The following data are collected:
50 samples on the day shift; variance = 500
40 samples on the second shift; variance = 900
Set up hypotheses
Perform a test and state your conclusions.
Chapter 10 Solutions
Understandable Statistics: Concepts And Methods
Ch. 10.1 - Statistical Literacy In general, are chi-square...Ch. 10.1 - Statistical Literacy For chi-square distributions,...Ch. 10.1 - Prob. 3PCh. 10.1 - Prob. 4PCh. 10.1 - Prob. 5PCh. 10.1 - Prob. 6PCh. 10.1 - Prob. 7PCh. 10.1 - Interpretation: Test of Independence Consider...Ch. 10.1 - Prob. 9PCh. 10.1 - For Problems 919, please provide the following...
Ch. 10.1 - Prob. 11PCh. 10.1 - For Problems 919, please provide the following...Ch. 10.1 - Prob. 13PCh. 10.1 - Prob. 14PCh. 10.1 - Prob. 15PCh. 10.1 - Prob. 16PCh. 10.1 - Prob. 17PCh. 10.1 - For Problems 919, please provide the following...Ch. 10.1 - Prob. 19PCh. 10.2 - Statistical Literacy For a chi-square...Ch. 10.2 - Prob. 2PCh. 10.2 - Statistical Literacy Explain why goodness-of-fit...Ch. 10.2 - Prob. 4PCh. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - Prob. 7PCh. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - For Problems 516, please provide the following...Ch. 10.2 - Prob. 14PCh. 10.2 - Prob. 15PCh. 10.2 - Prob. 16PCh. 10.2 - Prob. 17PCh. 10.2 - Prob. 18PCh. 10.3 - Statistical Literacy Does the x distribution need...Ch. 10.3 - Critical Thinking The x distribution must be...Ch. 10.3 - Prob. 3PCh. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - For Problems 311, please provide the following...Ch. 10.3 - Prob. 11PCh. 10.4 - Prob. 1PCh. 10.4 - Statistical Literacy When using the F distribution...Ch. 10.4 - Prob. 3PCh. 10.4 - Prob. 4PCh. 10.4 - Prob. 5PCh. 10.4 - Prob. 6PCh. 10.4 - Prob. 7PCh. 10.4 - Prob. 8PCh. 10.4 - Prob. 9PCh. 10.4 - For Problems 512, please provide the following...Ch. 10.4 - Prob. 11PCh. 10.4 - Prob. 12PCh. 10.5 - In each problem, assume that the distributions are...Ch. 10.5 - Prob. 2PCh. 10.5 - Prob. 3PCh. 10.5 - Prob. 4PCh. 10.5 - Prob. 5PCh. 10.5 - Prob. 6PCh. 10.5 - Prob. 7PCh. 10.5 - Prob. 8PCh. 10.5 - Prob. 9PCh. 10.6 - Prob. 1PCh. 10.6 - Prob. 2PCh. 10.6 - Prob. 3PCh. 10.6 - Prob. 4PCh. 10.6 - Prob. 5PCh. 10.6 - Prob. 6PCh. 10.6 - Prob. 7PCh. 10 - Prob. 1CRPCh. 10 - Prob. 2CRPCh. 10 - Prob. 3CRPCh. 10 - Prob. 4CRPCh. 10 - Prob. 5CRPCh. 10 - Before you solve Problems 514, first classify the...Ch. 10 - Prob. 7CRPCh. 10 - Prob. 8CRPCh. 10 - Prob. 9CRPCh. 10 - Prob. 10CRPCh. 10 - Prob. 11CRPCh. 10 - Prob. 12CRPCh. 10 - Prob. 13CRPCh. 10 - Prob. 14CRPCh. 10 - Prob. 1DHCh. 10 - Prob. 1LCCh. 10 - Prob. 2LCCh. 10 - Prob. 1UTCh. 10 - Prob. 2UTCh. 10 - Prob. 3UT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- The next test is a t-test for unequal variance. Here is the problem: The human resources department at Sue, Grabitt, and Runne also tracks the cost of one-bedroom apartments in two popular neighborhoods, NoBo and SoBo. The general perception of long-time residents is that rents are probably lower in SoBo. They hope to determine whether the average rent for a one-bedroom apartment is lower in SoBo than in NoBo. The results of their survey are shown in Tables 18 and 19: Step 2. Select the Level of Significance, α A 5 percent significance has been selected. Step 3. State the Null Hypothesis (H0) and Alternate Hypothesis (H1) H0: H1: Step 4. Compose the Decision Rule Step 5. Calculate the Value of the Test Statistic, p-value, and estimate statistical power Use G*Power to calculate statistical powerarrow_forwardThe Tukey-Kramer procedure is used for which of the following purposes?A. Test for differences in pairwise means.B. Test for normality of residuals.C. Test for independence of errors.D. Test for homogeneity of variances.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Introduction to experimental design and analysis of variance (ANOVA); Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=vSFo1MwLoxU;License: Standard YouTube License, CC-BY