
Concept explainers
(a)
The rotational kinetic energy.
(a)
Answer to Problem 54P
The rotational kinetic energy for the system is
Explanation of Solution
Redraw the figure P10.54.
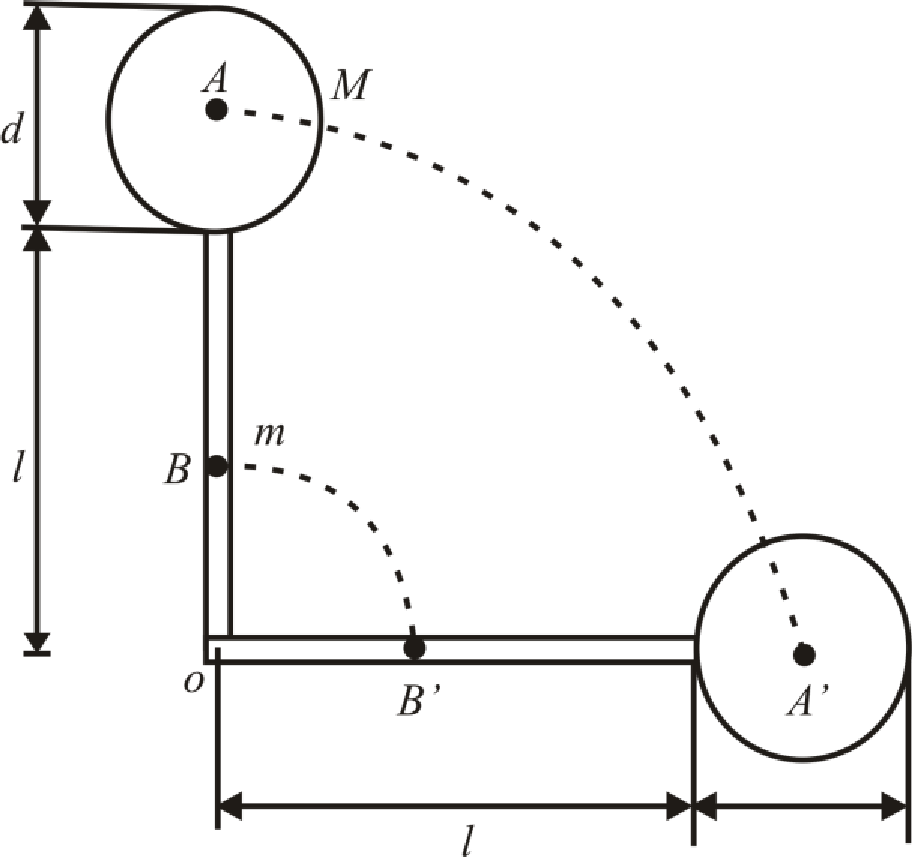
Consider that the vertically standing to be initial position and horizontal to be the final position.
Write the equation for conservation of energy.
Here,
From the law of conservation of energy, gain in rotational kinetic energy equals to loss in gravitational potential energy for the given system.
Write the expression for rotational kinetic energy.
Here,
Write the expression for loss in gravitational potential energy for sphere.
Here,
Write the expression for loss in gravitational potential energy for rod.
Here,
Substitute
Conclusion:
Substitute
Thus, the rotational kinetic energy for the system is
(b)
The angular speed of the rod and ball.
(b)
Answer to Problem 54P
The angular speed of the ball and the rod is
Explanation of Solution
Write the expression for moment of inertia of sphere at center.
Here,
Write the expression for the parallel axis theorem for moment of inertia at point
Here,
Substitute
Write the expression for moment of inertia of rod at point
Here,
Write the expression for net moment of inertia for the whole system.
Here,
Substitute
Write the expression for rotational kinetic energy.
Here,
Simply the above equation for value of
Conclusion:
Substitute
Substitute
Thus, the angular speed of the ball and the rod is
(c)
Thelinear speed of the center of mass of the ball.
(c)
Answer to Problem 54P
The linear speed of the ball of center of mass is
Explanation of Solution
Write the expression for linear speed of the ball.
Here,
Substitute
Here,
Conclusion:
Substitute
Thus, the linear speed of the ball of center of mass is
(d)
Compare the speed with the speed had the ball fallen freelythrough the same distance of
(d)
Answer to Problem 54P
The rod pulls the sphere down together while rotating by the speed factor
Explanation of Solution
Loss in gravitational potential energy will be equal to gain in kinetic energy.
Write the expression for the conservation of energy.
Write the expression for loss in gravitational potential energy for sphere.
Here,
Write the expression for gain kinetic energy.
Here,
Substitute
Write the expression for the ratio of new speed to the original speed.
Here,
Conclusion:
Substitute
Substitute
Thus, the rod pulls the sphere down together while rotating by more speed than in direct falling by the factor of
Want to see more full solutions like this?
Chapter 10 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- (Figure 1)In each case let w be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w Find the direction of the force exerted on the strut by the pivot in the arrangement (a). Express your answer in degrees. Find the tension Tb in the cable in the arrangement (b). Express your answer in terms of w. Find the magnitude of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in terms of w.arrow_forward(Figure 1)In each case let ww be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w. Find the direction of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in degrees.arrow_forwardA 70.0 cm, uniform, 40.0 N shelf is supported horizontally by two vertical wires attached to the sloping ceiling (Figure 1). A very small 20.0 N tool is placed on the shelf midway between the points where the wires are attached to it. Find the tension in the left-hand wire. Express your answer with the appropriate units.arrow_forward
- Find the total bind Mev. binding energy for 13 Carbon, 6C (atomic mass = 13.0033554)arrow_forwardWhat is the 27 energy absorbed in this endothermic Auclear reaction 2] Al + 'n → 27 Mg + ! H? (The atom mass of "Al is 26.981539u. and that of 11 Mg is 26.984341u) MeVarrow_forwardWhat is the energy released in this nuclear reaction 1 F + "', H-1 O+ He? 19 19 16 (The atomic mass of 1F is 18.998403 u, and that of 20 is 15.9949154) MeV.arrow_forward
- What is the energy released in this B+ nuclear reaction خالد 2½ Al w/ Mg + ie? (The atomic mass of 11 Al is 23.9999394 and that > of 12 Mg is 23.985041 u) MeV.arrow_forwardWhat is the energy released / absorbed in this nuclear reaction 14 N+ & He → » O + ! N? (The atomic mass of 14 N is 14.003074u. 17N+ and that of 10 is 16.9991324). MeVarrow_forwardCan someone help me answer this question thanks.arrow_forward
- Can someone help me with this question thanks.arrow_forward4B. Four electrons are located on the corners of a square, one on each corner, with the sides of the square being 25 cm long. a) Draw a sketch of the scenario and use your sketch to b) Determine the total force (magnitude and direction) on one of the electrons from the other three?arrow_forwardPortfolio Problem 3. A ball is thrown vertically upwards with a speed vo from the floor of a room of height h. It hits the ceiling and then returns to the floor, from which it rebounds, managing just to hit the ceiling a second time. Assume that the coefficient of restitution between the ball and the floor, e, is equal to that between the ball and the ceiling. Compute e.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





