Pre-Algebra Student Edition
1st Edition
ISBN: 9780078957734
Author: Glencoe/McGraw-Hill
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10, Problem 40SGR
To determine
To find:the hypotenuse of a right angled
Expert Solution & Answer
Answer to Problem 40SGR
The length of the hypotenuse is 84.85 feet.
Explanation of Solution
Given:
Sidesof a right angled triangle are 60 feet each
Calculation:
The objective is to find the hypotenuse of a right angled triangle whose sides are 60 feet each respectively.
As per the Pythagorean Theorem, in a right angled triangle, the square of the hypotenuse is equal to the sum of the square of legs of the triangle.
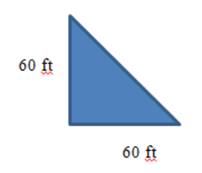
In the given figure the legs are given to be 60 ft each and the hypotenuse is given to be equal to variable c.
Thus from Pythagorean Theorem,
Or,
Or,
Or,
Thus,
The length of the hypotenuse is 84.85 feet.
This will be equal to the distance between two bases diagonally.
Conclusion:
Thus the length of the hypotenuse is 84.85 feet.
Chapter 10 Solutions
Pre-Algebra Student Edition
Ch. 10.1 - Prob. 1AGPCh. 10.1 - Prob. 1BGPCh. 10.1 - Prob. 1CGPCh. 10.1 - Prob. 1DGPCh. 10.1 - Prob. 2AGPCh. 10.1 - Prob. 2BGPCh. 10.1 - Prob. 3AGPCh. 10.1 - Prob. 3BGPCh. 10.1 - Prob. 4AGPCh. 10.1 - Prob. 4BGP
Ch. 10.1 - Prob. 4CGPCh. 10.1 - Prob. 4DGPCh. 10.1 - Prob. 5GPCh. 10.1 - Prob. 1CYUCh. 10.1 - Prob. 2CYUCh. 10.1 - Prob. 3CYUCh. 10.1 - Prob. 4CYUCh. 10.1 - Prob. 5CYUCh. 10.1 - Prob. 6CYUCh. 10.1 - Prob. 7CYUCh. 10.1 - Prob. 8CYUCh. 10.1 - Prob. 9CYUCh. 10.1 - Prob. 10CYUCh. 10.1 - Prob. 11PPSCh. 10.1 - Prob. 12PPSCh. 10.1 - Prob. 13PPSCh. 10.1 - Prob. 14PPSCh. 10.1 - Prob. 15PPSCh. 10.1 - Prob. 16PPSCh. 10.1 - Prob. 17PPSCh. 10.1 - Prob. 18PPSCh. 10.1 - Prob. 19PPSCh. 10.1 - Prob. 20PPSCh. 10.1 - Prob. 21PPSCh. 10.1 - Prob. 22PPSCh. 10.1 - Prob. 23PPSCh. 10.1 - Prob. 24PPSCh. 10.1 - Prob. 25PPSCh. 10.1 - Prob. 26PPSCh. 10.1 - Prob. 27PPSCh. 10.1 - Prob. 28PPSCh. 10.1 - Prob. 29PPSCh. 10.1 - Prob. 30PPSCh. 10.1 - Prob. 31PPSCh. 10.1 - Prob. 32PPSCh. 10.1 - Prob. 33PPSCh. 10.1 - Prob. 34PPSCh. 10.1 - Prob. 35PPSCh. 10.1 - Prob. 36PPSCh. 10.1 - Prob. 37PPSCh. 10.1 - Prob. 38PPSCh. 10.1 - Prob. 39PPSCh. 10.1 - Prob. 40HPCh. 10.1 - Prob. 41HPCh. 10.1 - Prob. 42HPCh. 10.1 - Prob. 43HPCh. 10.1 - Prob. 44STPCh. 10.1 - Prob. 45STPCh. 10.1 - Prob. 46STPCh. 10.1 - Prob. 47STPCh. 10.1 - Prob. 48SRCh. 10.1 - Prob. 49SRCh. 10.1 - Prob. 50SRCh. 10.1 - Prob. 51SRCh. 10.1 - Prob. 52SRCh. 10.1 - Prob. 53SRCh. 10.1 - Prob. 54SRCh. 10.1 - Prob. 55SCh. 10.1 - Prob. 56SCh. 10.1 - Prob. 57SCh. 10.1 - Prob. 58SCh. 10.1 - Prob. 59SCh. 10.1 - Prob. 60SCh. 10.1 - Prob. 61SCh. 10.1 - Prob. 62SCh. 10.2 - Prob. 1AGPCh. 10.2 - Prob. 1BGPCh. 10.2 - Prob. 1CGPCh. 10.2 - Prob. 1DGPCh. 10.2 - Prob. 2GPCh. 10.2 - Prob. 3GPCh. 10.2 - Prob. 4AGPCh. 10.2 - Prob. 4BGPCh. 10.2 - Prob. 5GPCh. 10.2 - Prob. 1CYUCh. 10.2 - Prob. 2CYUCh. 10.2 - Prob. 3CYUCh. 10.2 - Prob. 4CYUCh. 10.2 - Prob. 5CYUCh. 10.2 - Prob. 6CYUCh. 10.2 - Prob. 7CYUCh. 10.2 - Prob. 8CYUCh. 10.2 - Prob. 9CYUCh. 10.2 - Prob. 10CYUCh. 10.2 - Prob. 11CYUCh. 10.2 - Prob. 12CYUCh. 10.2 - Prob. 13CYUCh. 10.2 - Prob. 14PPSCh. 10.2 - Prob. 15PPSCh. 10.2 - Prob. 16PPSCh. 10.2 - Prob. 17PPSCh. 10.2 - Prob. 18PPSCh. 10.2 - Prob. 19PPSCh. 10.2 - Prob. 20PPSCh. 10.2 - Prob. 21PPSCh. 10.2 - Prob. 22PPSCh. 10.2 - Prob. 23PPSCh. 10.2 - Prob. 24PPSCh. 10.2 - Prob. 25PPSCh. 10.2 - Prob. 26PPSCh. 10.2 - Prob. 27PPSCh. 10.2 - Prob. 28PPSCh. 10.2 - Prob. 29PPSCh. 10.2 - Prob. 30PPSCh. 10.2 - Prob. 31PPSCh. 10.2 - Prob. 32PPSCh. 10.2 - Prob. 33PPSCh. 10.2 - Prob. 34PPSCh. 10.2 - Prob. 35PPSCh. 10.2 - Prob. 36PPSCh. 10.2 - Prob. 37PPSCh. 10.2 - Prob. 38PPSCh. 10.2 - Prob. 39PPSCh. 10.2 - Prob. 40PPSCh. 10.2 - Prob. 41PPSCh. 10.2 - Prob. 42PPSCh. 10.2 - Prob. 43PPSCh. 10.2 - Prob. 44PPSCh. 10.2 - Prob. 45PPSCh. 10.2 - Prob. 46PPSCh. 10.2 - Prob. 47PPSCh. 10.2 - Prob. 48PPSCh. 10.2 - Prob. 49PPSCh. 10.2 - Prob. 50PPSCh. 10.2 - Prob. 51PPSCh. 10.2 - Prob. 52PPSCh. 10.2 - Prob. 53HPCh. 10.2 - Prob. 54HPCh. 10.2 - Prob. 55HPCh. 10.2 - Prob. 56HPCh. 10.2 - Prob. 57HPCh. 10.2 - Prob. 58HPCh. 10.2 - Prob. 59HPCh. 10.2 - Prob. 60STPCh. 10.2 - Prob. 61STPCh. 10.2 - Prob. 62STPCh. 10.2 - Prob. 63STPCh. 10.2 - Prob. 64SRCh. 10.2 - Prob. 65SRCh. 10.2 - Prob. 66SRCh. 10.2 - Prob. 67SRCh. 10.2 - Prob. 68SRCh. 10.2 - Prob. 69SRCh. 10.2 - Prob. 70SRCh. 10.2 - Prob. 71SRCh. 10.2 - Prob. 72SRCh. 10.2 - Prob. 73SRCh. 10.2 - Prob. 74SRCh. 10.2 - Prob. 75SCh. 10.2 - Prob. 76SCh. 10.2 - Prob. 77SCh. 10.2 - Prob. 78SCh. 10.2 - Prob. 79SCh. 10.2 - Prob. 80SCh. 10.3 - Prob. 1GPCh. 10.3 - Prob. 2GPCh. 10.3 - Prob. 3GPCh. 10.3 - Prob. 4AGPCh. 10.3 - Prob. 4BGPCh. 10.3 - Prob. 1CYUCh. 10.3 - Prob. 2CYUCh. 10.3 - Prob. 3CYUCh. 10.3 - Prob. 4CYUCh. 10.3 - Prob. 5CYUCh. 10.3 - Prob. 6PPSCh. 10.3 - Prob. 7PPSCh. 10.3 - Prob. 8PPSCh. 10.3 - Prob. 9PPSCh. 10.3 - Prob. 10PPSCh. 10.3 - Prob. 11PPSCh. 10.3 - Prob. 12PPSCh. 10.3 - Prob. 13PPSCh. 10.3 - Prob. 14PPSCh. 10.3 - Prob. 15PPSCh. 10.3 - Prob. 16PPSCh. 10.3 - Prob. 17PPSCh. 10.3 - Prob. 18PPSCh. 10.3 - Prob. 19PPSCh. 10.3 - Prob. 20PPSCh. 10.3 - Prob. 21PPSCh. 10.3 - Prob. 22PPSCh. 10.3 - Prob. 23PPSCh. 10.3 - Prob. 24PPSCh. 10.3 - Prob. 25PPSCh. 10.3 - Prob. 26PPSCh. 10.3 - Prob. 27PPSCh. 10.3 - Prob. 28PPSCh. 10.3 - Prob. 29PPSCh. 10.3 - Prob. 30PPSCh. 10.3 - Prob. 31PPSCh. 10.3 - Prob. 32PPSCh. 10.3 - Prob. 33PPSCh. 10.3 - Prob. 34PPSCh. 10.3 - Prob. 35HPCh. 10.3 - Prob. 36HPCh. 10.3 - Prob. 37HPCh. 10.3 - Prob. 38HPCh. 10.3 - Prob. 39HPCh. 10.3 - Prob. 40STPCh. 10.3 - Prob. 41STPCh. 10.3 - Prob. 42STPCh. 10.3 - Prob. 43STPCh. 10.3 - Prob. 44SRCh. 10.3 - Prob. 45SRCh. 10.3 - Prob. 46SRCh. 10.3 - Prob. 47SRCh. 10.3 - Prob. 48SRCh. 10.3 - Prob. 49SRCh. 10.3 - Prob. 50SRCh. 10.3 - Prob. 51SRCh. 10.3 - Prob. 52SRCh. 10.3 - Prob. 53SCh. 10.3 - Prob. 54SCh. 10.3 - Prob. 55SCh. 10.3 - Prob. 56SCh. 10.4 - Prob. 1GPCh. 10.4 - Prob. 2GPCh. 10.4 - Prob. 3GPCh. 10.4 - Prob. 4AGPCh. 10.4 - Prob. 4BGPCh. 10.4 - Prob. 1CYUCh. 10.4 - Prob. 2CYUCh. 10.4 - Prob. 3CYUCh. 10.4 - Prob. 4CYUCh. 10.4 - Prob. 5CYUCh. 10.4 - Prob. 6CYUCh. 10.4 - Prob. 7CYUCh. 10.4 - Prob. 8CYUCh. 10.4 - Prob. 9PPSCh. 10.4 - Prob. 10PPSCh. 10.4 - Prob. 11PPSCh. 10.4 - Prob. 12PPSCh. 10.4 - Prob. 13PPSCh. 10.4 - Prob. 14PPSCh. 10.4 - Prob. 15PPSCh. 10.4 - Prob. 16PPSCh. 10.4 - Prob. 17PPSCh. 10.4 - Prob. 18PPSCh. 10.4 - Prob. 19PPSCh. 10.4 - Prob. 20PPSCh. 10.4 - Prob. 21PPSCh. 10.4 - Prob. 22PPSCh. 10.4 - Prob. 23PPSCh. 10.4 - Prob. 24PPSCh. 10.4 - Prob. 25PPSCh. 10.4 - Prob. 26PPSCh. 10.4 - Prob. 27PPSCh. 10.4 - Prob. 28PPSCh. 10.4 - Prob. 29PPSCh. 10.4 - Prob. 30PPSCh. 10.4 - Prob. 31PPSCh. 10.4 - Prob. 32PPSCh. 10.4 - Prob. 33PPSCh. 10.4 - Prob. 34HPCh. 10.4 - Prob. 35HPCh. 10.4 - Prob. 36HPCh. 10.4 - Prob. 37HPCh. 10.4 - Prob. 38HPCh. 10.4 - Prob. 39STPCh. 10.4 - Prob. 40STPCh. 10.4 - Prob. 41STPCh. 10.4 - Prob. 42STPCh. 10.4 - Prob. 43SRCh. 10.4 - Prob. 44SRCh. 10.4 - Prob. 45SRCh. 10.4 - Prob. 46SRCh. 10.4 - Prob. 47SRCh. 10.4 - Prob. 48SRCh. 10.4 - Prob. 49SRCh. 10.4 - Prob. 50SRCh. 10.4 - Prob. 51SCh. 10.4 - Prob. 52SCh. 10.4 - Prob. 53SCh. 10.5 - Prob. 1GPCh. 10.5 - Prob. 2GPCh. 10.5 - Prob. 3GPCh. 10.5 - Prob. 1CYUCh. 10.5 - Prob. 2CYUCh. 10.5 - Prob. 3CYUCh. 10.5 - Prob. 4CYUCh. 10.5 - Prob. 5CYUCh. 10.5 - Prob. 6PPSCh. 10.5 - Prob. 7PPSCh. 10.5 - Prob. 8PPSCh. 10.5 - Prob. 9PPSCh. 10.5 - Prob. 10PPSCh. 10.5 - Prob. 11PPSCh. 10.5 - Prob. 12PPSCh. 10.5 - Prob. 13PPSCh. 10.5 - Prob. 14PPSCh. 10.5 - Prob. 15PPSCh. 10.5 - Prob. 16PPSCh. 10.5 - Prob. 17PPSCh. 10.5 - Prob. 18PPSCh. 10.5 - Prob. 19PPSCh. 10.5 - Prob. 20PPSCh. 10.5 - Prob. 21PPSCh. 10.5 - Prob. 22PPSCh. 10.5 - Prob. 23PPSCh. 10.5 - Prob. 24PPSCh. 10.5 - Prob. 25PPSCh. 10.5 - Prob. 26PPSCh. 10.5 - Prob. 27HPCh. 10.5 - Prob. 28HPCh. 10.5 - Prob. 29HPCh. 10.5 - Prob. 30HPCh. 10.5 - Prob. 31HPCh. 10.5 - Prob. 32STPCh. 10.5 - Prob. 33STPCh. 10.5 - Prob. 34STPCh. 10.5 - Prob. 35STPCh. 10.5 - Prob. 36SRCh. 10.5 - Prob. 37SRCh. 10.5 - Prob. 38SRCh. 10.5 - Prob. 39SRCh. 10.5 - Prob. 40SCh. 10.5 - Prob. 41SCh. 10.5 - Prob. 42SCh. 10.6 - Prob. 1GPCh. 10.6 - Prob. 2GPCh. 10.6 - Prob. 3GPCh. 10.6 - Prob. 1CYUCh. 10.6 - Prob. 2CYUCh. 10.6 - Prob. 3CYUCh. 10.6 - Prob. 4CYUCh. 10.6 - Prob. 5CYUCh. 10.6 - Prob. 6CYUCh. 10.6 - Prob. 7CYUCh. 10.6 - Prob. 8CYUCh. 10.6 - Prob. 9PPSCh. 10.6 - Prob. 10PPSCh. 10.6 - Prob. 11PPSCh. 10.6 - Prob. 12PPSCh. 10.6 - Prob. 13PPSCh. 10.6 - Prob. 14PPSCh. 10.6 - Prob. 15PPSCh. 10.6 - Prob. 16PPSCh. 10.6 - Prob. 17PPSCh. 10.6 - Prob. 18PPSCh. 10.6 - Prob. 19PPSCh. 10.6 - Prob. 20PPSCh. 10.6 - Prob. 21PPSCh. 10.6 - Prob. 22PPSCh. 10.6 - Prob. 23HPCh. 10.6 - Prob. 24HPCh. 10.6 - Prob. 25HPCh. 10.6 - Prob. 26HPCh. 10.6 - Prob. 27HPCh. 10.6 - Prob. 28STPCh. 10.6 - Prob. 29STPCh. 10.6 - Prob. 30STPCh. 10.6 - Prob. 31STPCh. 10.6 - Prob. 32SRCh. 10.6 - Prob. 33SRCh. 10.6 - Prob. 34SRCh. 10.6 - Prob. 35SRCh. 10.6 - Prob. 36SRCh. 10.6 - Prob. 37SRCh. 10.6 - Prob. 38SRCh. 10.6 - Prob. 39SRCh. 10.6 - Prob. 40SRCh. 10.6 - Prob. 41SCh. 10.6 - Prob. 42SCh. 10.6 - Prob. 43SCh. 10.6 - Prob. 44SCh. 10.6 - Prob. 45SCh. 10.6 - Prob. 46SCh. 10.6 - Prob. 47SCh. 10.6 - Prob. 48SCh. 10 - Prob. 1QCCh. 10 - Prob. 2QCCh. 10 - Prob. 3QCCh. 10 - Prob. 4QCCh. 10 - Prob. 5QCCh. 10 - Prob. 6QCCh. 10 - Prob. 7QCCh. 10 - Prob. 8QCCh. 10 - Prob. 9QCCh. 10 - Prob. 10QCCh. 10 - Prob. 11QCCh. 10 - Prob. 12QCCh. 10 - Prob. 13QCCh. 10 - Prob. 14QCCh. 10 - Prob. 15QCCh. 10 - Prob. 16QCCh. 10 - Prob. 17QCCh. 10 - Prob. 18QCCh. 10 - Prob. 19QCCh. 10 - Prob. 20QCCh. 10 - Prob. 1MCQCh. 10 - Prob. 2MCQCh. 10 - Prob. 3MCQCh. 10 - Prob. 4MCQCh. 10 - Prob. 5MCQCh. 10 - Prob. 6MCQCh. 10 - Prob. 7MCQCh. 10 - Prob. 8MCQCh. 10 - Prob. 9MCQCh. 10 - Prob. 10MCQCh. 10 - Prob. 11MCQCh. 10 - Prob. 12MCQCh. 10 - Prob. 13MCQCh. 10 - Prob. 14MCQCh. 10 - Prob. 15MCQCh. 10 - Prob. 16MCQCh. 10 - Prob. 17MCQCh. 10 - Prob. 18MCQCh. 10 - Prob. 19MCQCh. 10 - Prob. 20MCQCh. 10 - Prob. 21MCQCh. 10 - Prob. 22MCQCh. 10 - Prob. 23MCQCh. 10 - Prob. 24MCQCh. 10 - Prob. 25MCQCh. 10 - Prob. 26MCQCh. 10 - Prob. 27MCQCh. 10 - Prob. 28MCQCh. 10 - Prob. 29MCQCh. 10 - Prob. 30MCQCh. 10 - Prob. 31MCQCh. 10 - Prob. 32MCQCh. 10 - Prob. 33MCQCh. 10 - Prob. 1SGRCh. 10 - Prob. 2SGRCh. 10 - Prob. 3SGRCh. 10 - Prob. 4SGRCh. 10 - Prob. 5SGRCh. 10 - Prob. 6SGRCh. 10 - Prob. 7SGRCh. 10 - Prob. 8SGRCh. 10 - Prob. 9SGRCh. 10 - Prob. 10SGRCh. 10 - Prob. 11SGRCh. 10 - Prob. 12SGRCh. 10 - Prob. 13SGRCh. 10 - Prob. 14SGRCh. 10 - Prob. 15SGRCh. 10 - Prob. 16SGRCh. 10 - Prob. 17SGRCh. 10 - Prob. 18SGRCh. 10 - Prob. 19SGRCh. 10 - Prob. 20SGRCh. 10 - Prob. 21SGRCh. 10 - Prob. 22SGRCh. 10 - Prob. 23SGRCh. 10 - Prob. 24SGRCh. 10 - Prob. 25SGRCh. 10 - Prob. 26SGRCh. 10 - Prob. 27SGRCh. 10 - Prob. 28SGRCh. 10 - Prob. 29SGRCh. 10 - Prob. 30SGRCh. 10 - Prob. 31SGRCh. 10 - Prob. 32SGRCh. 10 - Prob. 33SGRCh. 10 - Prob. 34SGRCh. 10 - Prob. 35SGRCh. 10 - Prob. 36SGRCh. 10 - Prob. 37SGRCh. 10 - Prob. 38SGRCh. 10 - Prob. 39SGRCh. 10 - Prob. 40SGRCh. 10 - Prob. 41SGRCh. 10 - Prob. 42SGRCh. 10 - Prob. 43SGRCh. 10 - Prob. 44SGRCh. 10 - Prob. 45SGRCh. 10 - Prob. 46SGRCh. 10 - Prob. 47SGRCh. 10 - Prob. 48SGRCh. 10 - Prob. 49SGRCh. 10 - Prob. 50SGRCh. 10 - Prob. 51SGRCh. 10 - Prob. 1PTCh. 10 - Prob. 2PTCh. 10 - Prob. 3PTCh. 10 - Prob. 4PTCh. 10 - Prob. 5PTCh. 10 - Prob. 6PTCh. 10 - Prob. 7PTCh. 10 - Prob. 8PTCh. 10 - Prob. 9PTCh. 10 - Prob. 10PTCh. 10 - Prob. 11PTCh. 10 - Prob. 12PTCh. 10 - Prob. 13PTCh. 10 - Prob. 14PTCh. 10 - Prob. 15PTCh. 10 - Prob. 16PTCh. 10 - Prob. 17PTCh. 10 - Prob. 18PTCh. 10 - Prob. 19PTCh. 10 - Prob. 20PTCh. 10 - Prob. 21PTCh. 10 - Prob. 22PTCh. 10 - Prob. 23PTCh. 10 - Prob. 24PTCh. 10 - Prob. 25PTCh. 10 - Prob. 1ECh. 10 - Prob. 2ECh. 10 - Prob. 1STPCh. 10 - Prob. 2STPCh. 10 - Prob. 3STPCh. 10 - Prob. 4STPCh. 10 - Prob. 5STPCh. 10 - Prob. 6STPCh. 10 - Prob. 7STPCh. 10 - Prob. 8STPCh. 10 - Prob. 9STPCh. 10 - Prob. 10STPCh. 10 - Prob. 11STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
CHECK POINT 1 In a survey on musical tastes, respondents were asked: Do you listed to classical music? Do you l...
Thinking Mathematically (6th Edition)
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
Finding the Margin of Error In Exercises 33 and 34, use the confidence interval to find the estimated margin of...
Elementary Statistics: Picturing the World (7th Edition)
Answer each of the following and explain your answer. a. How many lines can contain a particular segment? b. Ho...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Choose one of the answers in each case. In statistical inference, measurements are made on a (sample or popula...
Introductory Statistics
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Solve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forward
- Dalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1arrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5arrow_forward
- Write an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forwardUse the graph of the polynomial function of degree 5 to identify zeros and multiplicity. Order your zeros from least to greatest. -6 3 6+ 5 4 3 2 1 2 -1 -2 -3 -4 -5 3 4 6 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 5 4 -6-5-4-3-2 3 21 2 1 2 4 5 ૪ 345 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity པ་arrow_forward
- Use the graph to write the formula for a polynomial function of least degree. -5 + 4 3 ♡ 2 12 1 f(x) -1 -1 f(x) 2 3. + -3 12 -5+ + xarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 -6-5-4-3-2-1 -1 -2 3 -4 4 5 6 a Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to write the formula for a polynomial function of least degree. 5 4 3 -5 -x 1 f(x) -5 -4 -1 1 2 3 4 -1 -2 -3 -4 -5 f(x) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY