
Concept explainers
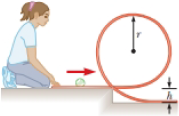
A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4.03 m/s on a horizontal section of a track as shown in Figure P10.33. It rolls around the inside of a vertical circular loop of radius r = 45.0 cm. As the ball nears the bottom of the loop, the shape of the track deviates from a perfect circle so that the ball leaves the track at a point h = 20.0 cm below the horizontal section. (a) Find the ball’s speed at the top of the loop. (b) Demonstrate that the ball will not fall from the track at the top of the loop. (c) Find the ball’s speed as it leaves the track at the bottom. (d) What If? Suppose that static friction between ball and track were negligible so that the ball slid instead of rolling. Describe the speed of the ball at the top of the loop in this situation. (e) Explain your answer to part (d).
Figure P10.33
(a)
The speed of the ball at the top of the loop.
Answer to Problem 10.64P
The speed of the ball at the top of the loop is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the translational kinetic energy of the ball at horizontal track
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Therefore, the speed of the ball at the top of the loop is
(b)
The reason that the ball will not fall from the track at the top of the loop.
Answer to Problem 10.64P
The ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
Explanation of Solution
The radius of the circular loop is
Formula to calculate the centripetal acceleration on the ball at the top of the loop
Here,
Substitute
Thus, the centripetal acceleration act on the ball at the top of the loop is
Since the centripetal acceleration at the top of the loop is more than the acceleration due to gravity that is
Conclusion:
Therefore, the ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
(c)
The speed of the ball as it leaves the track at the bottom.
Answer to Problem 10.64P
The speed of the ball as it leaves the track at the bottom is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the bottom of the loop
Here,
Write the expression for the translational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Thus, the speed of the ball as it leaves the track at the bottom is
(d)
The speed of the ball at the top of the loop if ball slide instead of roll.
Answer to Problem 10.64P
The speed of the ball at the top of the loop is imaginary.
Explanation of Solution
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Write the expression for the new translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the new potential energy of the ball at top point of the loop
Substitute
Simplify the above equation for
Substitute
Since the value inside the square root is negative that means the value is imaginary. This condition is impractical.
Thus, the speed of the ball at the top of the loop is imaginary.
Conclusion:
Therefore, the speed of the ball at the top of the loop is imaginary. It can’t be calculated.
(e)
The explanation of the solution of part (d).
Answer to Problem 10.64P
The ball has not sufficient energy to arrive at top of the circular loop.
Explanation of Solution
The velocity comes out to be imaginary in part (d) that indicates the situation in impossible because as the boll slide instead of rolling, the ball have only translational kinetic energy which is insufficient for the ball to reach the top point on the circular loop.
Thus, the ball did not arrive at the top point of the loop.
Conclusion:
Therefore, the ball has not sufficient energy to arrive at top of the circular loop.
Want to see more full solutions like this?
Chapter 10 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- 3.19 • Win the Prize. In a carnival booth, you can win a stuffed gi- raffe if you toss a quarter into a small dish. The dish is on a shelf above the point where the quarter leaves your hand and is a horizontal dis- tance of 2.1 m from this point (Fig. E3.19). If you toss the coin with a velocity of 6.4 m/s at an angle of 60° above the horizontal, the coin will land in the dish. Ignore air resistance. (a) What is the height of the shelf above the point where the quarter leaves your hand? (b) What is the vertical component of the velocity of the quarter just before it lands in the dish? Figure E3.19 6.4 m/s 2.1arrow_forwardCan someone help me answer this thank you.arrow_forward1.21 A postal employee drives a delivery truck along the route shown in Fig. E1.21. Determine the magnitude and direction of the resultant displacement by drawing a scale diagram. (See also Exercise 1.28 for a different approach.) Figure E1.21 START 2.6 km 4.0 km 3.1 km STOParrow_forward
- help because i am so lost and it should look something like the picturearrow_forward3.31 A Ferris wheel with radius Figure E3.31 14.0 m is turning about a horizontal axis through its center (Fig. E3.31). The linear speed of a passenger on the rim is constant and equal to 6.00 m/s. What are the magnitude and direction of the passenger's acceleration as she passes through (a) the lowest point in her circular motion and (b) the high- est point in her circular motion? (c) How much time does it take the Ferris wheel to make one revolution?arrow_forward1.56 ⚫. Three horizontal ropes pull on a large stone stuck in the ground, producing the vector forces A, B, and C shown in Fig. P1.56. Find the magnitude and direction of a fourth force on the stone that will make the vector sum of the four forces zero. Figure P1.56 B(80.0 N) 30.0 A (100.0 N) 53.0° C (40.0 N) 30.0°arrow_forward
- 1.39 Given two vectors A = -2.00 +3.00 +4.00 and B=3.00 +1.00 -3.00k. (a) find the magnitude of each vector; (b) use unit vectors to write an expression for the vector difference A - B; and (c) find the magnitude of the vector difference A - B. Is this the same as the magnitude of B - Ä? Explain.arrow_forward5. The radius of a circle is 5.5 cm. (a) What is the circumference in meters? (b) What is its area in square meters? 6. Using the generic triangle below, solve the following: 0 = 55 and c = 32 m, solve for a and b. a = 250 m and b = 180 m, solve for the angle and c. b=104 cm and c = 65 cm, solve for a and the angle b a 7. Consider the figure below representing the Temperature (T in degrees Celsius) as a function of time t (in seconds) 4 12 20 (a) What is the area under the curve in the figure below? (b) The area under the graph can be calculated using integrals or derivatives? (c) During what interval is the derivative of temperature with respect to time equal to zero?arrow_forwardPart 3: Symbolic Algebra Often problems in science and engineering are done with variables only. Don't let the different letters confuse you. Manipulate them algebraically as though they were numbers. 1. Solve 3x-7= x + 3 for x 2x-1 2. Solve- for x 2+2 In questions 3-11 solve for the required symbol/letter 3. v2 +2a(s-80), a = = 4. B= Ho I 2π r 5. K = kz² 6.xm= MAL ,d= d 7.T, 2 = 8.F=Gm 9. mgh=mv² 10.qV = mu² 80 12. Suppose that the height in meters of a thrown ball after t seconds is given by h =6+4t-t². Complete the square to find the highest point and the time when this happens. 13. Solve by completing the square c₁t² + cat + 3 = 0. 14. Solve for the time t in the following expression = 0 + vot+at²arrow_forward
- A blacksmith cools a 1.60 kg chunk of iron, initially at a temperature of 650.0° C, by trickling 30.0°C water over it. All the water boils away, and the iron ends up at a temperature of 120.0° C. For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Changes in both temperature and phase. Part A How much water did the blacksmith trickle over the iron? Express your answer with the appropriate units. HÅ mwater = Value 0 ? Units Submit Request Answerarrow_forwardSteel train rails are laid in 13.0-m-long segments placed end to end. The rails are laid on a winter day when their temperature is -6.0° C. Part A How much space must be left between adjacent rails if they are just to touch on a summer day when their temperature is 32.0°C? Express your answer with the appropriate units. ☐ о μΑ ? D = Value Units Submit Previous Answers Request Answer × Incorrect; Try Again; 3 attempts remaining Al Study Tools Looking for some guidance? Let's work through a few related practice questions before you go back to the real thing. This won't impact your score, so stop at anytime and ask for clarification whenever you need it. Ready to give it a try? Start Part B If the rails are originally laid in contact, what is the stress in them on a summer day when their temperature is 32.0°C? Express your answer in pascals. Enter positive value if the stress is tensile and negative value if the stress is compressive. F A Ο ΑΣΦ ? Раarrow_forwardhelp me with this and the step I am so confused. It should look something like the figure i shownarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





