
Interpretation:
Equivalence volume and
Concept Introduction:
Dilution formula is given as follows:
Here,
Explanation of Solution
Dilution formula is given as follows:
Substitute
Rearrange equation (2) to calculate value of
Thus, equivalence volume is
Formula to calculate
Substitute 6.993 for
Formula to calculate
Substitute 7.007 for
Equilibrium for titration reaction is given as follows:
Corresponding expression of
When no acid is added, ICE table is drawn as follows:
Substitute
Simplify to obtain the value of
Formula to calculate
Substitute
Formula to calculate
Substitute 4.15 for
When volume added is
Substitute 7 for
When volume added is
Substitute 7 for
When volume added is
Substitute 7 for
When volume added is
Substitute 7 for
When volume added is
Thus excess
Corresponding ICE table is as follows:
Corresponding expression of
Substitute
Simplify to obtain the value of
Formula to calculate
Substitute
When volume added is
Substitute
When volume added is
Substitute
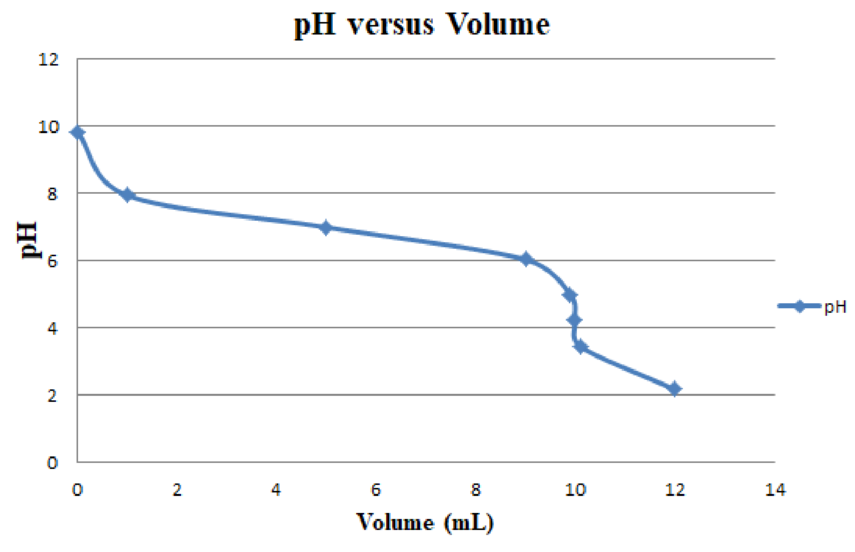
Corresponding plot of
Want to see more full solutions like this?
Chapter 10 Solutions
Exploring Chemical Analysis
- Curved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electron-pushing arrows for the following reaction or mechanistic step(s). Be sure to account for all bond-breaking and bond-making steps. Drawing Arrows THE Problem 33 of 35 N. C:0 Na + Submit Drag To Pan +arrow_forwardDraw the product of the E2 reaction shown below. Include the correct stereochemistry. Ignore and inorganic byproducts.arrow_forwardDraw the major producrs of this SN1 reaction. Ignore any inorganic byproducts. Use a dash or wedge bond to indicate the sereochemistry of substituents on asymmetric centers where appllicable.arrow_forward
- 5) Oxaloacetic Acid is an important intermediate in the biosynthesis of citric acid. Synthesize oxaloacetic acid using a mixed Claisen Condensation reaction with two different esters and a sodium ethoxide base. Give your answer as a scheme Hint 1: Your final acid product is producing using a decarboxylation reaction. Hint 2: Look up the structure of oxalic acid. HO all OH oxaloacetic acidarrow_forward20. The Brusselator. This hypothetical system was first proposed by a group work- ing in Brussels [see Prigogine and Lefever (1968)] in connection with spatially nonuniform chemical patterns. Because certain steps involve trimolecular reac tions, it is not a model of any real chemical system but rather a prototype that has been studied extensively. The reaction steps are A-X. B+X-Y+D. 2X+ Y-3X, X-E. 305 It is assumed that concentrations of A, B, D, and E are kept artificially con stant so that only X and Y vary with time. (a) Show that if all rate constants are chosen appropriately, the equations de scribing a Brusselator are: dt A-(B+ 1)x + x²y, dy =Bx-x²y. diarrow_forwardProblem 3. Provide a mechanism for the following transformation: H₂SO A Me. Me Me Me Mearrow_forward
- You are trying to decide if there is a single reagent you can add that will make the following synthesis possible without any other major side products: xi 1. ☑ 2. H₂O хе i Draw the missing reagent X you think will make this synthesis work in the drawing area below. If there is no reagent that will make your desired product in good yield or without complications, just check the box under the drawing area and leave it blank. Click and drag to start drawing a structure. There is no reagent that will make this synthesis work without complications. : ☐ S ☐arrow_forwardPredict the major products of this organic reaction: H OH 1. LiAlH4 2. H₂O ? Note: be sure you use dash and wedge bonds when necessary, for example to distinguish between major products with different stereochemistry. Click and drag to start drawing a structure. G C टेarrow_forwardFor each reaction below, decide if the first stable organic product that forms in solution will create a new C-C bond, and check the appropriate box. Next, for each reaction to which you answered "Yes" to in the table, draw this product in the drawing area below. Note for advanced students: for this problem, don't worry if you think this product will continue to react under the current conditions - just focus on the first stable product you expect to form in solution. NH2 CI MgCl ? Will the first product that forms in this reaction create a new CC bond? Yes No MgBr ? Will the first product that forms in this reaction create a new CC bond? Yes No G टेarrow_forward
- For each reaction below, decide if the first stable organic product that forms in solution will create a new CC bond, and check the appropriate box. Next, for each reaction to which you answered "Yes" to in the table, draw this product in the drawing area below. Note for advanced students: for this problem, don't worry if you think this product will continue to react under the current conditions - just focus on the first stable product you expect to form in solution. དྲ。 ✗MgBr ? O CI Will the first product that forms in this reaction create a new C-C bond? Yes No • ? Will the first product that forms in this reaction create a new CC bond? Yes No × : ☐ Xarrow_forwardPredict the major products of this organic reaction: OH NaBH4 H ? CH3OH Note: be sure you use dash and wedge bonds when necessary, for example to distinguish between major products with different stereochemistry. Click and drag to start drawing a structure. ☐ : Sarrow_forwardPredict the major products of this organic reaction: 1. LIAIHA 2. H₂O ? Note: be sure you use dash and wedge bonds when necessary, for example to distinguish between major products with different stereochemistry. Click and drag to start drawing a structure. X : ☐arrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





