
Concept explainers
(a)
Draw the vector sum
(a)
Answer to Problem 38P
The vector sum
Explanation of Solution
The figure 1 shows the vector sum of
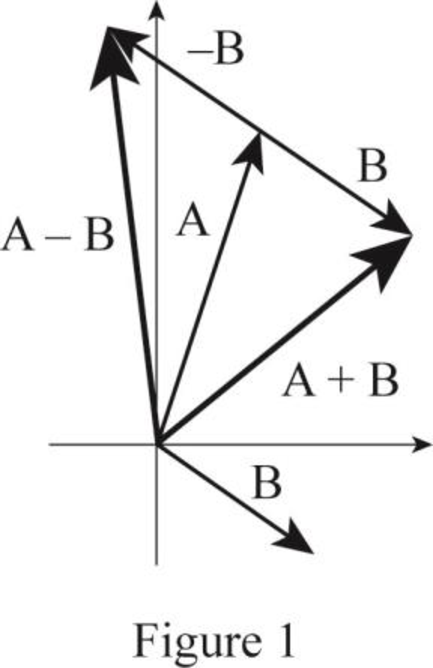
Conclusion:
Therefore, the vector sum
(b)
The components of the unit vectors for
(b)
Answer to Problem 38P
The components of the unit vectors for
Explanation of Solution
Write the expression for the given vector sum
Write the expression for the given vector difference
Conclusion:
Substitute
Substitute
Therefore, the components of the unit vectors for
(c)
The magnitude and direction of the
(c)
Answer to Problem 38P
The magnitude and direction of the
Explanation of Solution
Write the expression for the magnitude of the vector
Here,
Write the expression for the direction of the vector
Write the expression for the magnitude of the vector
Here,
Write the expression for the direction of the vector
Conclusion:
Substitute
Substitute
Substitute
Substitute
Therefore, the magnitude and direction of the
Want to see more full solutions like this?
Chapter 1 Solutions
Principles of Physics: A Calculus-Based Text
- (a) For a spherical capacitor with inner radius a and outer radius b, we have the following for the capacitance. ab C = k₂(b- a) 0.0695 m 0.145 m (8.99 × 10º N · m²/c²)( [0.145 m- 0.0695 m × 10-11 F = PF IIarrow_forwardA pendulum bob A (0.5 kg) is given an initialspeed of vA = 4 m/s when the chord ishorizontal. It then hits a stationary block B (1kg) which then slides to a maximum distanced before it stops. Determine the value of d.The coefficient of static friction between theblock and the plane is μk = 0.2. The coefficientof restitution between A and B is e = 0.8.Ans: d=1.0034 marrow_forwardFigure 29-43 Problem 12. ••13 In Fig. 29-44, point P₁ is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P₁ due to i? P2° R R Larrow_forward
- Checkpoint 1 The figure shows the current i in a single-loop circuit with a battery B and a resistance R (and wires of neg- ligible resistance). (a) Should the emf arrow at B be drawn pointing leftward or rightward? At points a, B C R b, and c, rank (b) the magnitude of the current, (c) the electric potential, and (d) the electric potential energy of the charge carriers, greatest first.arrow_forwardPls help ASAParrow_forwardPls help asaparrow_forward
 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





