
Concept explainers
As depicted in Fig. P1.22, a spherical particle settling through a quiescent luid is subject to three forces: the downward force of gravity
where
(a) Use a force balance for the particle to develop the
(b) At steady-state, use this equation to solve for the particle's terminal velocity.
(c) Employ the result of (b) to compute the particle's terminal velocity in m/s for a spherical silt particle settling in water:
(d) Check whether low is laminar.
(e) Use Euler's method to compute the velocity from
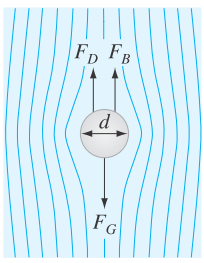
FIGURE P1.22
(a)
The differential equation for
Answer to Problem 22P
Solution:
The differential equation for
Explanation of Solution
Given Information:
The drag force is given as
Where,
The mass of the particle,
The mass of the displaced fluid,
The volume of sphere is
The figure,
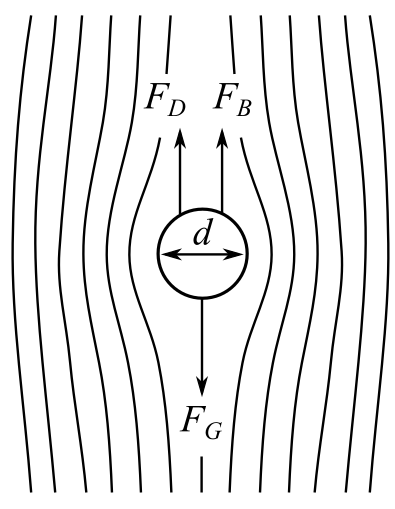
From the provided figure, the drag force and buoyancy force are against the gravitational force.
Therefore, the force balance on the sphere is given as,
Here,
And,
And,
And,
Thus, the force balance on the sphere is,
Divide the both sides of the above equation by m,
Now, the mass of the particle
Substitute
The volume of the sphere is
Substitute
Hence, the differential equation for
(b)
The particle’s terminal velocity at the steady state by the use of the differential equation
Answer to Problem 22P
Solution:
The particle’s terminal velocity at the steady state is
Explanation of Solution
Given Information:
The differential equation
At the steady state, the change in the velocity is zero. Therefore,
Now, solve the above equation for particle’s terminal velocity v as below,
Simplify furthermore,
Hence, the particle’s terminal velocity at the steady state is,
(c)
To calculate: The value of particle’s terminal velocity in m/secif the particle’s terminal velocity is given as
Answer to Problem 22P
Solution:
The value of particle’s terminal velocity in m/sec is
Explanation of Solution
Given Information:
The particle’s terminal velocity is given as
The values,
Formula used:
The conversions,
Calculation:
The particle’s terminal velocity at the steady state is,
Convert the provided values in to the required units as below,
And,
And,
And,
Substitute
Simplify furthermore,
Hence, the value of the particle’s terminal velocity in m/sec is
(d)
Whether the flow is laminar or not if the Reynolds number is given as
Answer to Problem 22P
Solution:
The flow is laminar.
Explanation of Solution
Given Information:
The Reynolds number is given as
The values,
The flow is laminar if the value of Reynolds number is less than 1.
Now, consider the Reynolds number as,
From part (c),
And,
Substitute the values
Since, the Reynolds number is less than 1.
Hence, the flow is laminar.
(e)
To calculate: The velocity from
Answer to Problem 22P
Solution:
The velocity from
| t | v | dv/dt |
| 0 | 0 | 6.10771 |
| 3.8147E-06 | 2.32991E-05 | 3.891969 |
| 7.6294E-06 | 3.81457E-05 | 2.480049 |
| 1.1444E-05 | 4.76064E-05 | 1.580343 |
| 1.5259E-05 | 5.36349E-05 | 1.00703 |
| 1.9073E-05 | 5.74764E-05 | 0.641702 |
| 2.2888E-05 | 5.99243E-05 | 0.408907 |
| 2.6703E-05 | 6.14842E-05 | 0.260564 |
| 3.0518E-05 | 6.24782E-05 | 0.166037 |
Explanation of Solution
Given Information:
The values,
The initial condition
Formula used:
Euler’s method for
Where, h is the step size.
Calculation:
From part (a), the differential equation is,
Convert the provided values in to the standard MKS units as below,
And,
And,
And,
Substitute
The iteration formula for Euler’s method with step size
Use excel to find all the iteration with step size
Step 1: Name the column A as t and go to column A2 and put 0 then go to column A3and write the formula as,
=A2+2^(-18)
Then, Press enter and drag the column up to the
Step 2: Now name the column B as v and go to column B2 and write 0 and then go to the column B3 and write the formula as,
=B3+2^(-18)*(6.10771-95100*B3)
Step 3: Press enter and drag the column up to the
Step 4. Now name the column C as dv/dt and go to column C2 and write the formula as,
=6.10771-95100*B2
Step 5. Press enter and drag the column up to the
Thus, all the iterations are as shown below,
| t | v | dv/dt |
| 0 | 0 | 6.10771 |
| 3.8147E-06 | 2.32991E-05 | 3.891969 |
| 7.6294E-06 | 3.81457E-05 | 2.480049 |
| 1.1444E-05 | 4.76064E-05 | 1.580343 |
| 1.5259E-05 | 5.36349E-05 | 1.00703 |
| 1.9073E-05 | 5.74764E-05 | 0.641702 |
| 2.2888E-05 | 5.99243E-05 | 0.408907 |
| 2.6703E-05 | 6.14842E-05 | 0.260564 |
| 3.0518E-05 | 6.24782E-05 | 0.166037 |
Want to see more full solutions like this?
Chapter 1 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Precalculus: Mathematics for Calculus (Standalone Book)
College Algebra (Collegiate Math)
Thinking Mathematically (6th Edition)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
College Algebra (7th Edition)
Probability And Statistical Inference (10th Edition)
- Golden Ratio search Method f(x) = 2x^3 - 3x^2 - 12x + 1 Golden ratio search rules 1.If f(x) < f(x2): 1. Eliminate all x values less than x2 2. X2 becomes the new a 3. x, becomes the new x2 4. no change in b If f(x) > f(x2): 1. Eliminate all x values greater than x 2. x, becomes the new b 3. x2 becomes the new x 4. no change in aquesion=Narrow the interval in which the minimizer of the function f is located using the golden search method, starting with the initial interval (0,6], until its width is less than 2. Then, accept the midpoint of this interval as an approximate value of the minimizer of the function fand determine it. (ф=0.62)According to the question above, fill in the table below using the algorithm until the appropriate place.please write every step by step in a verry comprehensive wayarrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forwardFor all integers a and b, (a + b)^4 ≡ a^4 + b^4 (mod 4).arrow_forward
- Let Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forwardProve that (1) Σσς (α) μ(η/α) = n d/n (ii) Σσς(d) = η Σσο(α)/d d❘n d❘n (iii) σ (d) σ (n/d) = Σ d³oo(d) σo(n/d). d|n dnarrow_forwardhow to do part b,carrow_forward
- If p = 5 (mod 8), where p is prime, show that p|2 (P-1)/2 + 1. State and prove the corresponding result when p = 7 (mod 8). Deduce that 250 + 1 and 251 1 are composite. -arrow_forwardWhy the character no change for my remark?arrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,



