
Concept explainers
The Wall Street Journal’s website, www.wsj.com, reported the number of cars and light-duty trucks sold by the eight largest automakers in the first 2 months of 2013. Compare the 2013 data to the first 2 months of 2009 as reported below.
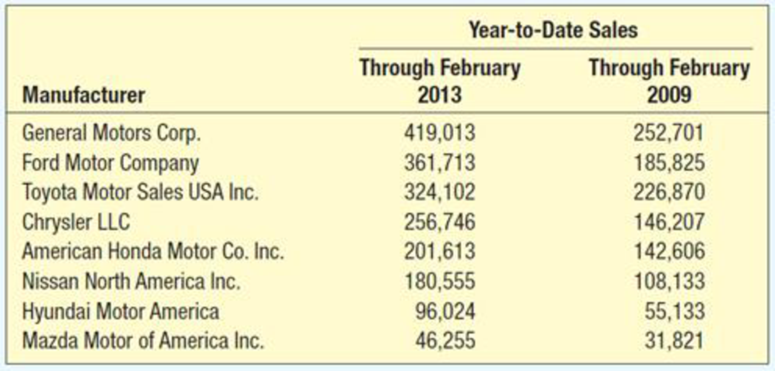
- a. Compare the total sales for the eight automakers. Has there been an increase or a decrease in sales for 2013 compared to the same period in 2009?
- b. The total number of cars and light-duty trucks sold in 2013 was 2.234 million while 1.346 million were sold in 2009. Compute the market share for each of the companies. Has there been a change in the market share for any of the companies?
- c. Compute the percentage change in sales for each of the eight companies. Which companies had a significant change in sales?
a.
Compare the total sales of the given eight automakers.
Check whether there is a change in sales for 2013 when compared to the sales in 2009.
Answer to Problem 17CE
The total sales of the eight automakers increased by 736,725 in 2013 when compared to the year 2009.
Explanation of Solution
The total sales of eight automakers through February 2013 is 18,86,021 and the total sales of eight automakers through February 2009 is 1,149,296.
The difference in total sales of the given eight automakers between 2009 and 2013 is computed as follows:
That is, the total sales in 2013 is increased by 736,725 when compared to the total sales in 2009, which is approximately 64.1%
b.
.
Calculate the market share for each of the companies.
Answer to Problem 17CE
The market share for each of the companies are as follows:
| Manufacturer | Market share in 2013 | Market share in 2009 |
| Company G | 18.76% | 18.77% |
| Company F | 16.19% | 13.81% |
| Company T | 14.51% | 16.86% |
| Company C | 11.49% | 10.86% |
| Company A | 9.02% | 10.59% |
| Company N | 8.08% | 8.03% |
| Company H | 4.30% | 4.10% |
| Company M | 2.07% | 2.36% |
Explanation of Solution
It is given that the total number of cars and light-duty trucks sold in 2013 is 2,234,000 and in 2009 is 1,346,000.
The market share for each of the companies is calculated as follows:
| Manufacturer | Market share in 2013 | Market share in 2009 |
| Company G | ||
| Company F | ||
| Company T | ||
| Company C | ||
| Company A | ||
| Company N | ||
| Company H | ||
| Company M |
Thus, the market share for each company is obtained.
c.
Calculate the percentage change in sales for each of the eight companies.
Identify the company that has a significant change in sales.
Answer to Problem 17CE
The percentage change in sales for each of the eight companies are as follows:
| Manufacturer | Change (%) |
| Company G | 65.81% |
| Company F | 94.65% |
| Company T | 42.86% |
| Company C | 75.60% |
| Company A | 41.38% |
| Company N | 66.97% |
| Company H | 74.17% |
| Company M | 45.36% |
Explanation of Solution
The percentage change in sales for each of the eight companies are calculated as follows:
| Manufacturer | Change (%) |
| Company G | |
| Company F | |
| Company T | |
| Company C | |
| Company A | |
| Company N | |
| Company H | |
| Company M |
It is clear that Company F has the largest percentage change of 94.65%. Whereas, the Companies T, A, and M have the smallest percentage change. These three companies have percentage change of around%.
Want to see more full solutions like this?
Chapter 1 Solutions
Loose Leaf for Statistical Techniques in Business and Economics (Mcgraw-hill/Irwin Series in Operations and Decision Sciences)
- 310015 K Question 9, 5.2.28-T Part 1 of 4 HW Score: 85.96%, 49 of 57 points Points: 1 Save of 6 Based on a poll, among adults who regret getting tattoos, 28% say that they were too young when they got their tattoos. Assume that six adults who regret getting tattoos are randomly selected, and find the indicated probability. Complete parts (a) through (d) below. a. Find the probability that none of the selected adults say that they were too young to get tattoos. 0.0520 (Round to four decimal places as needed.) Clear all Final check Feb 7 12:47 US Oarrow_forwardhow could the bar graph have been organized differently to make it easier to compare opinion changes within political partiesarrow_forwardDraw a picture of a normal distribution with mean 70 and standard deviation 5.arrow_forward
- What do you guess are the standard deviations of the two distributions in the previous example problem?arrow_forwardPlease answer the questionsarrow_forward30. An individual who has automobile insurance from a certain company is randomly selected. Let Y be the num- ber of moving violations for which the individual was cited during the last 3 years. The pmf of Y isy | 1 2 4 8 16p(y) | .05 .10 .35 .40 .10 a.Compute E(Y).b. Suppose an individual with Y violations incurs a surcharge of $100Y^2. Calculate the expected amount of the surcharge.arrow_forward
- 24. An insurance company offers its policyholders a num- ber of different premium payment options. For a ran- domly selected policyholder, let X = the number of months between successive payments. The cdf of X is as follows: F(x)=0.00 : x < 10.30 : 1≤x<30.40 : 3≤ x < 40.45 : 4≤ x <60.60 : 6≤ x < 121.00 : 12≤ x a. What is the pmf of X?b. Using just the cdf, compute P(3≤ X ≤6) and P(4≤ X).arrow_forward59. At a certain gas station, 40% of the customers use regular gas (A1), 35% use plus gas (A2), and 25% use premium (A3). Of those customers using regular gas, only 30% fill their tanks (event B). Of those customers using plus, 60% fill their tanks, whereas of those using premium, 50% fill their tanks.a. What is the probability that the next customer will request plus gas and fill the tank (A2 B)?b. What is the probability that the next customer fills the tank?c. If the next customer fills the tank, what is the probability that regular gas is requested? Plus? Premium?arrow_forward38. Possible values of X, the number of components in a system submitted for repair that must be replaced, are 1, 2, 3, and 4 with corresponding probabilities .15, .35, .35, and .15, respectively. a. Calculate E(X) and then E(5 - X).b. Would the repair facility be better off charging a flat fee of $75 or else the amount $[150/(5 - X)]? [Note: It is not generally true that E(c/Y) = c/E(Y).]arrow_forward
- 74. The proportions of blood phenotypes in the U.S. popula- tion are as follows:A B AB O .40 .11 .04 .45 Assuming that the phenotypes of two randomly selected individuals are independent of one another, what is the probability that both phenotypes are O? What is the probability that the phenotypes of two randomly selected individuals match?arrow_forward53. A certain shop repairs both audio and video compo- nents. Let A denote the event that the next component brought in for repair is an audio component, and let B be the event that the next component is a compact disc player (so the event B is contained in A). Suppose that P(A) = .6 and P(B) = .05. What is P(BA)?arrow_forward26. A certain system can experience three different types of defects. Let A;(i = 1,2,3) denote the event that the sys- tem has a defect of type i. Suppose thatP(A1) = .12 P(A) = .07 P(A) = .05P(A, U A2) = .13P(A, U A3) = .14P(A2 U A3) = .10P(A, A2 A3) = .011Rshelfa. What is the probability that the system does not havea type 1 defect?b. What is the probability that the system has both type 1 and type 2 defects?c. What is the probability that the system has both type 1 and type 2 defects but not a type 3 defect? d. What is the probability that the system has at most two of these defects?arrow_forward
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
 Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning





