Chapter 1, Problem 14CT

(a)

To determine

To find: the zeros of the given function.

Answer to Problem 14CT

The zero is at $x=-5$

Explanation of Solution

Given information:

Consider function $f(x)=|x+5|$

Calculation:

Find the zeros

Find the intercepts:

  $\begin{array}{l}f(x)=|x+5|=0\\ |x+5|=0\\ x+5=0\\ x=-5\end{array}$

Hence, the zero is at $x=-5$

(b)

To determine

To sketch: the graph of the given function using graphing utility.

Explanation of Solution

Given information:

Consider function $f(x)=|x+5|$

Graph:

The graph of the $f(x)=|x+5|$ is shown below.

  

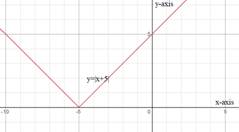
(c)

To determine

To describe: the intervals of increasing and decreasing.

Explanation of Solution

Given information:

Consider function $f(x)=|x+5|$

From part a,

Intervals of increasing $(-\infty ,-5)$

Intervals of decreasing $(-5,\infty )$

(d)

To determine

To find: whether the function is even, odd or neither.

Answer to Problem 14CT

The function is neither even, nor odd.

Explanation of Solution

Given information:

Consider function $f(x)=|x+5|$

Calculation:

  $\begin{array}{l}f(x)=|x+5|\\ f(-x)=|-x+5|\end{array}$

  $\begin{array}{l}f(x)\ne f(-x)\\ f(x)\ne -f(x)\end{array}$

Hence, the function is neither even, nor odd.