
A First Course In Probability, Global Edition
10th Edition
ISBN: 9781292269207
Author: Ross, Sheldon
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1, Problem 1.24P
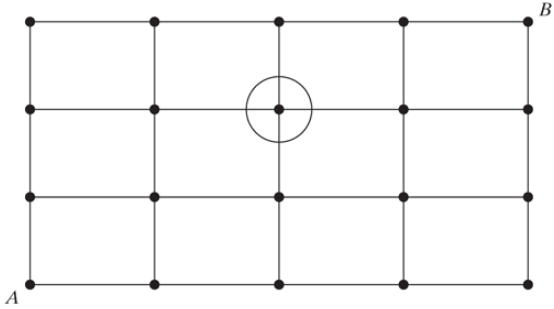
In Problem 23, how many different paths are there from A to B that go through the point circled in the following lattice?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
8.2.5 An article in Obesity Research [“Impaired Pressure
Natriuresis in Obese Youths” (2003, Vol. 11, pp. 745–751)]
described a study in which all meals were provided for 14 lean
boys for three days followed by one stress test (with a video-game
task). The average systolic blood pressure (SBP) during the
test was 118.3 mm HG with a standard deviation of 9.9 mm
HG. Construct a 99% one-sided upper confidence interval for
mean SBP.
8.2.6 An article in Medicine and Science in Sports and
Exercise [“Maximal Leg-Strength Training Improves Cycling
Economy in Previously Untrained Men” (2005, Vol. 37, pp.
131–136)] studied cycling performance before and after 8 weeks
of leg-strength training. Seven previously untrained males performed leg-strength training 3 days per week for 8 weeks (with
four sets of five replications at 85% of one repetition maximum).
Peak power during incremental cycling increased to a mean of
315 watts with a standard deviation of 16 watts. Construct a 95%
confidence…
they take?
8.1.13 WP GO Tutorial An article in the Journal of Agricultural
Science ["The Use of Residual Maximum Likelihood to Model
Grain Quality Characteristics of Wheat with Variety, Climatic
and Nitrogen Fertilizer Effects” (1997, Vol. 128, pp. 135–142)]
investigated means of wheat grain crude protein content (CP) and
Hagberg falling number (HFN) surveyed in the United Kingdom.
The analysis used a variety of nitrogen fertilizer applications (kg
N/ha), temperature (°C), and total monthly rainfall (mm). The
following data below describe temperatures for wheat grown at
Harper Adams Agricultural College between 1982 and 1993. The
temperatures measured in June were obtained as follows:
15.2
14.2
14.0
12.2
14.4
12.5
14.3
14.2
13.5
11.8
15.2
Assume that the standard deviation is known to be σ = 0.5.
a. Construct a 99% two-sided confidence interval on the
mean temperature.
b. Construct a 95% lower-confidence bound on the mean
temperature.
c. Suppose that you wanted to be 95% confident that…
8.1.1 WP For a normal population with known variance σ²,
answer the following questions:
-
a. What is the confidence level for the interval x — 2.140/
√√n≤≤+2.140/√√n?
Chapter 1 Solutions
A First Course In Probability, Global Edition
Ch. 1 - a. How many different 7-place license plates are...Ch. 1 - How many outcome sequences are possible ten a die...Ch. 1 - Twenty workers are to be assigned to 20 different...Ch. 1 - John, Jim, Jay, and Jack have formed a band...Ch. 1 - For years, telephone area codes in the United...Ch. 1 - A well-known nursery rhyme starts as follows: As I...Ch. 1 - a. In how many ways can 3 boys and 3 girls sit in...Ch. 1 - When all letters are used, how many different...Ch. 1 - A child has 12 blocks, of which 6 are black, 4 are...Ch. 1 - In how many ways can 8 people be seated in a row...
Ch. 1 - In how many ways can 3 novels. 2 mathematics...Ch. 1 - How many 3 digit numbers zyz, with x, y, z all...Ch. 1 - How many different letter permutations, of any...Ch. 1 - Five separate awards (best scholarship, best...Ch. 1 - Consider a group of 20 people. If everyone shakes...Ch. 1 - How many 5-card poker hands are there?Ch. 1 - A dance class consists of 22 students, of which 10...Ch. 1 - A student has to sell 2 books from a collection of...Ch. 1 - Seven different gifts are to be distributed among...Ch. 1 - A committee of 7, consisting of 2 Republicans, 2...Ch. 1 - From a group of 8 women and 6 men, a committee...Ch. 1 - A person has 8 friends, of whom S will be invited...Ch. 1 - Consider the grid of points shown at the top of...Ch. 1 - In Problem 23, how many different paths are there...Ch. 1 - A psychology laboratory conducting dream research...Ch. 1 - Show k=0n(nk)2k=3n Simplify k=0n(nk)xkCh. 1 - Expand (3x2+y)5.Ch. 1 - The game of bridge is played by 4 players, each of...Ch. 1 - Expand (x1+2x2+3x3)4.Ch. 1 - If 12 people are to be divided into 3 committees...Ch. 1 - If 8 new teachers are to be divided among 4...Ch. 1 - Ten weight lifters are competing in a team...Ch. 1 - Delegates from 10 countries, including Russia,...Ch. 1 - If 8 identical blackboards are to be divided among...Ch. 1 - An elevator starts at the basement with 8 people...Ch. 1 - We have 520.000 that must be invested among 4...Ch. 1 - Suppose that 10 fish are caught at a lake that...Ch. 1 - Prove the generalized version of the basic...Ch. 1 - Two experiments are to be performed. The first can...Ch. 1 - In how many ways can r objects be selected from a...Ch. 1 - There are (nr) different linear arrangements of n...Ch. 1 - Determine the number of vectors (x1,...,xn), such...Ch. 1 - How many vectors x1,...,xk are there for which...Ch. 1 - Give an analytic proof of Equation (4.1).Ch. 1 - Prove that (n+mr)=(n0)(mr)+(n1)(mr1)+...+(nr)(m0)...Ch. 1 - Use Theoretical Exercise 8 I to prove that...Ch. 1 - From a group of n people, suppose that we want to...Ch. 1 - The following identity is known as Fermats...Ch. 1 - Consider the following combinatorial identity:...Ch. 1 - Show that, for n0 ,i=0n(1)i(ni)=0 Hint: Use the...Ch. 1 - From a set of n people, a committee of size j is...Ch. 1 - Let Hn(n) be the number of vectors x1,...,xk for...Ch. 1 - Consider a tournament of n contestants in which...Ch. 1 - Present a combinatorial explanation of why...Ch. 1 - Argue...Ch. 1 - Prove the multinomial theorem.Ch. 1 - In how many ways can n identical balls be...Ch. 1 - Argue that there are exactly (rk)(n1nr+k)...Ch. 1 - Prob. 1.22TECh. 1 - Determine the number of vectors (xi,...,xn) such...Ch. 1 - How many different linear arrangements are there...Ch. 1 - If 4 Americans, 3 French people, and 3 British...Ch. 1 - A president. treasurer, and secretary. all...Ch. 1 - A student is to answer 7 out of 10 questions in an...Ch. 1 - In how many ways can a man divide 7 gifts among...Ch. 1 - How many different 7-place license plates are...Ch. 1 - Give a combinatorial explanation of the...Ch. 1 - Consider n-digit numbers where each digit is one...Ch. 1 - Consider three classes, each consisting of n...Ch. 1 - How many 5-digit numbers can be formed from the...Ch. 1 - From 10 married couples, we want to select a group...Ch. 1 - A committee of 6 people is to be chosen from a...Ch. 1 - An art collection on auction consisted of 4 Dalis,...Ch. 1 - Prob. 1.14STPECh. 1 - A total of n students are enrolled in a review...Ch. 1 - Prob. 1.16STPECh. 1 - Give an analytic verification of...Ch. 1 - In a certain community, there are 3 families...Ch. 1 - If there are no restrictions on where the digits...Ch. 1 - Verify the...Ch. 1 - Simplify n(n2)+(n3)...+(1)n+1(nn)
Additional Math Textbook Solutions
Find more solutions based on key concepts
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Fill in each blank so that the resulting statement is true.
1. The degree of the polynomial function is _____....
Algebra and Trigonometry (6th Edition)
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...
Introductory Statistics
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
Graphical Approach To College Algebra
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- 8.1.8 A civil engineer is analyzing the compressives trength of concrete. Compressive strength is normally distributed with σ2 = 1000(psi)2. A random sample of 12 specimens has a mean compressive strength ofx = 3250 psi. a. Construct a 95% two-sided confidence interval on mean compressive strength. b. Construct a 99% two-sided confidence interval on mean compressive strength. Compare the width of this confidence interval with the width of the one found in part (a). 8.1.9Suppose that in Exercise 8.1.8 it is desired to estimate the compressive strength with an error that is less than 15 psi at 99% confidence. What sample size is required?arrow_forward8.1.12 Ishikawa et al. [“Evaluation of Adhesiveness of Acinetobacter sp. Tol 5 to Abiotic Surfaces,” Journal of Bioscience and Bioengineering (Vol. 113(6), pp. 719–725)] studied the adhesion of various biofilms to solid surfaces for possible use in environmental technologies. Adhesion assay is conducted by measuring absorbance at A590. Suppose that for the bacterial strain Acinetobacter, five measurements gave readings of 2.69, 5.76, 2.67, 1.62, and 4.12 dyne-cm2. Assume that the standard deviation is known to be 0.66 dyne-cm2. a. Find a 95% confidence interval for the mean adhesion. b. If the scientists want the confidence interval to be no wider than 0.55 dyne-cm2, how many observations should they take?arrow_forwardAnswer questions 8.2.1 and 8.2.2 respectivelyarrow_forward
- 8.2.3 A research engineer for a tire manufacturer is investigating tire life for a new rubber compound and has built 16 tires and tested them to end-of-life in a road test. The sample mean and standard deviation are 60,139.7 and 3645.94 kilometers. Find a 95% confidence interval on mean tire life. 8.2.4 Determine the t-percentile that is required to construct each of the following one-sided confidence intervals: a. Confidence level = 95%, degrees of freedom = 14 b. Confidence level = 99%, degrees of freedom = 19 c. Confidence level = 99.9%, degrees of freedom = 24arrow_forward8.1.6The yield of a chemical process is being studied. From previous experience, yield is known to be normally distributed and σ = 3. The past 5 days of plant operation have resulted in the following percent yields: 91.6, 88.75, 90.8, 89.95, and 91.3. Find a 95% two-sided confidence interval on the true mean yield. 8.1.7 .A manufacturer produces piston rings for an automobile engine. It is known that ring diameter is normally distributed with σ = 0.001 millimeters. A random sample of 15 rings has a mean diameter of x = 74.036 millimeters. a. Construct a 99% two-sided confidence interval on the mean piston ring diameter. b. Construct a 99% lower-confidence bound on the mean piston ring diameter. Compare the lower bound of this confi- dence interval with the one in part (a).arrow_forward8.1.2 .Consider the one-sided confidence interval expressions for a mean of a normal population. a. What value of zα would result in a 90% CI? b. What value of zα would result in a 95% CI? c. What value of zα would result in a 99% CI? 8.1.3 A random sample has been taken from a normal distribution and the following confidence intervals constructed using the same data: (38.02, 61.98) and (39.95, 60.05) a. What is the value of the sample mean? b. One of these intervals is a 95% CI and the other is a 90% CI. Which one is the 95% CI and why?arrow_forward
- 8.1.4 . A confidence interval estimate is desired for the gain in a circuit on a semiconductor device. Assume that gain is normally distributed with standard deviation σ = 20. a. How large must n be if the length of the 95% CI is to be 40? b. How large must n be if the length of the 99% CI is to be 40? 8.1.5 Suppose that n = 100 random samples of water from a freshwater lake were taken and the calcium concentration (milligrams per liter) measured. A 95% CI on the mean calcium concentration is 0.49 g μ g 0.82. a. Would a 99% CI calculated from the same sample data be longer or shorter? b. Consider the following statement: There is a 95% chance that μ is between 0.49 and 0.82. Is this statement correct? Explain your answer. c. Consider the following statement: If n = 100 random samples of water from the lake were taken and the 95% CI on μ computed, and this process were repeated 1000 times, 950 of the CIs would contain the true value of μ. Is this statement correct? Explain your answerarrow_forwardThe Martinezes are planning to refinance their home. The outstanding balance on their original loan is $150,000. Their finance company has offered them two options. (Assume there are no additional finance charges. Round your answers to the nearest cent.) Option A: A fixed-rate mortgage at an interest rate of 4.5%/year compounded monthly, payable over a 30-year period in 360 equal monthly installments.Option B: A fixed-rate mortgage at an interest rate of 4.25%/year compounded monthly, payable over a 12-year period in 144 equal monthly installments. (a) Find the monthly payment required to amortize each of these loans over the life of the loan. option A $ option B $ (b) How much interest would the Martinezes save if they chose the 12-year mortgage instead of the 30-year mortgage?arrow_forwardThe Martinezes are planning to refinance their home. The outstanding balance on their original loan is $150,000. Their finance company has offered them two options. (Assume there are no additional finance charges. Round your answers to the nearest cent.) Option A: A fixed-rate mortgage at an interest rate of 4.5%/year compounded monthly, payable over a 30-year period in 360 equal monthly installments.Option B: A fixed-rate mortgage at an interest rate of 4.25%/year compounded monthly, payable over a 12-year period in 144 equal monthly installments. (a) Find the monthly payment required to amortize each of these loans over the life of the loan. option A $ option B $ (b) How much interest would the Martinezes save if they chose the 12-year mortgage instead of the 30-year mortgage?arrow_forward
- When a tennis player serves, he gets two chances to serve in bounds. If he fails to do so twice, he loses the point. If he attempts to serve an ace, he serves in bounds with probability 3/8.If he serves a lob, he serves in bounds with probability 7/8. If he serves an ace in bounds, he wins the point with probability 2/3. With an in-bounds lob, he wins the point with probability 1/3. If the cost is '+1' for each point lost and '-1' for each point won, the problem is to determine the optimal serving strategy to minimize the (long-run)expected average cost per point. (Hint: Let state 0 denote point over,two serves to go on next point; and let state 1 denote one serve left. (1). Formulate this problem as a Markov decision process by identifying the states and decisions and then finding the Cik. (2). Draw the corresponding state action diagram. (3). List all possible (stationary deterministic) policies. (4). For each policy, find the transition matrix and write an expression for the…arrow_forwardDuring each time period, a potential customer arrives at a restaurant with probability 1/2. If there are already two people at the restaurant (including the one being served), the potential customer leaves the restaurant immediately and never returns. However, if there is one person or less, he enters the restaurant and becomes an actual customer. The manager has two types of service configurations available. At the beginning of each period, a decision must be made on which configuration to use. If she uses her "slow" configuration at a cost of $3 and any customers are present during the period, one customer will be served and leave with probability 3/5. If she uses her "fast" configuration at a cost of $9 and any customers are present during the period, one customer will be served and leave with probability 4/5. The probability of more than one customer arriving or more than one customer being served in a period is zero. A profit of $50 is earned when a customer is served. The manager…arrow_forwardEvery Saturday night a man plays poker at his home with the same group of friends. If he provides refreshments for the group (at an expected cost of $14) on any given Saturday night, the group will begin the following Saturday night in a good mood with probability 7/8 and in a bad mood with probability 1/8. However, if he fail to provide refreshments, the group will begin the following Saturday night in a good mood with probability 1/8 and in a bad mood with probability 7/8 regardless of their mood this Saturday. Furthermore, if the group begins the night in a bad mood and then he fails to provide refreshments, the group will gang up on him so that he incurs expected poker losses of $75. Under other circumstances he averages no gain or loss on his poker play. The man wishes to find the policy regarding when to provide refreshments that will minimize his (long-run) expected average cost per week. (1). Formulate this problem as a Markov decision process by identifying the states and…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY