
(a.)
The graphs of the given parametric equations in the parametric interval
(a.)
Answer to Problem 44E
The graphs of the given parametric equations in the parametric interval
Explanation of Solution
Given:
The parametric equations;
Concept used:
The parametric equations are graphed for each of the given values of
Calculation:
The given parametric equations are
The graphs of these parametric equations in the parametric interval
When
When

When

When

It can be seen that
Conclusion:
The graphs of the given parametric equations in the parametric interval
(b.)
The graphs of the given parametric equations in the parametric interval
(b.)
Answer to Problem 44E
The graphs of the given parametric equations in the parametric interval
Explanation of Solution
Given:
The parametric equations;
Concept used:
The parametric equations are graphed for each of the given values of
Calculation:
The given parametric equations are
The graphs of these parametric equations in the parametric interval
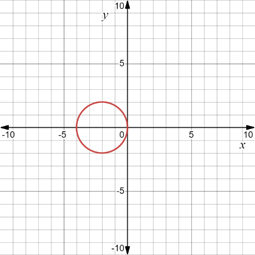
When
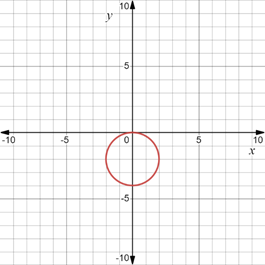
When
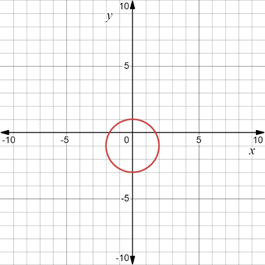
When
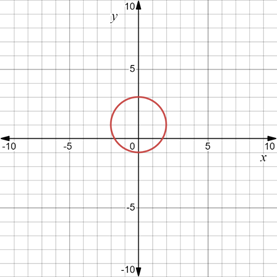
When
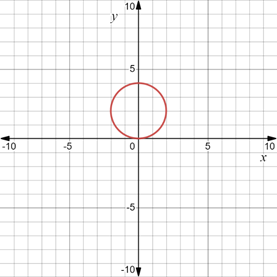
It can be seen that
Conclusion:
The graphs of the given parametric equations in the parametric interval
(c.)
A parametrization of the given circle.
(c.)
Answer to Problem 44E
It has been determined that the parametrization of the given circle is
Explanation of Solution
Given:
The circle with radius
Concept used:
The parametrization;
Calculation:
As seen in the previous parts, the parametrization;
The given circle has radius
Then, here
The center of the given circle is at
Then, here
Put these values in
So, the parametrization of the given circle is
Conclusion:
It has been determined that the parametrization of the given circle is
(d.)
A parameterization for the given ellipse.
(d.)
Answer to Problem 44E
It has been determined that the parameterization for the given ellipse is
Explanation of Solution
Given:
An ellipse centered at
Concept used:
The parametrization of an ellipse centered at
Calculation:
The given ellipse is centered at
Then, here
The length of the semi-major axis of the given ellipse, parallel to the
Then, here
The length of the semi-minor axis of the given ellipse, parallel to the
Then, here
Put these values in
So, the required parametrization is
Conclusion:
It has been determined that the parameterization for the given ellipse is
Chapter 0 Solutions
CALCULUS:GRAPHICAL,...,AP ED.-W/ACCESS
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





