
(a.)
The graphs of the given parametric equations in the parametric interval
(a.)
Answer to Problem 43E
The graphs of the given parametric equations in the parametric interval
Explanation of Solution
Given:
The parametric equations;
Concept used:
The parametric equations are graphed for each of the given values of
Calculation:
The given parametric equations are
The graph of these parametric equations in the parametric interval
are as follows:
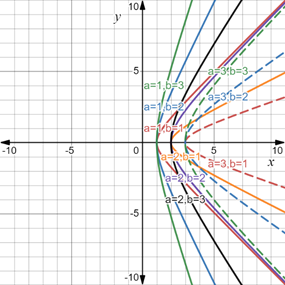
It can be seen that
Conclusion:
The graphs of the given parametric equations in the parametric interval
(b.)
The graph of the given parametric equations in the parametric interval
(b.)
Answer to Problem 43E
The graph of the given parametric equations in the parametric interval
Explanation of Solution
Given:
The parametric equations;
Concept used:
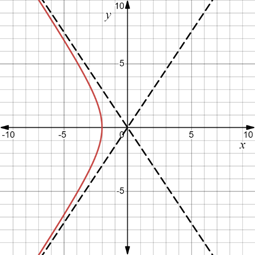
The parametric equations are graphed for the given values of
Calculation:
The given parametric equations are
Put
The graph of these parametric equations in the parametric interval
are as follows:
Conclusion:
The graph of the given parametric equations in the parametric interval
(c.)
The graph of the given parametric equations in the parametric interval
(c.)
Answer to Problem 43E
The graph of the given parametric equations in the parametric interval
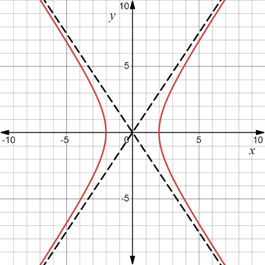
An explanation for the appearance of the lines based on the parameter
Explanation of Solution
Given:
The parametric equations;
Concept used:
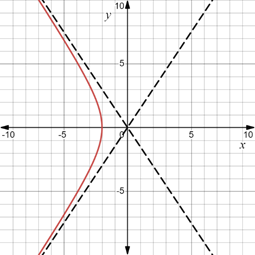
The parametric equations are graphed for the given values of
Calculation:
The given parametric equations are
Put
The graph of these parametric equations in the parametric interval
are as follows:
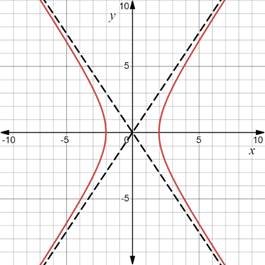
Note that both
So, both
Hence, the graph of these parametric equations is discontinuous at these points.
Since the graph is in connected mode, the dotted lines show up on the graph at these discontinuities.
Conclusion:
The graph of the given parametric equations in the parametric interval
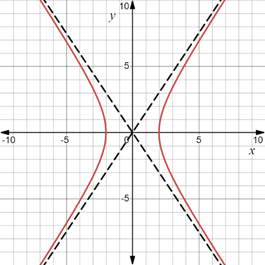
An explanation for the appearance of the lines based on the parameter
(d.)
To Explain:
(d.)
Answer to Problem 43E
It has been explained using algebra why
Explanation of Solution
Given:
The parametric equations;
Concept used:
According to
Calculation:
The given parametric equations are;
Put these values in
Simplifying,
On further simplification,
Put
Simplifying,
This is the required expression.
Conclusion:
It has been explained using algebra why
(e.)
To Repeat: The solutions of part (a), (b) and (d) using an appropriate version of (d) for the given parametric equations.
(e.)
Answer to Problem 43E
The solutions for part (a), (b) and (d) using an appropriate version of (d) have been repeated for the given parametric equations.
Explanation of Solution
Given:
The parametric equations;
Concept used:
The parametric equations are graphed for each of the given values of
Calculation:
The given parametric equations are
The graph of these parametric equations in the parametric interval
are as follows:
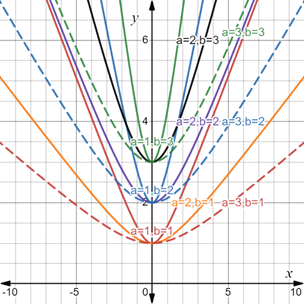
It can be seen that
The graph of the given parametric equations in the parametric interval

Now, for the given parametric equations, it follows that
This can be shown as follows:
Put the given equations;
Simplifying,
On further simplification,
Put
Simplifying,
This is the required proof.
Conclusion:
The solutions for part (a), (b) and (d) using an appropriate version of (d) have been repeated for the given parametric equations.
Chapter 0 Solutions
AP CALCULUS TEST PREP-WORKBOOK
- nd ave a ction and ave an 48. The domain of f y=f'(x) x 1 2 (= x<0 x<0 = f(x) possible. Group Activity In Exercises 49 and 50, do the following. (a) Find the absolute extrema of f and where they occur. (b) Find any points of inflection. (c) Sketch a possible graph of f. 49. f is continuous on [0,3] and satisfies the following. X 0 1 2 3 f 0 2 0 -2 f' 3 0 does not exist -3 f" 0 -1 does not exist 0 ve tes where X 0 < x <1 1< x <2 2arrow_forwardNumerically estimate the value of limx→2+x3−83x−9, rounded correctly to one decimal place. In the provided table below, you must enter your answers rounded exactly to the correct number of decimals, based on the Numerical Conventions for MATH1044 (see lecture notes 1.3 Actions page 3). If there are more rows provided in the table than you need, enter NA for those output values in the table that should not be used. x→2+ x3−83x−9 2.1 2.01 2.001 2.0001 2.00001 2.000001arrow_forwardFind the general solution of the given differential equation. (1+x)dy/dx - xy = x +x2arrow_forwardEstimate the instantaneous rate of change of the function f(x) = 2x² - 3x − 4 at x = -2 using the average rate of change over successively smaller intervals.arrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = 1 to x = 6. Give your answer as a simplified fraction if necessary. For example, if you found that msec = 1, you would enter 1. 3' −2] 3 -5 -6 2 3 4 5 6 7 Ꮖarrow_forwardGiven the graph of f(x) below. Determine the average rate of change of f(x) from x = -2 to x = 2. Give your answer as a simplified fraction if necessary. For example, if you found that msec = , you would enter 3 2 2 3 X 23arrow_forwardA function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forwardUse the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward1. Compute Lo F⚫dr, where and C is defined by F(x, y) = (x² + y)i + (y − x)j r(t) = (12t)i + (1 − 4t + 4t²)j from the point (1, 1) to the origin.arrow_forward2. Consider the vector force: F(x, y, z) = 2xye²i + (x²e² + y)j + (x²ye² — z)k. (A) [80%] Show that F satisfies the conditions for a conservative vector field, and find a potential function (x, y, z) for F. Remark: To find o, you must use the method explained in the lecture. (B) [20%] Use the Fundamental Theorem for Line Integrals to compute the work done by F on an object moves along any path from (0,1,2) to (2, 1, -8).arrow_forwardhelp pleasearrow_forwardIn each of Problems 1 through 4, draw a direction field for the given differential equation. Based on the direction field, determine the behavior of y as t → ∞. If this behavior depends on the initial value of y at t = 0, describe the dependency.1. y′ = 3 − 2yarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





