You wish to test the claim μ<72.7μ<72.7 at a significance level of 0.050.05.You believe the population is normally distributed, but you do not know the standard deviation. You obtain the following sample of data:data39.55749.658.732.349.687.116What is the critical value for this test? (Report answer accurate to three decimal places.)critical value = What is the test statistic for this sample? (Report answer accurate to three decimal places.)test statistic =

Name: You wish to test the claim μ<72.7μ<72.7 at a significance level of 0.0
Uploaded: 2024-03-20T07:07:12.000Z
Channel: Bartleby
Description: You wish to test the claim μ<72.7μ<72.7 at a significance level of 0.050.05.You believe the population is normally distributed, but you do not know the standard deviation. You obtain the following sample of data:data39.55749.658.732.349.687.116What i

Answered: You wish to test the claim μ<72.7μ<72.7…

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Related questions

Topic Video

Question

You wish to test the claim μ<72.7μ<72.7 at a significance level of 0.050.05.

You believe the population is normally distributed, but you do not know the standard deviation. You obtain the following sample of data:

data
39.5
57
49.6
58.7
32.3
49.6
87.1
16

What is the critical value for this test? (Report answer accurate to three decimal places.)
critical value =

What is the test statistic for this sample? (Report answer accurate to three decimal places.)
test statistic =

Features Features Normal distribution is characterized by two parameters, mean (µ) and standard deviation (σ). When graphed, the mean represents the center of the bell curve and the graph is perfectly symmetric about the center. The mean, median, and mode are all equal for a normal distribution. The standard deviation measures the data's spread from the center. The higher the standard deviation, the more the data is spread out and the flatter the bell curve looks. Variance is another commonly used measure of the spread of the distribution and is equal to the square of the standard deviation.

Expert Solution

Step 1

Given Information:

Claim: μ<72.7

Significance level $α = 0.05$

Sample size (n) = 8

Since, the population standard deviation is not known and sample size (n) is less than 30, we use One sample t-test.

State the Hypothesis as follows:

Null Hypothesis: $H_{0} : μ \geq 72.7$

Alternative Hypothesis: $H_{1} : μ < 72.7$

This is a left tailed test.

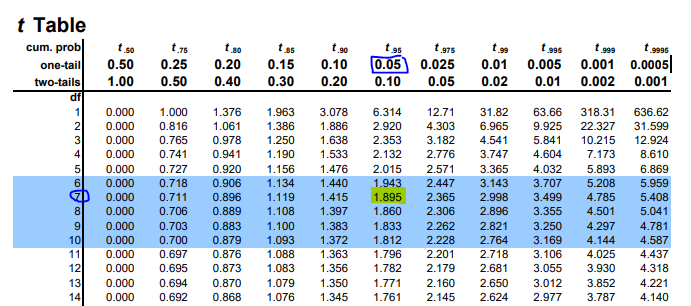
Degrees of freedom $d f = n - 1 = 8 - 1 =$ 7

Using a t-distribution table, critical value at 7 degrees of freedom and 0.05 significance level is -1.895

Step 2

Calculation of the test statistic:

Formula:

$t = \frac{\bar{x} - μ_{0}}{\frac{s}{\sqrt{n}}}$

where, $\bar{x}$ : Sample mean

$μ_{0}$ : Hypothesized value.

$s$ : Sample standard deviation

Sample mean is obtained using the formula:

$\begin{array}{rcl} \bar{x} & = & \frac{\sum_{i} x_{i}}{n} \\ = & \frac{39.5 + 57 + 49.6 + 58.7 + 32.3 + 49.6 + 87.1 + 16}{8} \\ = & \frac{389.8}{8} \\ = & 48.725 \end{array}$

Sample standard deviation is obtained using the formula:

$\begin{array}{rcl} s & = & \sqrt{\frac{\sum_{i} {(x_{i} - \bar{x})}^{2}}{n - 1}} \\ = & \sqrt{\frac{{(39.5 - 48.725)}^{2} + {(57 - 48.725)}^{2} + {(49.6 - 48.725)}^{2} + {(58.7 - 48.725)}^{2} + {(32.3 - 48.725)}^{2} + {(49.6 - 48.725)}^{2} + {(87.1 - 48.725)}^{2} + {(16 - 48.725)}^{2}}{8 - 1}} \\ = & \sqrt{\frac{85.100625 + 68.475625 + 0.765625 + 99.500625 + 269.780625 + 0.765625 + 1472.640625 + 1070.925625}{7}} \\ = & \sqrt{\frac{3067.955}{7}} \\ = & 20.93512087 \\ \approx & 20.94 \end{array}$

Step by step

Solved in 3 steps with 1 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.