You want to see if the percentage of cat owners is significantly different than the percentage of dog owners at a significance level of α=0.05. You sample 223 people and find 110 have cats. You sample an additional 627 people and find 231 have dogs. What is the critical value for this test? (Report answer accurate to three decimal places.) critical value = ±± What is the test statistic for this sample? (Report answer accurate to three decimal places.) test statistic =
You want to see if the percentage of cat owners is significantly different than the percentage of dog owners at a significance level of α=0.05.
You sample 223 people and find 110 have cats. You sample an additional 627 people and find 231 have dogs.
What is the critical value for this test? (Report answer accurate to three decimal places.)
critical value = ±±
What is the test statistic for this sample? (Report answer accurate to three decimal places.)
test statistic =
State the hypotheses.
Let p1 denotes the percentage of cat owners.
Let p2 denotes the percentage of dog owners.
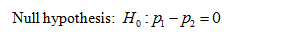
That is, there is no evidence to conclude that percentage of cat owners is significantly different than the percentage of dog owners.
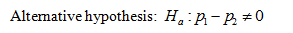
That is, there is evidence to conclude that percentage of cat owners is significantly different than the percentage of dog owners.
Obtain the critical value.
The critical value is obtained below as follows:
Here, confidence level is 0.95.
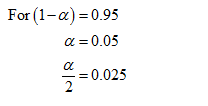
Use EXCEL Procedure for finding the critical value of z in left tail.
Follow the instruction to obtain the critical value of z:
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=NORMINV”
- Enter the probability as 0.025.
- Enter the mean as 0 and the Standard deviation as 1.
- Click enter
EXCEL output:
From the EXCEL output, the critical value of z at the 95% confidence level is –1.960.
Obtain the area of probability in the right tail.
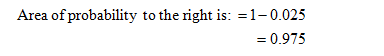
Use EXCEL Procedure for finding the critical value of z.
Follow the instruction to obtain the critical value of z:
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=NORMINV”
- Enter the probability as 0.975
- Enter the mean as 0 and the Standard deviation as 1.
- Click enter
EXCEL output:
From the EXCEL output, the critical value of z at the 95% confidence level is 1.960.
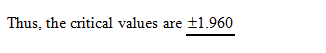
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 9 images




