### Control Systems Problem**Objective:** Find values of $ K_1 $ and $ K_2 $ to yield poles at $ s = -1 \pm j 3 $.**Options:**- (a) $ K_1 = 2, K_2 = 11 $- (b) $ K_1 = 2, K_2 = 9 $- (c) $ K_1 = 9, K_2 = 2 $- (d) $ K_1 = 1, K_2 = 2 $**Question:** When $ K_1 = 6 $ and $ K_2 = 9 $, find the poles of the system.**Calculated Poles:**- (a) $ s_1 = -3, s_2 = -3 $- (b) $ s_1 = -4, s_2 = -3$- (c) $ s_1 = -3 + j 3, s_2 = -3 - j 3 $- (d) $ s_1 = 2.5, s_2 = 4 $**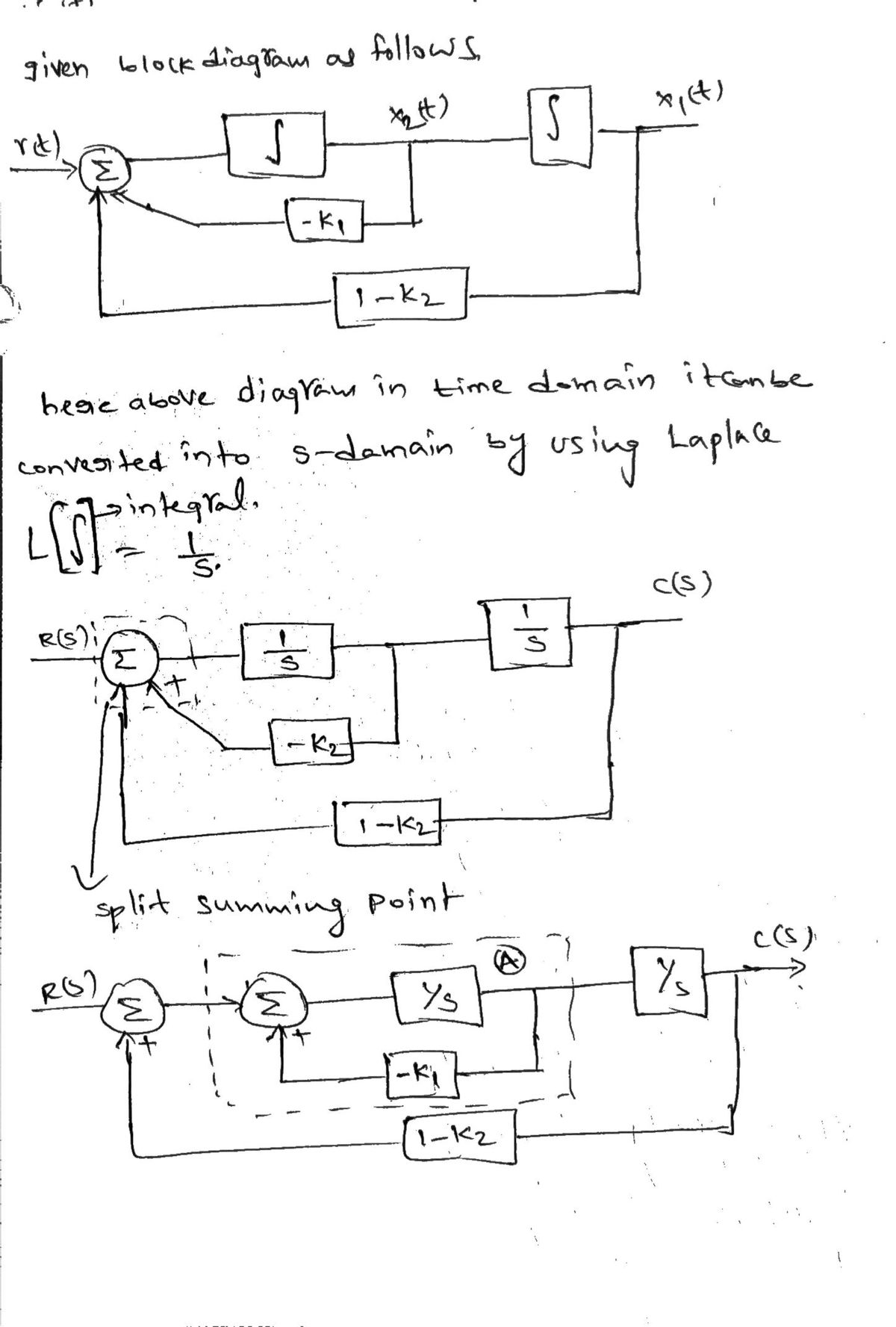Diagram Analysis:**The block diagram represents a control system. The components include:1. **Integrator ($\int$):** Symbolized by a block with an integration sign, indicating the integration of the input signal.2. **Negative Feedback (-K1):** A block representing a multiplication with the constant $-K_1$.3. **Additional Feedback (1-K2):** A block indicating the system output is multiplied by $1-K_2$ before feeding back to the system input.4. **Summing Junction:** Located at the circuit junctions with typical plus and minus signs indicating the addition and subtraction of signals.5. **Signal Path:** The lines connecting each block highlight the flow of control signals through the system.The goal is to manipulate the values $ K_1 $ and $ K_2 $ such that the system provides a desired response characterized by specific pole placements.

Answered: Image /qna-images/answer/186a1d86-222e-4e8e-90af-3587f4c21517.jpg

x₂ (t) AS (a) K₁ = 2, K₂ = 11 (b) K₁ = 2, K₂ = 9 (c) K₁ = 9, K₂ = 2 (d) K₁ = 11, K₂ = 2 -K₂ Find values of K, and K₂ to yield poles at s = -1 ±j3. x, (t) When K₁ = 6 and K₂ = 9, find the poles of the system. (a) S₁ = -3, S₂ = -3 (b) s₁ = -3+j3, S₂ = -3-j3 (c) s₁ = -3+j, $₂ = -3-j (d) $₁ = -2, S₂ = -4

x₂ (t) AS (a) K₁ = 2, K₂ = 11 (b) K₁ = 2, K₂ = 9 (c) K₁ = 9, K₂ = 2 (d) K₁ = 11, K₂ = 2 -K₂ Find values of K, and K₂ to yield poles at s = -1 ±j3. x, (t) When K₁ = 6 and K₂ = 9, find the poles of the system. (a) S₁ = -3, S₂ = -3 (b) s₁ = -3+j3, S₂ = -3-j3 (c) s₁ = -3+j, $₂ = -3-j (d) $₁ = -2, S₂ = -4

Power System Analysis and Design (MindTap Course List)

6th Edition

ISBN:9781305632134

Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma

Publisher:J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma

Chapter6: Power Flows

Section: Chapter Questions

Problem 6.4P

See similar textbooks

Similar questions

Solve using the Gauss-Seidel method. Starting with ?1(0) = 0 = ?2(0) show your solutions for the first 6 iterations.
H.W: Consider the sys. shown below, where the dead time Ta is (0.5) sec. R Ke-Tas s(s2 + 2s + 1) Use Routh's criteria to determine the critical value of (k) for stability of the closed loop sys. and the crossing points on the imaginary axis then find the locations of all roots for the sys. char. eq.
Is the uncontrolled, open loop system? a.unstable b.not asymptotically stable c.asymptotically stable d.unstable
Show all work please!
show steps pls
A rectangular loop carrying current I is placed on the xy-plane. Assume that the corners of the loop are at (0,0),(a,0), (0,b), (a,b). A.) This configuration is used as part of loop detectors installed under pavement at many traffic stop lights. Write a small essay about the function and applications of loop detectors.
1. Duda, problem 2.13. Secion 4.4 13. In many pattern classification problems one has the option either to assign the pattern to one of c classes, or to reject it as being unrecognizable. If the cost for rejects is not too high, rejection may be a desirable action. Let i, j = 1,..., c { i = j i =c+1 otherwise, %3D where , is the loss incurred for choosing the (c + 1)th action, rejection, and is the loss incurred for making any substitution error. Show that the minimum risk is obtained if we decide wi if P (w,\x) > P(wj|x) for all j and if P(@\x) Z 1- 1,/A,, and reject otherwise. What happens if 2, = 0? What happens if 1, > 1,? %3D
12. What is the vector address of Timer 1?
Create the flow diagram.
Drone Parcel Drone Parcel trajector of Parcel af Rer relese time=0: Take off! time= 8.00s: Perul relesed! from drona A parcel is connected to a flying drone as illustrated above. Note that the coordinate system is given with +y pointed in the upwards direction. Holding the parcel, the drone takes off moving straight up with a velocity of 8.40. m/s. Note that, as usual, y = 0 at the ground. After 8.00 s, the drone accidentally releases the parcel! The parcel is in "freefall" immediately after it is released, as defined in Lecture 7. Assume that the magnitude of the acceleration, g = 9.81 m/s?, and that the drone continues with the same velocity after releasing the parcel. Ignore the effects of air-resistance.
Please write all details and properties. I would much appreciate it a lot. Any property or remark, regardless of how insignificant, please include in the answer. Thank you very much.
2) Sketch the Nyqpoiet plot by hand Sor the following systeon, choosing the contour to be to the right of the singularity the jwn axis Nert , wsing on the Nuquist criterion determine the mge of K z0 for which the sustemn is sca ble. Then, redo the Nuguist plot, this time Choosing the contour to be to the left of the imaryi mary the singularity avris. Again; on Osing Phe Ny quist criterion check the of Kz0 for which the sustem is range stable. Are the conswers the same? Should then be K G(s) = R Csra)