Why are constraints in nonlinear programming unnecessary?
In science, nonlinear programming (NLP) is the way toward taking care of a streamlining issue where a portion of the requirements or the target work are nonlinear. An enhancement issue is one of count of the extrema (maxima, minima or fixed purposes) of a target work over a bunch of obscure genuine factors and restrictive as per the general inclination of an arrangement of uniformities and disparities, aggregately named limitations. It is the sub-field of numerical streamlining that manages issues that are not straight.
Relevance:-
An average non-arched issue is that of upgrading transportation costs by determination from a bunch of transportation strategies, at least one of which show economies of scale, with different network and limit requirements. A model would be oil based commodity transport given a determination or blend of pipeline, rail big hauler, street big hauler, stream canal boat, or beach front tankship. Attributable to monetary cluster size the cost capacities may have discontinuities notwithstanding smooth changes. In exploratory science, some straightforward information investigation, (for example, fitting a range with an amount of pinnacles of known area and shape however obscure size) should be possible with direct strategies, yet by and large these issues, likewise, are nonlinear. Commonly, one has a hypothetical model of the framework under investigation with variable boundaries in it and a model the analysis or examinations, which may likewise have obscure boundaries. One attempts to locate a best fit mathematically. For this situation one regularly needs a proportion of the exactness of the outcome, just as the best fit itself.
Definition:-
Let n, m, and p be positive whole numbers. Leave X alone a subset of Rn, let f, gi, and hj be genuine esteemed capacities on X for every I in {1, … , m} and every j in {1, … , p}, with in any event one of f, gi, and hj being nonlinear.
A nonlinear minimization issue is an advancement issue of the structure
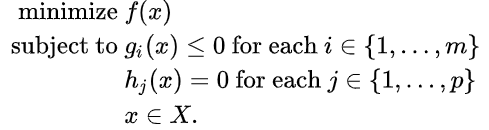
A nonlinear expansion issue is characterized along these lines.
Potential sorts of Constraint set:-
- There are a few opportunities for the idea of the limitation set, otherwise called the achievable set or practical district.
- An infeasible issue is one for which no arrangement of qualities for the decision factors fulfills all the limitations. That is, the limitations are commonly opposing, and no arrangement exists; the achievable set is the vacant set.
- An attainable issue is one for which there exists at any rate one bunch of qualities for the decision factors fulfilling all the imperatives.
- An unbounded issue is an achievable issue for which the target capacity can be made to be superior to some random limited worth. Subsequently there is no ideal arrangement, on the grounds that there is consistently a doable arrangement that gives a superior target work an incentive than does any given proposed arrangement.
Step by step
Solved in 2 steps with 1 images




