We have a free particle in one dimension at a time t 0, the initial wave function is V(x,0) = Ae¯r|æ| %3D where A and r are positive real constants. Calculate the expectation value (p).
Q: A particle of mass m is confined to a harmonic oscillator potential V(X) ! (1/2)kx². The particle…
A: Given, A particle of mass m is confined to harmonic oscillator potential
Q: Suppose you have particle that is trapped in a harmonic potential V=12mω2x2. The particle is in its…
A:
Q: Let ¥₁ (x) and ↳₂2 (x) be normalized stationary states (energy eigenfunctions) of an one-…
A:
Q: Normalize the total wavefunction for a particle in a 2-d box: N sin ("): (") Na,ny (X, y) sin а for…
A:
Q: Calculate the uncertainties dr = V(r2) and dp = Vp?) for a particle confined in the region -a a, r…
A: As we can see the given wave function is normalised and in outside region it's zero. Therefore This…
Q: A particle of mass m, which moves freely inside an infinite potential well of length a, is initially…
A: Given: ψ(x,0)=35asin3πxa+15a sin5πxa For the wavefunction at a later time t we have;…
Q: The displacement x of a classical harmonic oscillator as a function of time is given by x= A…
A: The probability ω(ϕ)dϕ that ϕ lies in the range between ϕ & ϕ+dϕ is then simplyω(ϕ)dϕ=(2π)-1dϕWe…
Q: Question: Particles with energy Ea.
A: Given: The potential in the region is given by: Vx=0 x≤0V0 0<x<a0…
Q: A particle with mass m is moving along the x-axis in a potential given by the potential energy…
A: The potential energy function U(x)=0.5mω2x2 describes a simple harmonic oscillator in quantum…
Q: 0?
A:
Q: We have a free particle in one dimension at a time t = 0, the initial wave function is V (x,0) = Ae…
A:
Q: We have a free particle in one dimension at a time t = 0, the initial wave function is V (x, 0) =…
A: To answer the question, we first write the Normalization condition for a wave function, and then use…
Q: A particle with the energy E is incident from the left on a potential step of height Uo and a…
A: This problem is a combination of step and delta function. There are two regions here, one is x<0,…
Q: Evaluate the following expectation values: (a) ⟨ℓ,m1∣Lx∣ℓ,m2⟩ (b) ⟨ℓ,m1∣Ly∣ℓ,m2⟩
A:
Q: Consider a particle with 1-D wave-function (x) = kexp(-x²). Sketch (x),
A:
Q: What are the expectation values of momentum (p) and p² of a particle in a 1-D box (infinitely hard…
A:
Q: We have a free particle in one dimension at a time t = 0, the initial wave function is ¥ (x,0) =…
A: To find the answer, we first write the expression for expectation value of "x" and substitute the…
Q: Show that is a solution to the time-independent Schrödinger equation, with potential V(x) = 2h²² and…
A: Given: The potential of the particle is Vx = 2 ħ2 m x2 The energy Eigenvalue of the particle is E =…
Q: An electron with initial kinetic energy 6.0 eV encounters a barrier with height 11.0 eV. What is the…
A: Given : Initial kinetic energy of electron = 6.0 eV barrier height = 11.0 eV To find :…
Q: Consider a particle of mass m moving in one dimension with wavefunction $(x) Vi for sin L - and zero…
A: The momentum operator is given by Therefore the operator is given by Where The given wave…
Q: Let y, (x) denote the orthonormal stationary states of a system corresponding to the energy En.…
A: Expectation value of energy
Q: Evaluate , , △x, △px, and △x△px for the provided normalized wave function
A:
Q: The particle is confined to a one-dimensional box between x=0 and x=2. Its wave function is…
A: In an one Dimensional box wave function outside the box is zero as potential is infinite outside the…

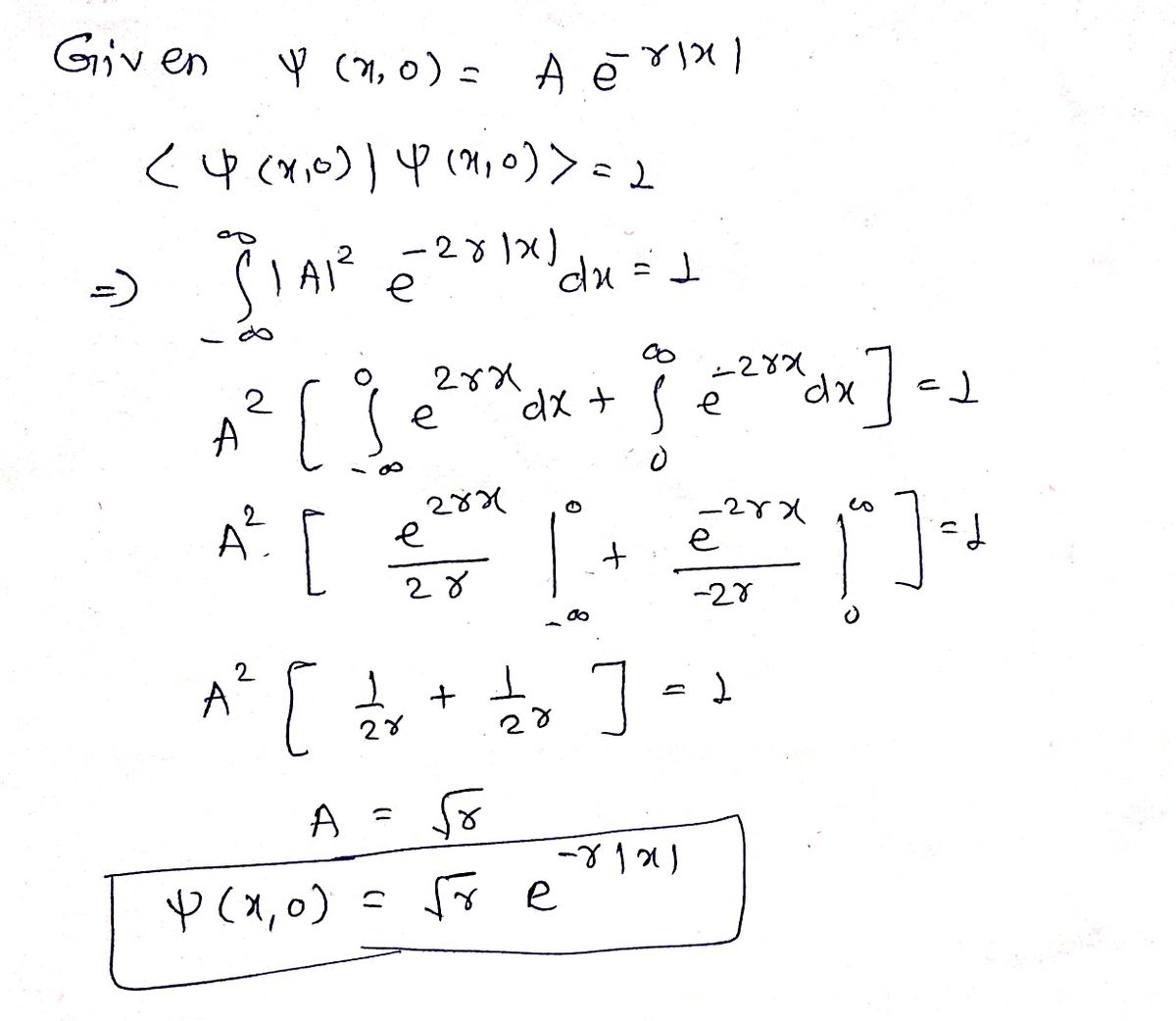
Step by step
Solved in 2 steps with 2 images

- Suppose we had a classical particle in a frictionless box, bouncing back and forth at constant speed. The probability density of the position of the particle in soma box of length L is given by: 0 ans-fawr (7) p(x)= 0 x L a. Sketch the probability density as a function of position b. What must A be in order for p(x) to be normalized? Remember that you are welcome to use resources to solve integrals such as Wolfram Alpha, a table of integrals etc.Calculate the uncertainties dr = V(x2) and op = V(p²) for %3D a particle confined in the region -a a, r<-a. %3DAt time t = 0 a particle is described by the one-dimensional wave function 1/4 (a,0) = (²ª) e-ikre-ar² where k and a are real positive constants. Verify that the wave function (r, 0) is normalised. Hint: you may find the following standard integral useful: Loze -2² dx = √,
- A particle with mass m is in the state mx +iat 2h V (x, t) = Ae where A and a are positive real constants. Calculate the expectation value of (p).A particle is initially prepared in the state of = [1 = 2, m = −1 >|, a) What's the expectation values if we measured (each on the initial state), ,, and Ĺ_ > b) What's the expectation values of ,, if the state was Î_ instead?A particle with mass m is in the state .2 mx +iat 2h Y(x,t) = Ae where A and a are positive real constants. Calculate the expectation values of (x).
- Consider the wavefunction Y(x) = exp(-2a|x|). a) Normalize the above wavefunction. b) Sketch the probability density of the above wavefunction. c) What is the probability of finding the particle in the range 0 < x s 1/a ?Consider the one-dimensional step-potential V (x) = {0 , x < 0; V0 , x > 0}(a) Calculate the probability R that an incoming particle propagating from the x < 0 region to the right will reflect from the step.(b) Calculate the probability T that the particle will be transmitted across the step.(c) Discuss the dependence of R and T on the energy E of the particle, and show that always R+T = 1.[Hints: Use the expression J = (-i*hbar / 2m)*(ψ*(x)ψ′(x) − ψ*'(x)ψ(x)) for the particle current to define current carried by the incoming wave Ji, reflected wave Jr, and transmitted wave Jt across the step.For a simple plane wave ψ(x) = eikx, the current J = hbar*k/m = p/m = v equals the classical particle velocity v. The reflection probability is R = |Jr/Ji|, and the transmission probability is T = |Jt/Ji|. You need to write and solve the Schrodinger equation in regions x < 0 and x > 0 separately, and connect the solutions via boundary conditions at x = 0 (ψ(x) and ψ′(x) must be…Determine the expectation values of the position (x) (p) and the momentum 4 ħ (x)= cos cot,(p): 5V2mw 4 mah 5V 2 sin cot 2 ħ moon (x)= sin cot, (p)= COS at 52mo 2 4 h 4 moh (x)= 52mo sin cot.(p) COS 2 h s cot, (p) 5V2mco 2 moh 5V 2 sin of as a function of time for a harmonic oscillator with its initial state ())))