Use the file on Blackboard called "Excel Databases.xlsx". Locate the Consumer Food tab. Test to determine if there is a significant difference between households in a metro area and households outside the metro area in annual food spending. Assuming a 1% level of significance, use Excel to perform the appropriate two-sample t-test based on the results from the F-test for Equality of Variances. From the t-test, what conclusion can be drawn for this research study? a. There is a significant difference in annual food spending between households in a metro area and outside a metro area. Ob. Households in the metro area spend significantly less on annual food spending than households outside the metro area. Oc. There is not a significant difference in annual food spending between households in a metro area and outside a metro area. Od. Households in a metro area have less variability on annual food spending them households outside the metro area.
| Annual Food Spending ($) | Annual Household Income ($) | Non mortgage household debt ($) | Region: 1 = NE 2 = MW 3 = S 4 = W | Location: 1 = Metro 2 = Outside Metro |
| 8909 | 56697 | 23180 | 1 | 1 |
| 5684 | 35945 | 7052 | 1 | 1 |
| 10706 | 52687 | 16149 | 1 | 1 |
| 14112 | 74041 | 21839 | 1 | 1 |
| 13855 | 63182 | 18866 | 1 | 1 |
| 15619 | 79064 | 21899 | 1 | 1 |
| 2694 | 25981 | 8774 | 1 | 1 |
| 9127 | 57424 | 15766 | 1 | 1 |
| 13514 | 72045 | 27685 | 1 | 1 |
| 6314 | 38046 | 8545 | 1 | 1 |
| 7622 | 52408 | 28057 | 1 | 1 |
| 4322 | 41405 | 6998 | 1 | 1 |
| 3805 | 29684 | 4806 | 1 | 1 |
| 6674 | 49246 | 13592 | 1 | 1 |
| 7347 | 41491 | 4088 | 1 | 1 |
| 2911 | 26703 | 15876 | 1 | 1 |
| 8026 | 48753 | 16714 | 1 | 1 |
| 8567 | 55555 | 16783 | 1 | 1 |
| 10345 | 71483 | 21407 | 1 | 1 |
| 8694 | 50980 | 19114 | 1 | 1 |
| 8821 | 46403 | 7817 | 1 | 1 |
| 8678 | 51927 | 14415 | 1 | 1 |
| 14331 | 84769 | 17295 | 1 | 1 |
| 9619 | 59062 | 16687 | 1 | 1 |
| 9286 | 57952 | 14161 | 1 | 1 |
| 8206 | 58355 | 19538 | 1 | 1 |
| 16408 | 81694 | 15187 | 1 | 1 |
| 12757 | 69522 | 14651 | 1 | 1 |
| 17740 | 96132 | 0 | 1 | 1 |
| 7739 | 57796 | 22057 | 1 | 1 |
| 15383 | 88276 | 1896 | 1 | 1 |
| 4579 | 32264 | 7979 | 1 | 1 |
| 11679 | 65928 | 0 | 1 | 1 |
| 12877 | 69924 | 27330 | 1 | 1 |
| 16232 | 91108 | 9876 | 1 | 1 |
| 9621 | 54070 | 19908 | 1 | 1 |
| 8171 | 47238 | 17819 | 1 | 1 |
| 12128 | 77427 | 31340 | 1 | 1 |
| 8642 | 59805 | 4963 | 1 | 1 |
| 12400 | 60334 | 6632 | 1 | 1 |
| 9185 | 54114 | 18593 | 1 | 2 |
| 7862 | 40680 | 15202 | 1 | 2 |
| 9775 | 58263 | 1486 | 1 | 2 |
| 6771 | 52008 | 21713 | 1 | 2 |
| 3059 | 39643 | 12179 | 1 | 2 |
| 13211 | 70309 | 13221 | 1 | 2 |
| 7408 | 46450 | 5602 | 1 | 2 |
| 11581 | 76140 | 33874 | 1 | 2 |
| 14233 | 80833 | 11478 | 1 | 2 |
| 3352 | 31899 | 2762 | 1 | 2 |
| 2630 | 21647 | 2663 | 1 | 2 |
| 9093 | 65924 | 11355 | 1 | 2 |
| 12652 | 65923 | 5132 | 1 | 2 |
| 9559 | 62811 | 12613 | 1 | 2 |
| 6112 | 42335 | 3149 | 1 | 2 |
| 10431 | 65134 | 15196 | 1 | 2 |
| 12630 | 64621 | 21433 | 1 | 2 |
| 4578 | 36553 | 5502 | 1 | 2 |
| 9551 | 62910 | 11376 | 1 | 2 |
| 10262 | 70727 | 13287 | 1 | 2 |
| 9551 | 57634 | 11857 | 2 | 1 |
| 10143 | 56549 | 16136 | 2 | 1 |
| 8955 | 59662 | 11627 | 2 | 1 |
| 10197 | 57350 | 18432 | 2 | 1 |
| 11234 | 56447 | 10871 | 2 | 1 |
| 9320 | 61136 | 0 | 2 | 1 |
| 9089 | 51526 | 4902 | 2 | 1 |
| 12300 | 79979 | 17270 | 2 | 1 |
| 11484 | 66733 | 15145 | 2 | 1 |
| 11215 | 75359 | 15611 | 2 | 1 |
| 7204 | 40795 | 8975 | 2 | 1 |
| 5579 | 39128 | 6576 | 2 | 1 |
| 11723 | 75482 | 12508 | 2 | 1 |
| 9353 | 63998 | 0 | 2 | 1 |
| 7761 | 45845 | 6671 | 2 | 1 |
| 4261 | 38223 | 8576 | 2 | 1 |
| 9830 | 66787 | 1178 | 2 | 1 |
| 12386 | 77852 | 936 | 2 | 1 |
| 8673 | 55825 | 14167 | 2 | 1 |
| 10944 | 57022 | 9018 | 2 | 1 |
| 9910 | 64263 | 12768 | 2 | 1 |
| 9928 | 75881 | 17423 | 2 | 1 |
| 4264 | 34343 | 21323 | 2 | 1 |
| 7971 | 41243 | 21009 | 2 | 1 |
| 8290 | 53021 | 20151 | 2 | 1 |
| 12669 | 66991 | 9250 | 2 | 1 |
| 7272 | 49719 | 20838 | 2 | 1 |
| 9784 | 58399 | 16065 | 2 | 1 |
| 9187 | 50477 | 9407 | 2 | 1 |
| 5866 | 39112 | 20409 | 2 | 1 |
| 9456 | 51886 | 11668 | 2 | 2 |
| 6270 | 34797 | 146 | 2 | 2 |
| 9518 | 62348 | 5201 | 2 | 2 |
| 10968 | 78704 | 17002 | 2 | 2 |
| 8865 | 53620 | 32004 | 2 | 2 |
| 9226 | 51577 | 15922 | 2 | 2 |
| 4913 | 34761 | 17704 | 2 | 2 |
| 6976 | 60968 | 17799 | 2 | 2 |
| 8152 | 51281 | 8167 | 2 | 2 |
| 2887 | 25013 | 18763 | 2 | 2 |
| 8062 | 59238 | 10815 | 2 | 2 |
| 8895 | 47344 | 11814 | 2 | 2 |
| 8444 | 52645 | 22469 | 2 | 2 |
| 6148 | 35309 | 17139 | 2 | 2 |
| 4563 | 34355 | 10612 | 2 | 2 |
| 8185 | 50630 | 21187 | 3 | 1 |
| 3391 | 29056 | 15735 | 3 | 1 |
| 7436 | 48721 | 18363 | 3 | 1 |
| 9522 | 50459 | 16478 | 3 | 1 |
| 11290 | 72805 | 21238 | 3 | 1 |
| 10403 | 56954 | 22218 | 3 | 1 |
| 4693 | 39343 | 24696 | 3 | 1 |
| 5626 | 38833 | 14371 | 3 | 1 |
| 11869 | 55021 | 35576 | 3 | 1 |
| 13055 | 77605 | 817 | 3 | 1 |
| 8783 | 57937 | 18591 | 3 | 1 |
| 13031 | 63343 | 25531 | 3 | 1 |
| 3681 | 36479 | 17950 | 3 | 1 |
| 5549 | 40381 | 14257 | 3 | 1 |
| 4108 | 26309 | 26581 | 3 | 1 |
| 6314 | 41421 | 22470 | 3 | 1 |
| 7700 | 54579 | 29065 | 3 | 1 |
| 7479 | 40551 | 31757 | 3 | 1 |
| 9093 | 50369 | 6404 | 3 | 1 |
| 9863 | 54422 | 24334 | 3 | 1 |
| 8043 | 51836 | 26213 | 3 | 2 |
| 9552 | 73600 | 36374 | 3 | 2 |
| 9286 | 51873 | 29631 | 3 | 2 |
| 7987 | 48003 | 17261 | 3 | 2 |
| 3875 | 36519 | 13579 | 3 | 2 |
| 10746 | 75152 | 10659 | 3 | 2 |
| 6888 | 44974 | 23711 | 3 | 2 |
| 5479 | 48923 | 4594 | 3 | 2 |
| 6949 | 43769 | 21221 | 3 | 2 |
| 10650 | 75947 | 33357 | 3 | 2 |
| 5188 | 41423 | 33641 | 3 | 2 |
| 5311 | 40189 | 17791 | 3 | 2 |
| 4691 | 36772 | 5829 | 3 | 2 |
| 8056 | 59690 | 19594 | 3 | 2 |
| 11304 | 53654 | 23066 | 3 | 2 |
| 8112 | 59067 | 240 | 3 | 2 |
| 8696 | 65962 | 0 | 3 | 2 |
| 5869 | 37254 | 10157 | 3 | 2 |
| 3776 | 33568 | 14143 | 3 | 2 |
| 11829 | 56934 | 0 | 3 | 2 |
| 13087 | 88822 | 17565 | 4 | 1 |
| 10986 | 59635 | 27863 | 4 | 1 |
| 5762 | 38407 | 18867 | 4 | 1 |
| 11617 | 78627 | 11894 | 4 | 1 |
| 9895 | 47710 | 22930 | 4 | 1 |
| 16293 | 64443 | 31687 | 4 | 1 |
| 8185 | 58871 | 35424 | 4 | 1 |
| 13972 | 87954 | 11549 | 4 | 1 |
| 11243 | 54778 | 12552 | 4 | 1 |
| 4635 | 39825 | 19494 | 4 | 1 |
| 10063 | 49536 | 12195 | 4 | 1 |
| 8426 | 60102 | 13787 | 4 | 1 |
| 7436 | 49139 | 22356 | 4 | 1 |
| 11747 | 51052 | 4553 | 4 | 1 |
| 15397 | 70500 | 12025 | 4 | 1 |
| 6842 | 54894 | 16217 | 4 | 1 |
| 9678 | 60570 | 4106 | 4 | 1 |
| 12852 | 57625 | 31228 | 4 | 1 |
| 10114 | 56956 | 25907 | 4 | 1 |
| 8496 | 61400 | 1093 | 4 | 1 |
| 6689 | 50532 | 17106 | 4 | 1 |
| 15696 | 72774 | 17793 | 4 | 1 |
| 9841 | 69981 | 21607 | 4 | 1 |
| 12529 | 66891 | 17689 | 4 | 1 |
| 10210 | 67431 | 19995 | 4 | 1 |
| 8868 | 64782 | 14489 | 4 | 1 |
| 6426 | 38987 | 17864 | 4 | 1 |
| 11096 | 64867 | 5839 | 4 | 1 |
| 10086 | 50421 | 8689 | 4 | 1 |
| 2587 | 27076 | 17534 | 4 | 1 |
| 12492 | 51784 | 20284 | 4 | 2 |
| 8456 | 54135 | 22037 | 4 | 2 |
| 6801 | 53291 | 23342 | 4 | 2 |
| 6339 | 49804 | 34943 | 4 | 2 |
| 7802 | 52205 | 28579 | 4 | 2 |
| 9717 | 72841 | 22349 | 4 | 2 |
| 6026 | 46238 | 20165 | 4 | 2 |
| 5618 | 45938 | 10538 | 4 | 2 |
| 10217 | 77716 | 18516 | 4 | 2 |
| 8338 | 59711 | 7980 | 4 | 2 |
| 9048 | 42106 | 19786 | 4 | 2 |
| 4017 | 36462 | 9935 | 4 | 2 |
| 10906 | 53403 | 18177 | 4 | 2 |
| 15148 | 71290 | 6696 | 4 | 2 |
| 8830 | 66759 | 20972 | 4 | 2 |
| 8481 | 57616 | 28767 | 4 | 2 |
| 11358 | 76221 | 1373 | 4 | 2 |
| 10553 | 78202 | 5920 | 4 | 2 |
| 6969 | 55164 | 24795 | 4 | 2 |
| 13219 | 61171 | 21482 | 4 | 2 |
| 3543 | 34093 | 25969 | 4 | 2 |
| 7326 | 50647 | 10750 | 4 | 2 |
| 8458 | 59898 | 22940 | 4 | 2 |
| 11766 | 52884 | 25970 | 4 | 2 |
| 9908 | 73629 | 7112 | 4 | 2 |

Question of the problem : Test to determine if there is significant difference between households in a metro area and households outside the metro area in annual food spending . Assuming a 1% level of significance, use excel to perform the appropriate two sample t test based on the results from the F test for equality of variances .
Null and Alternative Hypotheses
The following null and alternative hypotheses need to be tested:
Ho: =
Ha: ≠
This corresponds to a two-tailed test, for which a t-test for two population means, with two independent samples, with unknown population standard deviations will be used.
To perform a t-Test, execute the following steps.
Step 1 : First, perform an F-Test to determine if the variances of the two populations are equal.
- Click the “Data” tab and then click “Data Analysis.”
- Click “F test two sample for variances” and then click “OK.”
- Click the Variable 1 Range box and then type the location for your first set of data.
- Click the Variable 2 box and then type the location for your second set of data.
- Choose an alpha level. In most cases, an alpha level of 0.01 is given .
- Select a location for your output.
- Click “OK.”
Output :
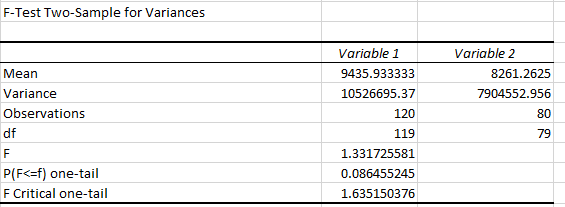
Decision Rule : If your f-value is higher than your F critical value, reject the null hypothesis as your two populations have unequal variances.
The critical value is 1.6351, and since , then the null hypothesis of equal variances is not rejected.
We can conclude that , two variances are equal .
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images









