The reaction C,H, (g) 2C,H,(g) has an activation energy of 262 kJ/mol. At 600.0 K, the rate constant, k, is 6.1 x 10-8s. What is the value of the rate constant at 800.0 K? k = とTOOLS x10
The reaction C,H, (g) 2C,H,(g) has an activation energy of 262 kJ/mol. At 600.0 K, the rate constant, k, is 6.1 x 10-8s. What is the value of the rate constant at 800.0 K? k = とTOOLS x10
Chemistry
10th Edition
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Chapter1: Chemical Foundations
Section: Chapter Questions
Problem 1RQ: Define and explain the differences between the following terms. a. law and theory b. theory and...
Related questions
Question
![**Chemical Kinetics: Calculation of Rate Constant at Different Temperatures**
The following reaction:
\[ \text{C}_4\text{H}_8(\text{g}) \rightarrow 2\text{C}_2\text{H}_4(\text{g}) \]
has an activation energy of 262 kJ/mol. At 600.0 K, the rate constant, \( k \), is \( 6.1 \times 10^{-8} \, \text{s}^{-1} \).
**Question:**
What is the value of the rate constant at 800.0 K?
**Solution:**
This problem can be solved using the Arrhenius equation, which is expressed as:
\[ k = Ae^{-\frac{E_a}{RT}} \]
Where:
- \( k \) is the rate constant,
- \( A \) is the pre-exponential factor,
- \( E_a \) is the activation energy,
- \( R \) is the universal gas constant (8.314 J/mol·K),
- \( T \) is the temperature in Kelvin.
To find the rate constant at a different temperature, you can use the two-point form of the Arrhenius equation:
\[ \ln\left(\frac{k_2}{k_1}\right) = -\frac{E_a}{R}\left(\frac{1}{T_2} - \frac{1}{T_1}\right) \]
Where:
- \( k_1 \) is the rate constant at temperature \( T_1 \),
- \( k_2 \) is the rate constant at temperature \( T_2 \).
Given:
- \( k_1 = 6.1 \times 10^{-8} \, \text{s}^{-1} \) at \( T_1 = 600.0 \, \text{K} \),
- \( T_2 = 800.0 \, \text{K} \),
- \( E_a = 262 \, \text{kJ/mol} = 262000 \, \text{J/mol} \).
You can input these values into the equation to solve for \( k_2 \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F04d91ec5-5dc8-475a-a219-706d13e893d1%2Fa2f65de1-2df4-440f-b583-8f78025ea0a6%2Fpxdy2m.jpeg&w=3840&q=75)
Transcribed Image Text:**Chemical Kinetics: Calculation of Rate Constant at Different Temperatures**
The following reaction:
\[ \text{C}_4\text{H}_8(\text{g}) \rightarrow 2\text{C}_2\text{H}_4(\text{g}) \]
has an activation energy of 262 kJ/mol. At 600.0 K, the rate constant, \( k \), is \( 6.1 \times 10^{-8} \, \text{s}^{-1} \).
**Question:**
What is the value of the rate constant at 800.0 K?
**Solution:**
This problem can be solved using the Arrhenius equation, which is expressed as:
\[ k = Ae^{-\frac{E_a}{RT}} \]
Where:
- \( k \) is the rate constant,
- \( A \) is the pre-exponential factor,
- \( E_a \) is the activation energy,
- \( R \) is the universal gas constant (8.314 J/mol·K),
- \( T \) is the temperature in Kelvin.
To find the rate constant at a different temperature, you can use the two-point form of the Arrhenius equation:
\[ \ln\left(\frac{k_2}{k_1}\right) = -\frac{E_a}{R}\left(\frac{1}{T_2} - \frac{1}{T_1}\right) \]
Where:
- \( k_1 \) is the rate constant at temperature \( T_1 \),
- \( k_2 \) is the rate constant at temperature \( T_2 \).
Given:
- \( k_1 = 6.1 \times 10^{-8} \, \text{s}^{-1} \) at \( T_1 = 600.0 \, \text{K} \),
- \( T_2 = 800.0 \, \text{K} \),
- \( E_a = 262 \, \text{kJ/mol} = 262000 \, \text{J/mol} \).
You can input these values into the equation to solve for \( k_2 \).
Expert Solution
Step 1
Arrhenius equation:
If we know the value of the rate constant at two different temperatures, we can calculate the activation energy by using the Arrhenius equation. The Arrhenius equation is given by:
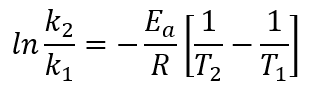
where k2 = rate constant at the T2 temperature
k1 = rate constant at T1 = 6.1 x 10-8 s-1
Ea = activation energy = 262 kJ/mol
R = gas constant = 8.314 J/K.mol
T1 = 600.0 K
T2 = 800.0 K
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Organic Chemistry
Chemistry
ISBN:
9780078021558
Author:
Janice Gorzynski Smith Dr.
Publisher:
McGraw-Hill Education

Chemistry: Principles and Reactions
Chemistry
ISBN:
9781305079373
Author:
William L. Masterton, Cecile N. Hurley
Publisher:
Cengage Learning

Elementary Principles of Chemical Processes, Bind…
Chemistry
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY