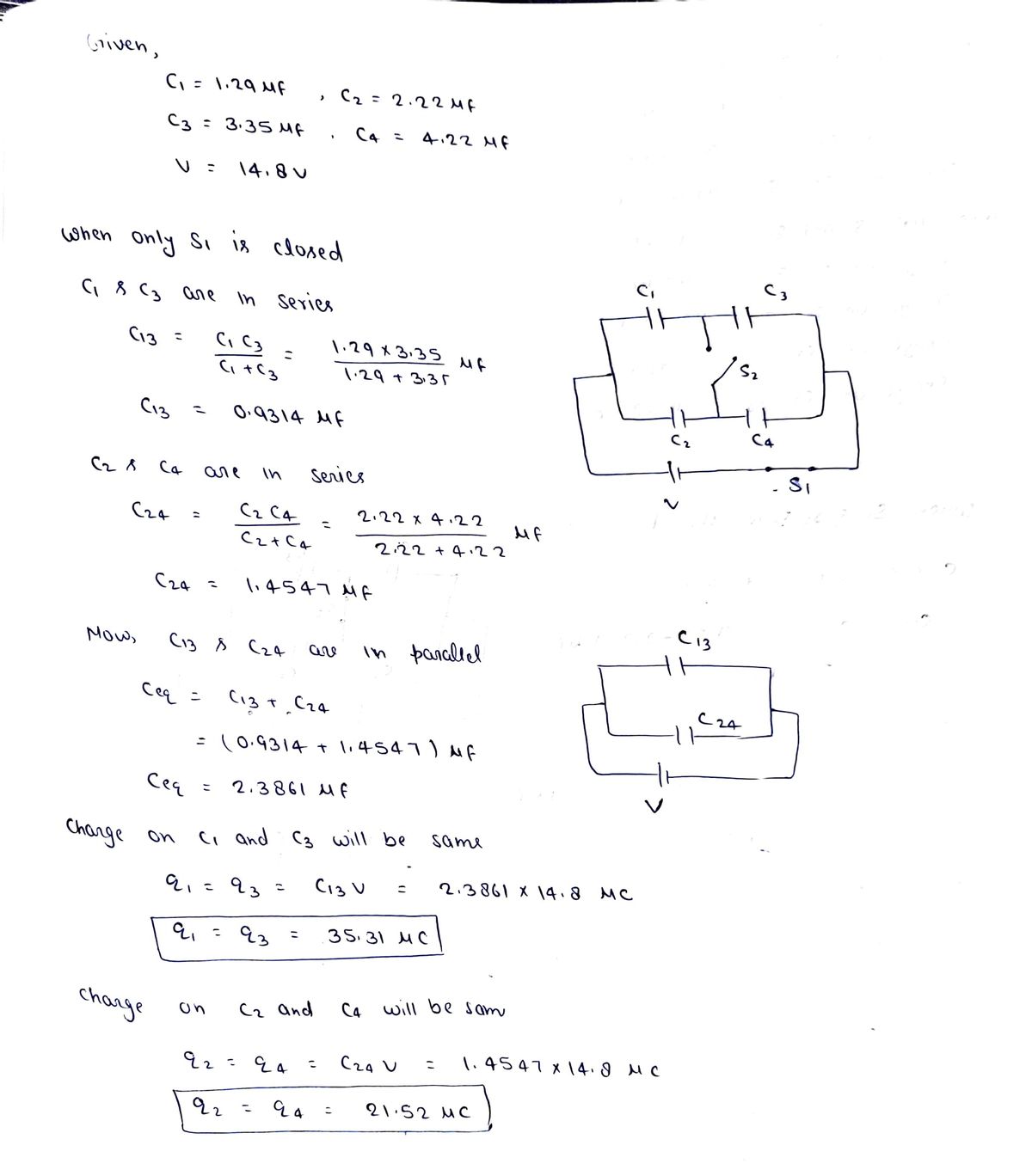
The figure shows a 14.8 V battery and four uncharged capacitors of capacitances C₁ = 1.29 μF,C₂ = 2.22 µF,C3 = 3.35 µF, and C4 = 4.22 µF. If only switch S₁ is closed, what is the charge on (a) capacitor 1, (b) capacitor 2, (c) capacitor 3, and (d) capacitor 4? If both switches are closed, what is the charge on (e) capacitor 1, (f) capacitor 2, (g) capacitor 3, and (h) capacitor 4?
The figure shows a 14.8 V battery and four uncharged capacitors of capacitances C₁ = 1.29 μF,C₂ = 2.22 µF,C3 = 3.35 µF, and C4 = 4.22 µF. If only switch S₁ is closed, what is the charge on (a) capacitor 1, (b) capacitor 2, (c) capacitor 3, and (d) capacitor 4? If both switches are closed, what is the charge on (e) capacitor 1, (f) capacitor 2, (g) capacitor 3, and (h) capacitor 4?
Related questions
Question

Transcribed Image Text:The figure shows a 14.8 V battery and four uncharged capacitors with capacitances \( C_1 = 1.29 \, \mu \text{F}, C_2 = 2.22 \, \mu \text{F}, C_3 = 3.35 \, \mu \text{F}, \) and \( C_4 = 4.22 \, \mu \text{F} \). If only switch \( S_1 \) is closed, what is the charge on:
- (a) capacitor 1,
- (b) capacitor 2,
- (c) capacitor 3, and
- (d) capacitor 4?
If both switches are closed, what is the charge on:
- (e) capacitor 1,
- (f) capacitor 2,
- (g) capacitor 3, and
- (h) capacitor 4?
**Diagram Explanation:**
The circuit diagram depicts a simple electrical network:
- Capacitors \( C_1 \) and \( C_2 \) are in series connected to switch \( S_1 \).
- Capacitors \( C_3 \) and \( C_4 \) are in series connected to switch \( S_2 \).
- The battery \( B \) is positioned at the bottom of the circuit, represented by a standard battery symbol, and it is connected to both the \( S_1 \) and \( S_2 \) switches.
The configuration allows for analysis of different charging scenarios based on which switches are closed.
Expert Solution
Step 1: Charge on capacitors when only S1 is closed
Step by step
Solved in 3 steps with 3 images
