Answered: Suppose that you have the Lagrangian L… | bartleby

Related questions

Question

Suppose that you have the Lagrangian L = 21 (;² + è°r2) +
420
for a 2D
20
system in plane polar coordinates (r, 0).
Determine the pr and pe canonical coordinates.

Expert Solution

Concept

Conjugate momenta P_q corresponding to conjugate variable q is given by

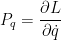
Where L = Lagrangian of the system

Step by step

Solved in 3 steps with 6 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

a2 Laplacian operator 72 = ax? ay? T əz2 in spherical polar coordinates is given by az? p² = () 1 a 1 1 a2 r2 sin e ae sin 0-) is an eigenfunction of the Laplacian operator and find the +- r2 sin 0 a0 r2 ar ar. r2 sin? 0 a20 sin 0 sin o Show that function r2 corresponding eigenvalue.
Problem 4.25 If electron, radius [4.138] 4πεmc2 What would be the velocity of a point on the "equator" in m /s if it were a classical solid sphere with a given angular momentum of (1/2) h? (The classical electron radius, re, is obtained by assuming that the mass of the electron can be attributed to the energy stored in its electric field with the help of Einstein's formula E = mc2). Does this model make sense? (In fact, the experimentally determined radius of the electron is much smaller than re, making this problem worse).
Prove that ||A + B|| ≤ ||A|| + ||B||. This is called the triangle inequality; in twoor three dimensions, it simply says that the length of one side of a triangle ≤sum of the lengths of the other 2 sides. Hint: To prove it in n-dimensional space, write the square of the desired inequality using (10.2) and also use the Schwarz inequality (10.4). Generalize the theorem to complex Euclidean space by using (10.7) and (10.9).
Please obtain the same result as in the book.
O Consider the kinetic energy matrix elements between Hydrogen states (n' = 4, l', m'| |P|²| m -|n = 3, l, m), = for all the allowed l', m', l, m values. What kind of operator is the the kinetic energy (scalar or vector)? Use this to determine the following. For what choices of the four quantum numbers (l', m', l, m) can the matrix elements be nonzero (e.g. (l', m', l, m) (0, 0, 0, 0),...)? Which of these nonzero values can be related to each other (i.e. if you knew one of them, you could predict the other)? In this sense, how many independent nonzero matrix elements are there? (Note: there is no need to calculate any of these matrix elements.)
please solve
Provide a written answer
The operator în · ở measures spin in the direction of unit vector f = (nx, Ny, N₂) nx = sin cosp ny = sinesino nz = cose in spherical polar coordinates, and ở = (x, y, z) for Pauli spin matrices. (a) Determine the two eigenvalues of û.o.
Prove that the function f = (sin kx)(sin my)(sin nz) where: k, m, n are constants is an eigenfunction of the Laplacian operator 2² v² = + 2² 2² 2 2 əx² ay² dz² What are the eigenvalues? +
Prove that adding a constant to the Lagrangian L or else multiplying the Lagrangian by a constant produces a new Lagrangian L′ that is physically equivalent to L. (Physically equivalent means that the Euler-Lagrange equations for the q(t) remain the same under this change of Lagrangian).