Answered: Suppose that k = 170 N/m . (Figure 1)… | bartleby

Related questions

Question

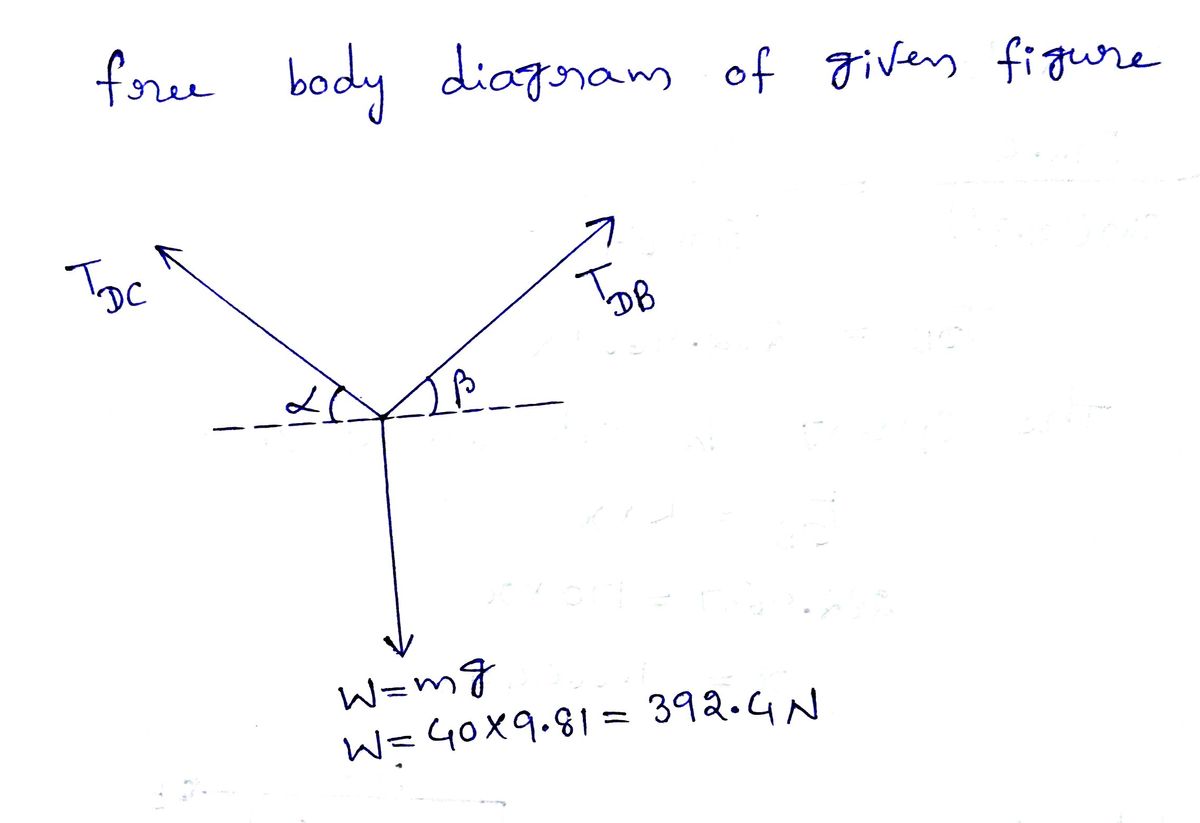
Suppose that k = 170 N/m . (Figure 1)
Part A
Determine the unstretched length of DB to hold the 40-kg crate in the position shown.
Express your answer to three significant figures and include the appropriate units.
HA
?
= 1
Value
Units
Figure
1 of 1
Submit
Request Answer
2 m
-3 m
Provide Feedback
2 m
www
図

Expert Solution

Step 1

Trending now

This is a popular solution!

Step by step

Solved in 4 steps with 4 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

Learning Goal: To understand the use of Hooke's law for a spring. Hooke's law states that the restoring force F on a spring when it has been stretched or compressed is proportional to the displacement of the spring from its equilibrium position. The equilibrium position is the position at which the spring is neither stretched nor compressed. Recall that Fx means that F is equal to a constant times . For a spring, the proportionality constant is called the spring constant and denoted by k. The spring constant is a property of the spring and must be measured experimentally. The larger the value of k, the stiffer the spring. In equation form, Hooke's law can be written F = -kz. The minus sign indicates that the force is in the opposite direction to that of the spring's displacement from its equilibrium length and is "trying" to restore the spring to its equilibrium position. The magnitude of the force is given by F = kx, where is the magnitude of the displacement. In Haiti, public…
In each trial of study 1, the source of kinetic energy of C1 was which of the following? a. The kinetic energy stored in C2 before the spring was released. b. The potential energy stored in C2 before the spring was released. c. The kinetic energy stored in the spring before the spring was released. d. The potential energy stored in the spring before the spring was released.
A wire stretches from 2000 mm to 2005 mm when a 500-N box hangs from one end of it. The wire has a cross sectional area of 0.01 cm2. Calculate the Young's modulus of the wire. a. 5.0 × 1012 N/m2 b. 1.0 × 109 N/m2 c. 2.0 × 1011 N/m2 d. 2.0 × 109 N/m2 e. 1.0 × 1011 N/m2
Part A A 0.300 kg oscillator has a speed of 96.4 cm/s when its displacement is 3.00 cm and 72.4 cm/s when its displacement is 6.50 cm. What is the oscillator's maximum speed? Express your answer with the appropriate units. μΑ Value Units Umax Submit Request Answer Provide Feedback
Learning Goal: To understand the use of Hooke's law for a spring. Hooke's law states that the restoring force F on a spring when it has been stretched or compressed is proportional to the displacement of the spring from its equilibrium position. The equilibrium position is the position at which the spring is neither stretched nor compressed. Recall that Fx I means that F is equal to a constant times 2. For a spring, the proportionality constant is called the spring constant and denoted by k. The spring constant is a property of the spring and must be measured experimentally. The larger the value of k, the stiffer the spring. In equation form, Hooke's law can be written F = -kz. The minus sign indicates that the force is in the opposite direction to that of the spring's displacement from its equilibrium length and is "trying" to restore the spring to its equilibrium position. The magnitude of the force is given by F = kx, where z is the magnitude of the displacement. ▼ A 62 kg driver…
3kg mass is suspended from a spring It oscillates with period=6 seconds when it is pulled 0.1m below equilibrium 1. What is the time taken to move from 0.035 m below equilibrium position to 0.035 m above it when moving upwards 2. What is the total mechanical energy of this motion? 3. The motion of the mass is stopped, and the mass is removed. How much does the spring shorten?
A block with mass 0.50 kg is forced against a horizontal spring of negligible mass, compressing the spring a distance of 0.20 m (Figure 1). When released, the block moves on a horizontal tabletop for 1.00 m before coming to rest. The spring constant k is 100 N/m. Part A What is the coefficient of kinetic friction between the block and the tabletop? Hk = Submit Request Answer Provide Feedback Figure k = 100 N/m m = 0.50 kg 0.20 m 1.00 m
Calculate the work required to stretch the following springs 0.5m from their equilibrium positions. Assume Hooke's law is obeyed. a. A spring that required a force of 40N to be stretched 0.1m from its equilibrium position. b. A spring that required 40J of work to be stretched 0.4m from its equilibrium position.
A spring is hung from a ceiling, and an object attached to its lower end stretches the spring by a distance d = 7.70 cm from its unstretched position when the system is in equilibrium as in the figure below. If the spring constant is 55.0 N/m, determine the mass of the object. kg Need Help? Read It WWwwW
Problem 10.21 - Enhanced - with Expanded Hints The spring in (Figure 1) is compressed by 10 cm. It launches a block across a frictionless surface at 0.50 m/s. The two springs in (Figure 2 ) are identical to the spring of (Figure 1). They are compressed by the same 10 cm and launch the same block. Figure 25 N/m 10 cm 1.0 kg T Xeq 1 of 2 Part A What is the block's speed now? Express your answer with the appropriate units. ► View Available Hint(s) V₂ = 0.35 Submit μA Provide Feedback 1 Previous Answers m S B ? X Incorrect; Try Again; 5 attempts remaining
Learning Goal: To understand the use of Hooke's law for a spring. Hooke's law states that the restoring force F on a spring when it has been stretched or compressed is proportional to the displacement of the spring from its equilibrium position. The equilibrium position is the position at which the spring is neither stretched nor compressed. Recall that Fx means that F is equal to a constant times. For a spring, the proportionality constant is called the spring constant and denoted by k. The spring constant is a property of the spring and must be measured experimentally. The larger the value of k, the stiffer the spring. In equation form, Hooke's law can be written F = -kz. The minus sign indicates that the force is in the opposite direction to that of the spring's displacement from its equilibrium length and is "trying" to restore the spring to its equilibrium position. The magnitude of the force is given by F = kx, where x is the magnitude of the displacement. In Haiti, public…
A spring scale hung from the ceiling stretches by 5.4 cm when a 1.0 kg mass is hung from it. The 1.0 kg mass is removed and replaced with a 1.5 kg mass.

SEE MORE QUESTIONS