Suppose A and B are events in a sample space with P(A) = 0.61, P(B) = 0.66, P(BUA) = 0.93 Find the following probabilities. P(An B) = P(B|A) = P(A/B) =
Q: nd the probabilities for simple events E4 and E5. =4) √5) = = =
A: We are going to find the following probability by the help general formula of probability that sum…
Q: A sample space consists of 9 elementary outcomes E₁, E2, ..., E, whose probabilities are:…
A:
Q: In 2016 Canada was home to 7.54 million foreign-born residents, or 21.9 percent of the population. A…
A: Let X denote the number of residents are foreign-born. Then X follows a Binomial distribution with…
Q: State Farm Insurance studies show that in Colorado, 65% of the auto insurance claims submitted for…
A: Given that n=8 , p=65%=0.65 , q=1-p=1-0.65=0.35 R~Binomial(n=8,p=0.65) r be the number of claims…
Q: the expectation of the sum of points in tossing a pair of fair dice is: - the variance is:
A:
Q: Let E and F be events of a sample space such that P(E)=0.46, P(F)=0.35 and P(EnF)=0.10. Find the…
A: We have to answer question based on conditional probability.
Q: If 30% of the people in a community have internet access from their homes, find the following…
A: also the number of trails of the experiment should be known and also , the probability of success p…
Q: The prior probabilities for two events A1 and A2 are P(A1) = .30 and P(A2) = .70. It is also known…
A: Given P(A1)=0.30, P(A2)=0.70, P(A1 and A2)=0 P(B/A1)=0.15, P(B/A2)=0.05 Note: According to…
Q: An oil company purchased an option on land in Alaska. Preliminary geologic studies assigned the…
A: Given:P(high-quality oil) = 0.55 P(medium-quality oil) = 0.20 P(no oil) = 0.25 a. The probability of…
Q: Suppose A and B are events in a sample space with P(A) = 0.6, P(B) = 0.65, P(BUA) = 0.84 Find the…
A:
Q: Which of the following probabilities are feasible for an experiment having sample space (S₁, S2,…
A:
Q: Suppose that the number of guests per month that members of a country club bring to golf is given by…
A: According to question, Number of guests (x) Probability 0 0.56 1 0.18 2 0.13 3 0.13…
Q: The major airline industry is subject to labor strikes by the pilots, mechanics, and flight…
A: Event A defines strike by the pilots, event B defines the strike by the mechanics and event C…
Q: Suppose that A and B are events defined on a common sample space and that the following…
A: Obtain the probability of P(A or B). The probability of P(A or B) is obtained below as follows:…
Q: The relative frequency table describes whether a group of employees from an accounting firm watch…
A: Events are independent if the outcome of one event does not affect the probability of the other…
Q: Given the soil found in the test, use Bayes' theorem to compute the following revised probabilities…
A:
Q: If X is a random variable that distributes t-students with 12 degrees of freedom, using the table,…
A: X is a random variable with t distribution
Q: ine is causing quality problems as 4% of the engine parts produced on the machine have been found to…
A: Given, the proportion of defective parts produced on the machine (p) = 0.04 sample size(n)=50 Let…
Q: Q1. (a) What is the probability of exactly no heads in tossing a coin two times. (b) Consider the…
A:
Q: Let E and F be two events of an experiment with sample space S. Suppose P(E) = 0.52, P(F) = 0.31,…
A: Compute the probability as follows.
Q: The prior probabilities for events Aj and Az are P(A1) = 0.40 and P(A2) = 0.60. It is also known…
A: As per our guidelines, we are allowed to answer first three sub-parts only. Thanks Mutually…
Q: etermine which of the following probabilities to the three (3) outcomes of an Experiment are valid.…
A:
Q: et A and B be two events in a sample space U, such that: P(A) = 0.55, P(B) = 0.25 and P(AuB) = 0.60…
A: a) The union probability for any two events A and B is defined as P(A ∪ B) = P(A) + P(B) – P(A ∩…
Q: Suppose P(B) = 0.41 P( A )= 0.57 , and P(A and B )= 0.22 . Determine the following probabilities: Do…
A: The question is about probability.Given :P ( B ) = 0.41P ( A ) = 0.57P ( A and B ) = 0.22
Q: (a) What is the probability of shortage of material in any day? Shortage occurs whenever the…
A:
Q: P(E:) = 25, P (E>) = 1 An experiment results in one of five sample points with probabilities P P(E)…
A:
Q: State Farm Insurance studies show that in Colorado, 65% of the auto insurance claims submitted for…
A: 65% of the auto insurance claims submitted for property damage were submitted by males under 25…
Q: Events A1, A2 and Az form a partiton of the sample space S with probabilities P(A) = 0.2, P(A2) =…
A: The given probabilities are, The probability of event E is,
Q: Exercise 4. A certain species of plant always has either three or five leaves. The number is random,…
A: We know that, for two independent event A,BP(A∩B)=P(A)P(B) A plant can have either 3 leaves or 5…
Q: An experiment consists of two independent trials. The outcomes of the first trial are A, B, and C,…
A: Given problem Given that An experiment consists of two independent trials. The outcomes of the…
Q: Let E and F be events of a sample space such that P(E)=0.40, P(F)=0.25 and P(EnF)=0.25. Find the…
A:
Q: What happens to trees over a five-year period? A study lasting more than 30 years found these…
A:
Q: xercise 4. A certain species of plant always has either three or five leaves. The number is ndom,…
A: Given: open closed P (leaves) 3 leaves N3, open N3, closed 0.4 5 leaves N5, open N5,…
Q: Given that A and B are two events with the following probabilities: P(A) =, P(A'|B) = and P(An B) =…
A: PA=38 PA'|B=512 PA∩B=116
Q: (a)Find the probability distribution of x. (Hint: Let S denote a homeowner who has insurance and F…
A: (a) Let x be the number among the four who have earthquake insurance which follows binomial…
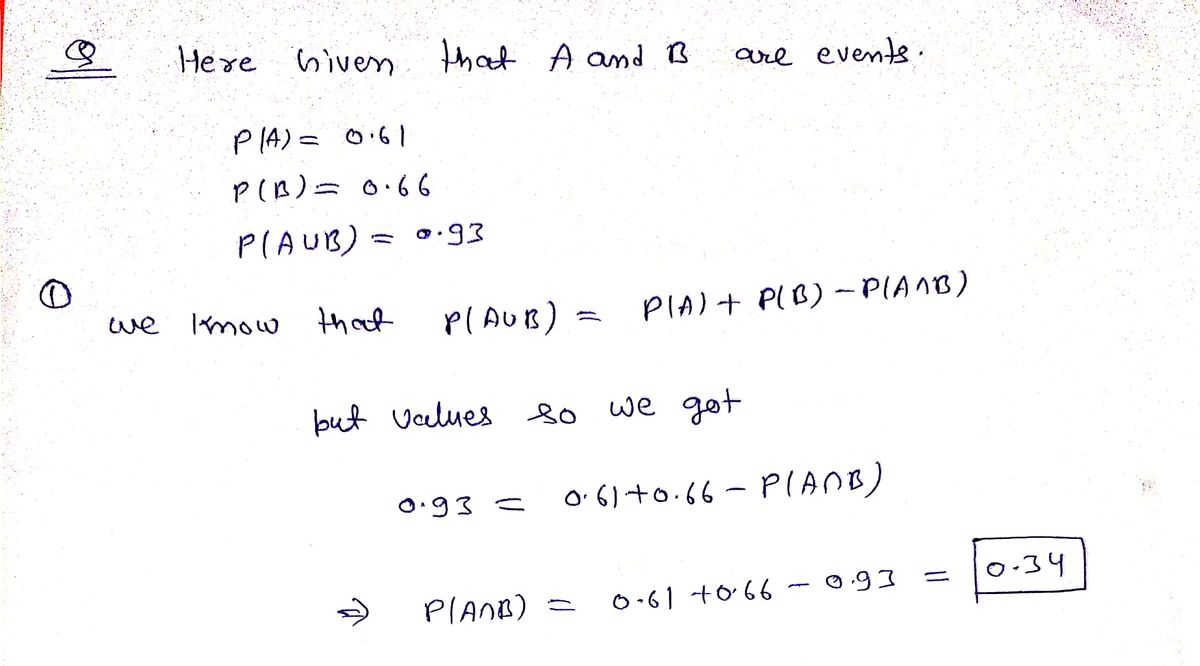
Step by step
Solved in 2 steps with 2 images
- When the health department tested private wells in a county for two impurities commonly found in drinking water, it found that 10% of the wells had neither impurity, 90% had impurity A, and 20% had impurity B. (Obviously, some had both impurities.) If a well is randomly chosen from those in the county, find the probability distribution for Y, the number of impurities found in the well. P(no impurities)= P(exactly one impurity)= P(both impurities)=O An oll company purchased an option on land in Alaska, Preliminary geologic studies assigned the following prior probabilities. P(high-quality oil) = 0.45 P(medium-quality oil) = 0.20 P(no oil) = 0.35 a. What is the probability of finding oll (to 2 decimals)? .65 b. After 200 feet of drilling on the first well, a soil test is taken, The probabilities of finding the particular type of soil identified by.the test are given below. P(soil|high-quality oil) = 0.25 %! P(soil medium-quality oil) = 0.85 P(soil no oil) = 0.25 Given the soil found in the test, use Bayes' theorem to compute the following revised probabilities (to 4 decimais). P(high-quality oiljsoil) P(medium-quality oil soil) P(no oilsoil) What is the new probability of finding oil (to 4 decimals)? According to the revised probabilities, what is the quality of oil that is most likely to be found? Select your answer O teon KeyA biologist estimates that the chance of germination for a type of bean seed is 0.7. A student was given 6 seeds. Let X be the number of seeds germinated from 6 seeds. Assuming that the germination of seeds are independent, explain why the distribution of X is binomial. What are the values of n and p? What are the probabilities that he gets (a) all seeds germinated, (b) just one seed not germinated, and (c) at most four seeds germinated?
- Yes, because (0.63)(0.63) = 0.497 No, because (0.63)(0.63) ≠ 0.497 Yes, because 63% + 63% = 49.7% No, because 63% + 63% ≠ 49.7%Q.No.3. (a) A bag contains 12 balls, 4 of which are red, 3 black and 5 green. Three balls are drawn from the bag. Find the probability that (i) all three are green (ii) The first is red, second is green and third is black. (b) A sale person has a 40% chance of making a sale to any customer who is called upon. If 18 calls are made, what is the probability that (i) at most 3 sales are made (ii) at least 17 sales are made.An experiment can result in one of five equally likely simple events, E₁, E₂, A: E₂, E4 2' P(A) = = 0.4 B: E₁, E3, E4, E5 P(B) = 0.8 C: E₂, E3 Refer to the following probabilities. P(A n B) = 0.2 P(AIB) = 0.25 P(BIA) P(BU C) = 1 P(BIC) 0.5 P(CIB) 0.25 Use the Addition and Multiplication Rules to find the following probabilities. (a) P(AUB) (b) P(An B) = 0.5 P(A U B) = ---Select--- + ---Select--- ✓ P(A n B) = ---Select--- (c) P(B n C) Yes P(B n C) = ---Select--- No P(C) = 0.4 . P(B) = = P(C) = = ---Select--- V = Do the results agree with those obtained by listing the simple events in each? P(A U B) = P({E₁, E₂, E3, E4, E5}) = 1 P(A n B) = P({E₁}) = 0.2 P(B n C) = P({E3}) = 0.2 .., E5. Events A, B, and C are defined as follows.
- Exercise 4. A certain species of plant always has either three or five leaves. The number is random, with P(3 leaves) 0.4 and P(5 leaves) = 0.6. Each plant has a flower which, randomly, is either open or closed, with probabilities P(open) = 0.8 and P(closed) = 0.2. A botanist collects 1000 randomly chosen plants from this species and nds the following distribution of traits: open closed N3,closed 3 leaves N3,open 5 leaves NE,open N5, closed a) Assuming the two traits are independent, determine the expectations of the counts №3,open, N3,closed, N5,0-en, and N5,close in the table. b) Determine an approximate value for the probability P(N3,open > 340). Exercise 5. Assume that we have observed the following values from a normal distribution with known variance o2 = and unknown mean . 1.23 -0.67 1.16 1.67 0.24 2.99 0.02 .17 0.27 21. Test the hypothesis Ho: = 0 against the alternative H₁: #0 at significance level a = 5%. Exercise 6. Let 0> 0 and XU[0,0], i.e. X is uniformly distributed on…Let A, B and C be events from a common sample space such that: P(A) = 0.72, P(B) = 0.56, P(C) =0.25, P(ANB) = 0.42. P(ANC) = 0.18, P(BOC) =0 %3D Compute P(AUBUC).A hospital reports that two patients have been admitted who have contracted Crohn's disease. Suppose our experiment consists of observing whether each patient survives or dies as a result of the disease. The simple events and probabilities of their occurrences are shown in the table (where S in the first position means that patient 1 survives, D in the first position means that patient 1 dies, etc.). Simple Events Probabilities SS 0.52 SD 0.20 DS 0.14 DD 0.14 Find the probability that both patients survive.
