Soive the resulting equations symbolically. . Check that your answer has the correct dimensions and satisfies special cases. • If numbers are given in the problem, plug them in and check that the answer makes sense. • Think about generalizations or simplifications of the problem. As an example, we will apply this procedure to find the acceleration of a block of mass m₂ that is pulled up a frictionless plane inclined at angle with respect to the horizontal by a massless string that passes over a massless, frictionless pulley to a block of mass m₁ that is hanging vertically. (Figure 1) igure N block 2 m₂a m₂g mig N block 2 a m₂a m₂g block 1 I migma C с N ma block block T 1 2 m₂g N block 2 T b m₂a m₂8 mig mig 17₁ d block 1 17₂ block 1 | m₁a 2 of 2 ▼ Part E What is F2, the sum of the x components of the forces acting on block 2? Take forces acting up the incline to be positive. Express your answer in terms of some or all of the variables tension T, m₂, g, and 0. View Available Hint(s) myaz = Σ F = Submit [5] ΑΣΦ Part F Complete previous part(s) Part G Complete previous part(s) Part H Complete previous part(s) Provide Feedback ?
Soive the resulting equations symbolically. . Check that your answer has the correct dimensions and satisfies special cases. • If numbers are given in the problem, plug them in and check that the answer makes sense. • Think about generalizations or simplifications of the problem. As an example, we will apply this procedure to find the acceleration of a block of mass m₂ that is pulled up a frictionless plane inclined at angle with respect to the horizontal by a massless string that passes over a massless, frictionless pulley to a block of mass m₁ that is hanging vertically. (Figure 1) igure N block 2 m₂a m₂g mig N block 2 a m₂a m₂g block 1 I migma C с N ma block block T 1 2 m₂g N block 2 T b m₂a m₂8 mig mig 17₁ d block 1 17₂ block 1 | m₁a 2 of 2 ▼ Part E What is F2, the sum of the x components of the forces acting on block 2? Take forces acting up the incline to be positive. Express your answer in terms of some or all of the variables tension T, m₂, g, and 0. View Available Hint(s) myaz = Σ F = Submit [5] ΑΣΦ Part F Complete previous part(s) Part G Complete previous part(s) Part H Complete previous part(s) Provide Feedback ?
College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
Related questions
Question

Transcribed Image Text:**Learning Goal:**
Once you have decided to solve a problem using Newton's 2nd law, there are steps that will lead you to a solution. One such prescription is the following:
- Visualize the problem and identify special cases.
- Isolate each body and draw the forces acting on it.
- Choose a coordinate system for each body.
- Apply Newton's 2nd law to each body.
- Write equations for the constraints and other given information.
- Solve the resulting equations symbolically.
- Check that your answer has the correct dimensions and satisfies special cases.
- If numbers are given in the problem, plug them in and check that the answer makes sense.
- Think about generalizations or simplifications of the problem.
As an example, we will apply this procedure to find the acceleration of a block of mass \( m_2 \) that is pulled up a frictionless plane inclined at angle \( \theta \) with respect to the horizontal by a massless string that passes over a massless, frictionless pulley to a block of mass \( m_1 \) that is hanging vertically. (Figure 1)
**Figure Description:**
The diagram shows a block, labeled as "block 2," resting on a frictionless inclined plane. The plane is inclined at an angle \( \theta \) with respect to the horizontal. Block 2 is connected by a string that runs over a pulley at the top of the inclined plane. This string connects to "block 1," which hangs vertically off the edge of the plane. The pulley is described as massless and frictionless. The configuration illustrates a classic physics problem related to Newton’s laws of motion.
![### Transcription for Educational Website
#### Problem-Solving Strategy
- **Solve equations symbolically:** Analyze equations for general expressions.
- **Dimensional consistency:** Ensure solutions have the correct dimensions and consider specific cases.
- **Verification with numbers:** Substitute numbers to check if the provided answer is logical.
- **Generalizations and simplifications:** Reflect on possible simplifications in the problem-solving process.
#### Application Example
We will use these strategies to find the acceleration of a block with mass \( m_2 \) on a frictionless inclined plane at angle \( \theta \). The block is connected via a massless string over a pulley to another block with mass \( m_1 \) that hangs vertically.
**Reference:** See Figure 1 for illustration.
---
#### Figure 1 Explanation
**Figure includes four subfigures (a, b, c, d):**
- **a:** Depicts a block (1) with mass \( m_1 \) on a vertical plane with forces \( m_1 g \) and \( N \) (normal force) acting on it.
- **b:** Displays block (2) with mass \( m_2 \) on an inclined plane, and forces \( T_2 \) (tension), \( N \), and \( m_2 g \) (gravitational force) acting on it.
- **c:** Shows force resolution of block (2) with components \( N \), \( T_2 \), and resolved gravitational forces \( m_2 g \sin \theta \) and \( m_2 g \cos \theta \).
- **d:** Illustrates block (1) with the forces \( T_1 \) (tension), \( m_1 g \), and acceleration \( m_1 a \).
---
#### Problem Part E
**Objective:** Determine \( \sum F_{x2} \), the sum of the \( x \)-components of the forces on block 2, taking positive as forces up the incline.
**Instructions:** Express the solution in terms of variables \( T \) (tension), \( m_2 \), \( g \) (gravity), and \( \theta \) (angle).
\[ m_2 a_{x2} = \sum F_{x2} = \]
**User Task:** Complete parts F, G, and H, building upon previous solutions.
For detailed guidance, refer to hints](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff0fdd9be-9990-44a9-8005-60989cbb2f12%2F1e02f5e7-52c9-48d8-850b-2544b58f47fe%2F2tq78l_processed.png&w=3840&q=75)
Transcribed Image Text:### Transcription for Educational Website
#### Problem-Solving Strategy
- **Solve equations symbolically:** Analyze equations for general expressions.
- **Dimensional consistency:** Ensure solutions have the correct dimensions and consider specific cases.
- **Verification with numbers:** Substitute numbers to check if the provided answer is logical.
- **Generalizations and simplifications:** Reflect on possible simplifications in the problem-solving process.
#### Application Example
We will use these strategies to find the acceleration of a block with mass \( m_2 \) on a frictionless inclined plane at angle \( \theta \). The block is connected via a massless string over a pulley to another block with mass \( m_1 \) that hangs vertically.
**Reference:** See Figure 1 for illustration.
---
#### Figure 1 Explanation
**Figure includes four subfigures (a, b, c, d):**
- **a:** Depicts a block (1) with mass \( m_1 \) on a vertical plane with forces \( m_1 g \) and \( N \) (normal force) acting on it.
- **b:** Displays block (2) with mass \( m_2 \) on an inclined plane, and forces \( T_2 \) (tension), \( N \), and \( m_2 g \) (gravitational force) acting on it.
- **c:** Shows force resolution of block (2) with components \( N \), \( T_2 \), and resolved gravitational forces \( m_2 g \sin \theta \) and \( m_2 g \cos \theta \).
- **d:** Illustrates block (1) with the forces \( T_1 \) (tension), \( m_1 g \), and acceleration \( m_1 a \).
---
#### Problem Part E
**Objective:** Determine \( \sum F_{x2} \), the sum of the \( x \)-components of the forces on block 2, taking positive as forces up the incline.
**Instructions:** Express the solution in terms of variables \( T \) (tension), \( m_2 \), \( g \) (gravity), and \( \theta \) (angle).
\[ m_2 a_{x2} = \sum F_{x2} = \]
**User Task:** Complete parts F, G, and H, building upon previous solutions.
For detailed guidance, refer to hints
Expert Solution
Step 1: Free body diagram of second mass
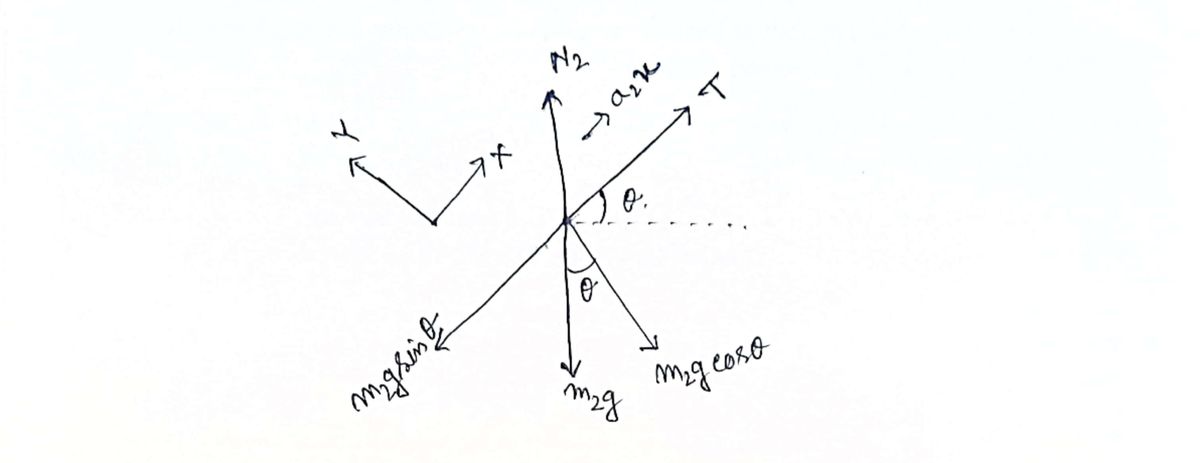
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
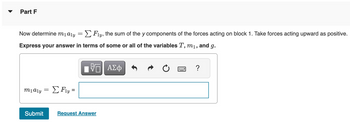
Transcribed Image Text:Part F
Now determine m₁a₁y = Σ Fly, the sum of the y components of the forces acting on block 1. Take forces acting upward as positive.
Express your answer in terms of some or all of the variables T, m₁, and g.
VE ΑΣΦ
m1aly
=
Σ Fy =
Submit Request Answer
?
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley

College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON