Answered: Show that for any function f(x) and the… | bartleby

Related questions

Question

**Quantum Mechanics: Show That**

In quantum mechanics, demonstrate that for any function \( f(x) \) and the momentum operator \( p_x \), the following operator relation holds:

\[
[f(x), p_x] = i \hbar \left( \frac{df}{dx} \right)
\]

**Hint:** Consider how the operators interact with a wavefunction positioned to their right.

Expert Solution

Step 1: To prove

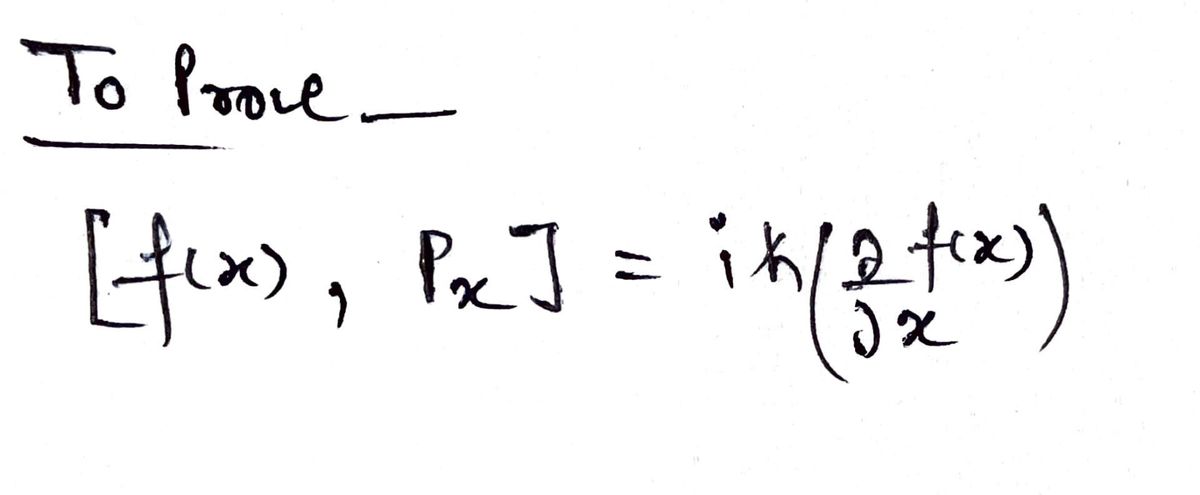
Step by step

Solved in 3 steps with 3 images

SEE SOLUTION Check out a sample Q&A here

Blurred answer

Similar questions

a) Show explicitly (by calculation) that the <p> = <p>* is fulfilled for the expectation value of themomentum. b) The three expressions xp, px and (xp+px)/2 are equivalent in classical mechanics.Show that for corresponding quantum mechanical operators in the orders shown, that <Q> = <Q>* isfulfilled by one of these operators, but not by the other two.
By employing the prescribed definitions of the raising and lowering operators pertaining to the one-dimensional harmonic oscillator: x = ħ 2mω -(â+ + â_) hmw ê = i Compute the expectation values of the following quantities for the nth stationary staten. Keep in mind that the stationary states form an orthogonal set. 2 · (â+ − â_) [ pm 4ndx YmVndx = 8mn a. The position of particle (x) b. The momentum of the particle (p). c. (x²) d. (p²) e. Confirm that the uncertainty principle is satisfied for all values of n
The wavefunction for the motion of a particle on a ring is of the form ψ=NeimΦ . Evaluate the normalization constant, N. Show full and complete procedure in a clear way. DO NOT SKIP ANY STEP
Plot the first three wavefunctions and the first three energies for the particle in a box of length L and infinite potential outside the box. Do these for n = 1, n = 2, and n = 3
Suppose that the wave function for a system can be written as 4(x) = √3 4 · Φι(x) + V3 2√₂ $2(x) + 2 + √3i 4 $3(x) and that 1(x), 2(x), and 3(x) are orthonormal eigenfunc- tions of the operator Ekinetic with eigenvalues E₁, 2E₁, and 4E₁, respectively. a. Verify that (x) is normalized. b. What are the possible values that you could obtain in measuring the kinetic energy on identically prepared systems? c. What is the probability of measuring each of these eigenvalues? d. What is the average value of Ekinetic that you would obtain from a large number of measurements?
what are the possible results that may be obtained upon measuring the property lz on a particle in a particular state, if its wavefunction is known to be Ψ, which is an eigenfunction of l2 such that l2Ψ=12ℏΨ? SHOW FULL AND COMPLETE PROCEDURE IN A CLEAR AND ORDERED WAY
Consider a particle moving in a 2D infinite rectangular well defined by V = 0 for 0 < x < L₁ and 0 ≤ y ≤ L2, and V = ∞ elsewhere. Outside the well, the wavefunction (x, y) is zero. Inside the well, the wavefunction (x, y) obeys the standing wave condition in the x and y direction, so it is given as: where A is a constant. (x, y) = Asin(k₁x) sin(k₂y), (a) The wavenumber k₁ in the x direction is quantized in terms of an integer n₁. Using the standing wave condition, find the possible values of k₁. (1) (b) The wavenumber k2 in the y direction is quantized in terms of a different integer n₂. Using the standing wave condition, find the possible values of k₂. (1) (c) Each state of the 2D infinite rectangular well is defined by the pair of quantum numbers (n₁, n₂). What is the energy of the state Eni,n₂? JXZ1