Proofs Task 4 (portfolio). Let an be a sequence decreasing to zero. Prove that En-1(-1)"an converges.
Proofs Task 4 (portfolio). Let an be a sequence decreasing to zero. Prove that En-1(-1)"an converges.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Need help with Task 4, this is a homework question not an exam

Transcribed Image Text:Due: September 20, 2023
Meta Tasks
Sorry this one is late, take until Monday if you want.
Task 1. Prove that the sequence an converges. The sequence is defined by ao = √2 and an = √2+an-1.
Task 2. Let an be a sequence such that every open interval containing 3 has infinitely many points from the sequence.
Similarly every open interval containing -2 has infinitely many points from the sequence. For every x -2,3 there
exists an open interval around a such that the interval only contains finitely many points from the sequence.
Say as much as you can about this sequence.
Task 3. Prove, including all relevant details, what interval the following series converges absolutely on. Check what
happens at the endpoints.
n=1
(x - 3)"
2n(n-1)
Proofs
Task 4 (portfolio). Let an be a sequence decreasing to zero. Prove that n=1(-1)"an converges.
Task 5. Let an be a positive sequence that decreases to zero. Set
Fall 2023
N
SN = Σa an.
n=1
Is lim sup Sy necessarily finite? Provide either a proof that it is or a counterexample that it isn't always.
Task 6. Prove Proposition 1.3.10.
•Every open interval has -2 and
3
Expert Solution
Step 1: Let sequence
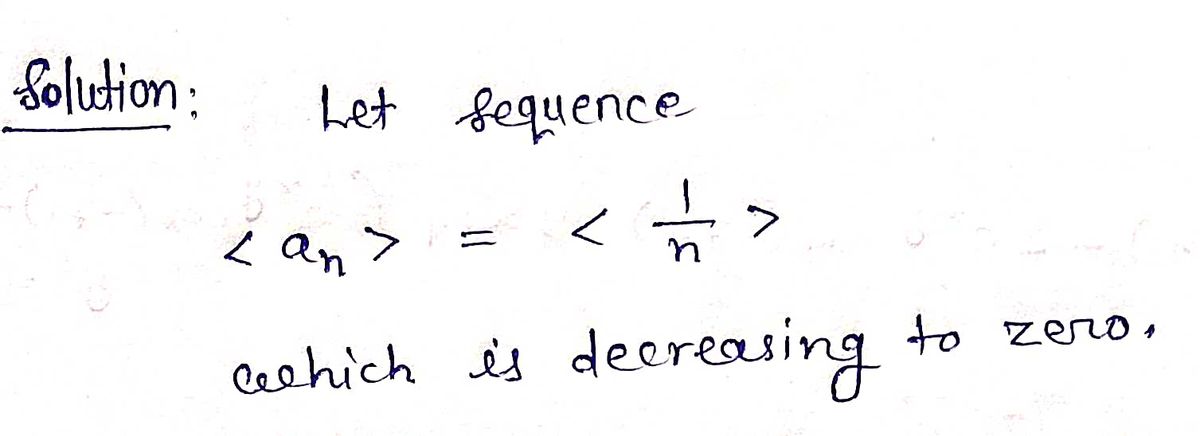
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

