Consider a block of mass m attached to a spring with force constant k, as shown in the figure(Figure 1). The spring can be either stretched or compressed. The block slides on a frictionless horizontal surface, as shown. When the spring is relaxed, the block is located at x=0. If the block is pulled to the right a distance A and then released, A will be the amplitude of the resulting
Consider a block of mass m attached to a spring with force constant k, as shown in the figure(Figure 1). The spring can be either stretched or compressed. The block slides on a frictionless horizontal surface, as shown. When the spring is relaxed, the block is located at x=0. If the block is pulled to the right a distance A and then released, A
will be the amplitude of the resulting oscillations.
Assume that the mechanical energy of the block-spring system remains unchanged in the subsequent motion of the block.
Part A
After the block is released from x=A, it will?
Part B
If the period is doubled, the frequency is?
Part C
An oscillating object takes 0.10 s to complete one cycle; that is, its period is 0.10 s. What is its frequency f?
Part D
If the frequency is 40 Hz, what is the period T ?
Part E
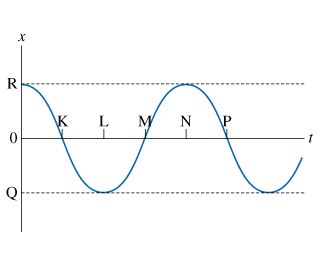
Which points on the x axis are located a distance A from the equilibrium position?
Part F
Suppose that the period is T. Which of the following points on the t axis are separated by the time interval T?
Part G
What is the period T ?
Part H
How much time t does the block take to travel from the point of maximum displacement to the opposite point of maximum displacement?
Part I
What distance d does the object cover during one period of oscillation?
Part J
What distance d does the object cover between the moments labeled K and N on the graph?


Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Could you help me with this question, please? If necessary, I can ask this in two questions.
Consider a block of mass m attached to a spring with force constant k, as shown in the figure(Figure 1). The spring can be either stretched or compressed. The block slides on a frictionless horizontal surface, as shown. When the spring is relaxed, the block is located at x=0. If the block is pulled to the right a distance A and then released, A will be the amplitude of the resulting oscillations.
Assume that the mechanical energy of the block-spring system remains unchanged in the subsequent motion of the block.
Part G
What is the period T ?
Part H
How much time t does the block take to travel from the point of maximum displacement to the opposite point of maximum displacement?
Part I
What distance d does the object cover during one period of oscillation?
Part J
What distance d does the object cover between the moments labeled K and N on the graph?