ou Answered orrect Answer An R=88MN resistor and a C=43μF capacitor are connected in series with a open switch and an V = 45.4V potential source. The capacitor is initially uncharged. The switch is closed at t = 0. Determine the current in the circuit when the charge on the capacitor is 1/9 of its maximum value (in μA). 47.6 0.4586 margin of error +/- 1%
ou Answered orrect Answer An R=88MN resistor and a C=43μF capacitor are connected in series with a open switch and an V = 45.4V potential source. The capacitor is initially uncharged. The switch is closed at t = 0. Determine the current in the circuit when the charge on the capacitor is 1/9 of its maximum value (in μA). 47.6 0.4586 margin of error +/- 1%
College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
Related questions
Concept explainers
Ohm's law
Ohm’s law is a prominent concept in physics and electronics. It gives the relation between the current and the voltage. It is used to analyze and construct electrical circuits. Ohm's law states that the voltage across a conductor is directly proportional to the current flowing through it.
Path of Least Resistance
In a series of alternate pathways, the direction of least resistance is the actual or metaphorical route that offers the least resistance to forwarding motion by a given individual or body.
Question
An R=88MS resistor and a C =43. capacitor are connected in
series with a open switch and an V = 45.4V potential source. The
capacitor is initially uncharged. The switch is closed at t = 0. Determine
the current in the circuit
when the charge on the capacitor is 1/9 of its maximum value (in p.A).
I need to look. At correct answer and show all work please
![### Problem Description
An \( R = 88 \, M\Omega \) resistor and a \( C = 43 \, \mu F \) capacitor are connected in series with an open switch and a \( V = 45.4 \, V \) potential source. The capacitor is initially uncharged. The switch is closed at \( t = 0 \). Determine the current in the circuit when the charge on the capacitor is \( \frac{1}{9} \) of its maximum value (in \( \mu A \)).
### Your Answer
47.6
### Correct Answer
0.4586 with a margin of error of +/- 1%
### Explanation
This problem deals with a basic RC (resistor-capacitor) charging circuit. When the switch is closed, the capacitor begins to charge through the resistor until it reaches its maximum charge, \( Q_{\text{max}} = C \cdot V \). The charge at any time \( t \) is given by \( Q(t) = Q_{\text{max}} \cdot (1 - e^{-t/RC}) \).
To find the current when the charge is \( \frac{1}{9} \) of \( Q_{\text{max}} \), you can use the relationship:
\[ Q(t) = \frac{1}{9} Q_{\text{max}} \]
The current \( I(t) \) in the circuit at time \( t \) is:
\[ I(t) = \frac{V}{R} \cdot e^{-t/RC} \]
Through solving, you find:
1. \( t = RC \cdot \ln(9) \)
2. \( I(t) = \frac{V}{R} \cdot \left(\frac{1}{9}\right) = \frac{45.4}{88 \times 10^6} \cdot \frac{1}{9} \)
This results in the correct answer approximately 0.4586 \( \mu A \).
The discrepancy between the given answer of 47.6 and the correct answer 0.4586 likely stems from a miscalculation involving either the natural logarithm, unit conversion, or arithmetic.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fee22cf2f-b974-4b00-a3cf-09b388e7d65d%2Fcbc98d4d-e1a7-4c0b-8bdf-19ec2ffc2ef0%2Fbxaipce_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Description
An \( R = 88 \, M\Omega \) resistor and a \( C = 43 \, \mu F \) capacitor are connected in series with an open switch and a \( V = 45.4 \, V \) potential source. The capacitor is initially uncharged. The switch is closed at \( t = 0 \). Determine the current in the circuit when the charge on the capacitor is \( \frac{1}{9} \) of its maximum value (in \( \mu A \)).
### Your Answer
47.6
### Correct Answer
0.4586 with a margin of error of +/- 1%
### Explanation
This problem deals with a basic RC (resistor-capacitor) charging circuit. When the switch is closed, the capacitor begins to charge through the resistor until it reaches its maximum charge, \( Q_{\text{max}} = C \cdot V \). The charge at any time \( t \) is given by \( Q(t) = Q_{\text{max}} \cdot (1 - e^{-t/RC}) \).
To find the current when the charge is \( \frac{1}{9} \) of \( Q_{\text{max}} \), you can use the relationship:
\[ Q(t) = \frac{1}{9} Q_{\text{max}} \]
The current \( I(t) \) in the circuit at time \( t \) is:
\[ I(t) = \frac{V}{R} \cdot e^{-t/RC} \]
Through solving, you find:
1. \( t = RC \cdot \ln(9) \)
2. \( I(t) = \frac{V}{R} \cdot \left(\frac{1}{9}\right) = \frac{45.4}{88 \times 10^6} \cdot \frac{1}{9} \)
This results in the correct answer approximately 0.4586 \( \mu A \).
The discrepancy between the given answer of 47.6 and the correct answer 0.4586 likely stems from a miscalculation involving either the natural logarithm, unit conversion, or arithmetic.
Expert Solution
Step 1: Analysis of given information
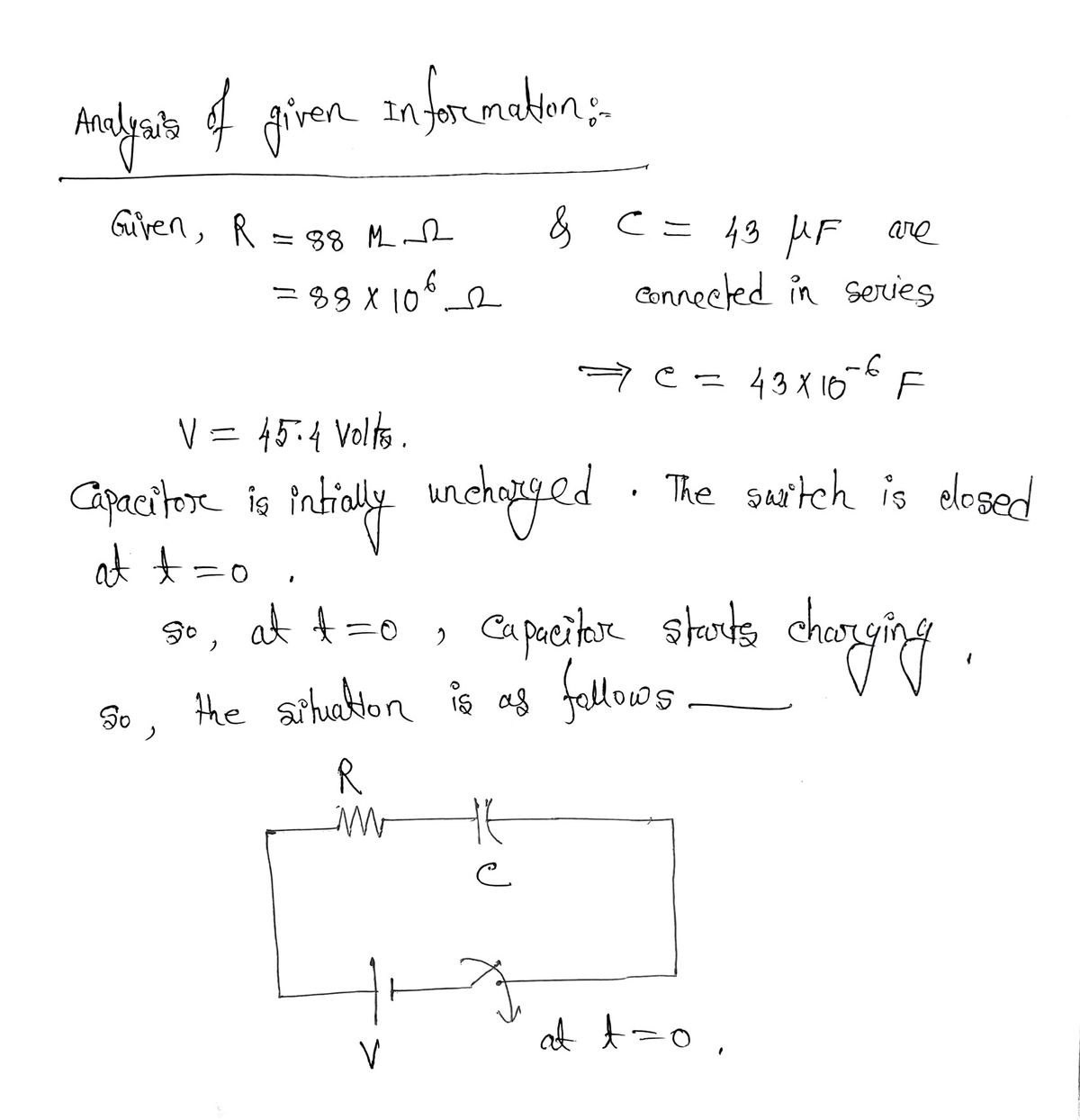
Step by step
Solved in 5 steps with 5 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley

College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON