Let r denote the radial distance from the center of the insulating cylinder. To solve Gauss' law in all space, there are four (4) regions to consider. The result for the electric field E(r) in regions I- III are given below E₁(r) = E(r)=E()= -Tf 2€0 pR² 1 I claim Ey (r) is 260 T Em (r) = 0 I claim AVab is f Using Gauss' law, derive the expression for E(r) in region IV, where r > Rc. r< Ra Ra
Let r denote the radial distance from the center of the insulating cylinder. To solve Gauss' law in all space, there are four (4) regions to consider. The result for the electric field E(r) in regions I- III are given below E₁(r) = E(r)=E()= -Tf 2€0 pR² 1 I claim Ey (r) is 260 T Em (r) = 0 I claim AVab is f Using Gauss' law, derive the expression for E(r) in region IV, where r > Rc. r< Ra Ra
Related questions
Question

Transcribed Image Text:An infinitely long, solid insulating cylinder with radius Ra is placed concentric within a
conducting cylindrical shell of inner radius R, and outer radius Re. The inner cylinder has a uniform
volume charge density +lpl, and the outer cylinder has a net linear charge density of -3121.
Assume Ip Rå| > |32| for all parts.

Transcribed Image Text:Letr denote the radial distance from the center of the insulating cylinder. To solve Gauss' law in
all space, there are four (4) regions to consider. The result for the electric field E(r) in regions l-
III are given below
E(r)=
=
Ē₁ (r) = rf
2€0
pR² 1
E₁ (r)
I claim Avab is
260 T
Em (r) = 0
I claim Ey (r) is
f
Using Gauss' law, derive the expression for E(r) in region IV, where r > Rc.
Make a statement on the term in parenthesis in E (1).
r< Ra
Ra<r < Rp
Rp <r < Re
Ev (r) =
PR (1
2€0
3λ
(1 - 03/12 - ) / / *
What is the electric potential difference between the inner surface of the conducting cylinder
and the outer surface of the insulating cylinder (in region II)? Hint: See the result from part b for
Ē₁ (r).
AVab= V(R₂) - V(Ra)
PRå
260
(RD)
log
Explicitly point out in each step which terms in the derivation contribute negative signs.
Expert Solution
Step 1
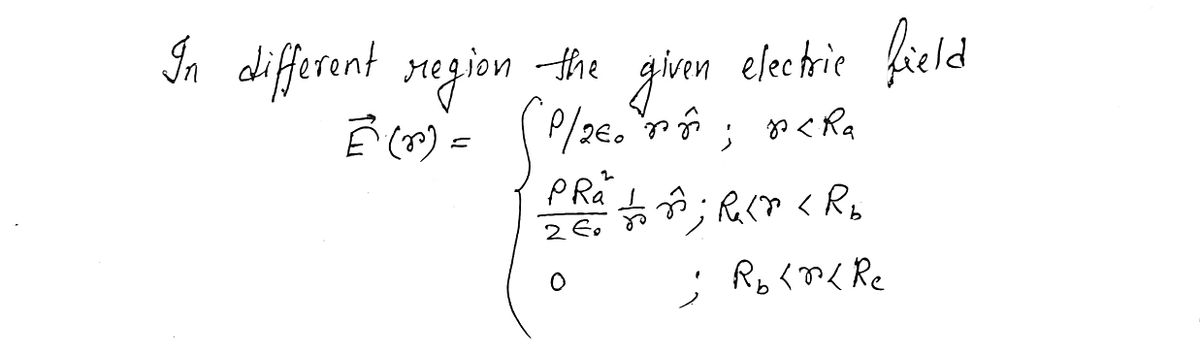
Step by step
Solved in 2 steps with 2 images
