It takes an average of 13.5 minutes for blood to begin clotting after an injury. An EMT wants to see if the average will increase if the patient is immediately told the truth about the injury. The EMT randomly selected 63 injured patients to immediately tell the truth about the injury and noticed that they averaged 13.6 minutes for their blood to begin clotting after their injury. Their standard deviation was 1.35 minutes. What can be concluded at the the αα = 0.10 level of significance? For this study, we should use Select an answer t-test for a population mean z-test for a population proportion The null and alternative hypotheses would be: H0:H0: ? p μ Select an answer ≠ = > < H1:H1: ? μ p Select an answer > ≠ = < The test statistic ? t z = (please show your answer to 3 decimal places.) The p-value = (Please show your answer to 4 decimal places.) The p-value is ? ≤ > αα Based on this, we should Select an answer fail to reject accept reject the null hypothesis. Thus, the final conclusion is that ... The data suggest the population mean is not significantly greater than 13.5 at αα = 0.10, so there is statistically significant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is equal to 13.5. The data suggest that the population mean is not significantly greater than 13.5 at αα = 0.10, so there is statistically insignificant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is greater than 13.5. The data suggest the populaton mean is significantly greater than 13.5 at αα = 0.10, so there is statistically significant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is greater than 13.5.
It takes an average of 13.5 minutes for blood to begin clotting after an injury. An EMT wants to see if the average will increase if the patient is immediately told the truth about the injury. The EMT randomly selected 63 injured patients to immediately tell the truth about the injury and noticed that they averaged 13.6 minutes for their blood to begin clotting after their injury. Their standard deviation was 1.35 minutes. What can be concluded at the the αα = 0.10 level of significance?
- For this study, we should use Select an answer t-test for a population
mean z-test for a population proportion - The null and alternative hypotheses would be:
H0:H0: ? p μ Select an answer ≠ = > <
H1:H1: ? μ p Select an answer > ≠ = <
- The test statistic ? t z = (please show your answer to 3 decimal places.)
- The p-value = (Please show your answer to 4 decimal places.)
- The p-value is ? ≤ > αα
- Based on this, we should Select an answer fail to reject accept reject the null hypothesis.
- Thus, the final conclusion is that ...
- The data suggest the population mean is not significantly greater than 13.5 at αα = 0.10, so there is statistically significant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is equal to 13.5.
- The data suggest that the population mean is not significantly greater than 13.5 at αα = 0.10, so there is statistically insignificant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is greater than 13.5.
- The data suggest the populaton mean is significantly greater than 13.5 at αα = 0.10, so there is statistically significant evidence to conclude that the population mean time for blood to begin clotting after an injury if the patient is told the truth immediately is greater than 13.5.
(1)
Determine what type of test is used for testing for problem.
The type of test is used for testing for problem is obtained below :
The type of test used here is single mean because the claim is to test an average will increase if the patient is immediately told the truth about the injury or not. Moreover the population standard deviation is not known therefore, the type of test used here is t-test for a population mean.
Correct option: t-test for a population mean.
(2)
State the hypotheses.
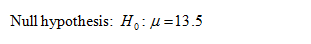
That is, there is no evidence to conclude that an average will increase if the patient is immediately told the truth about the injury.
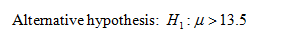
That is, there is evidence to conclude that an average will increase if the patient is immediately told the truth about the injury.
(1)
Obtain the value of the test statistic.
The value of the test statistic is obtained below:
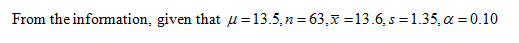
The required value is,
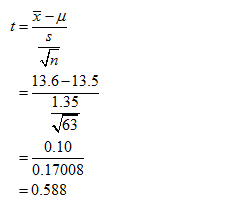
Thus, the value of the test statistic is 0.588.
(2 )
Obtain the degrees of degrees of freedom.
The degrees of freedom are obtained below:
From the information, given that there is a sample of 63.
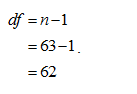
Thus, the degrees of freedom used are 62.
Use Excel to obtain the probability value.
Follow the instruction to obtain the P-value:
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=TDIST”
- Enter the test statistic as 0.588
- Enter the degrees of freedom as 62.
- Enter the tails as 1.
- Click enter
EXCEL output:
From the Excel output, the P-value is 0.2793
Thus, the P-value is 0.2793.
Step by step
Solved in 3 steps with 6 images









