Is there sufficient evidence at the a = 0.10 level to conclude that the proportion of this business's customers who are less than 25 years old is greater than 30%?
Is there sufficient evidence at the a = 0.10 level to conclude that the proportion of this business's customers who are less than 25 years old is greater than 30%?
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question

Transcribed Image Text:1:50
Making conclusions in a z test for a pr...
A business knew that 30% of its customers
were less than 25 years old. The business
wanted to increase this percentage, so they
created a marketing campaign that targeted
this age group. After the campaign, the
business obtained a random sample of 50
customers to test Ho: p = 0.3 versus
Ha : p > 0.3, where p is the proportion of
this business's customers who are less than
25 years old after the marketing campaign.
The business found that 36% of those
sampled were less than 25 years old. They
calculated a test statistic of z≈ 0.93 a P-
value of approximately 0.177 for these
results. Assume that the conditions for
inference were met.
α
Is there sufficient evidence at the
0.10 level to conclude that the
proportion of this business's customers
who are less than 25 years old is greater
than 30%?
-
5G 20
Stuck? Use a hint.
SC Do 4 problems
Check
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
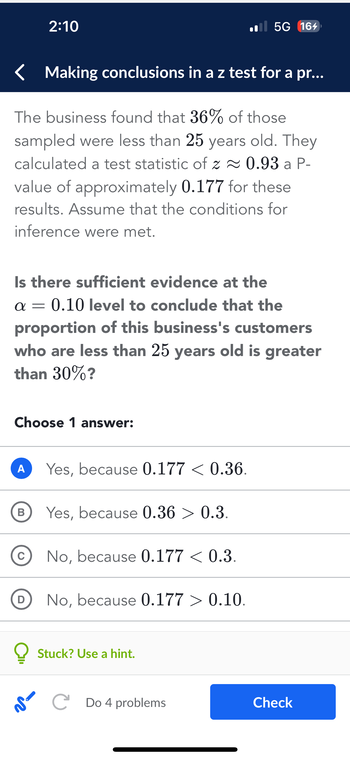
Transcribed Image Text:Making conclusions in a z test for a pr...
The business found that 36% of those
sampled were less than 25 years old. They
calculated a test statistic of z≈ 0.93 a P-
value of approximately 0.177 for these
results. Assume that the conditions for
inference were met.
Is there sufficient evidence at the
α=
0.10 level to conclude that the
proportion of this business's customers
who are less than 25 years old is greater
than 30%?
Choose 1 answer:
A
2:10
B
C
D
Yes, because 0.177 < 0.36.
Yes, because 0.36 > 0.3.
No, because 0.177 < 0.3.
No, because 0.177 > 0.10.
5G 164
Stuck? Use a hint.
SC Do 4 problems
Check
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman