Is the below matrix a Rotation or Reflection? Describe the resulting transformation. M = = √3 1 LIN 2 2 —— 1 2 N|T √3 2
Is the below matrix a Rotation or Reflection? Describe the resulting transformation. M = = √3 1 LIN 2 2 —— 1 2 N|T √3 2
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Matrix Transformation: Rotation or Reflection?**
The matrix \( M \) is given as:
\[
M = \begin{pmatrix}
-\frac{\sqrt{3}}{2} & \frac{1}{2} \\
\frac{1}{2} & -\frac{\sqrt{3}}{2}
\end{pmatrix}
\]
**Analysis:**
To determine if the matrix represents a rotation or reflection, we need to analyze its properties:
1. **Determinant**:
- The determinant of a 2x2 matrix \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\) is calculated as \(ad - bc\).
- For matrix \( M \):
\[
\text{det}(M) = \left(-\frac{\sqrt{3}}{2}\right)\left(-\frac{\sqrt{3}}{2}\right) - \left(\frac{1}{2}\right)\left(\frac{1}{2}\right) = \frac{3}{4} - \frac{1}{4} = \frac{2}{4} = \frac{1}{2}
\]
- The determinant is \(\frac{1}{2}\), which is less common for rotation matrices as they usually have a determinant of 1, but indicates that this is not a standard rotation matrix with determinant -1, likely a reflection combined with a scaling factor.
2. **Orthogonality Check**:
- If a matrix’s transpose is equal to its inverse, the matrix is orthogonal.
- Here, it appears that this matrix involves a reflection, as typical orthogonal matrices used for rotation have a determinant of \(\pm 1\).
3. **Transformation Description**:
- The provided matrix looks like a combination of reflection along a certain axis and scaling, rather than a pure rotation matrix, due to its determinant being \(\frac{1}{2}\le 1 \).
**Conclusion:**
The matrix likely represents a reflection (due to the negative sign and non-standard determinant for simple rotations), but it's important to consider this within specific geometric contexts for full interpretation, and further check eigenvalues or confirm with additional geometric transformations for more precise classification.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fdaad9e7e-1f14-44d5-98ac-51623b651f9b%2F25fe5b47-5cb6-432f-86e9-355e740223c4%2F0vyl1ru_processed.png&w=3840&q=75)
Transcribed Image Text:**Matrix Transformation: Rotation or Reflection?**
The matrix \( M \) is given as:
\[
M = \begin{pmatrix}
-\frac{\sqrt{3}}{2} & \frac{1}{2} \\
\frac{1}{2} & -\frac{\sqrt{3}}{2}
\end{pmatrix}
\]
**Analysis:**
To determine if the matrix represents a rotation or reflection, we need to analyze its properties:
1. **Determinant**:
- The determinant of a 2x2 matrix \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\) is calculated as \(ad - bc\).
- For matrix \( M \):
\[
\text{det}(M) = \left(-\frac{\sqrt{3}}{2}\right)\left(-\frac{\sqrt{3}}{2}\right) - \left(\frac{1}{2}\right)\left(\frac{1}{2}\right) = \frac{3}{4} - \frac{1}{4} = \frac{2}{4} = \frac{1}{2}
\]
- The determinant is \(\frac{1}{2}\), which is less common for rotation matrices as they usually have a determinant of 1, but indicates that this is not a standard rotation matrix with determinant -1, likely a reflection combined with a scaling factor.
2. **Orthogonality Check**:
- If a matrix’s transpose is equal to its inverse, the matrix is orthogonal.
- Here, it appears that this matrix involves a reflection, as typical orthogonal matrices used for rotation have a determinant of \(\pm 1\).
3. **Transformation Description**:
- The provided matrix looks like a combination of reflection along a certain axis and scaling, rather than a pure rotation matrix, due to its determinant being \(\frac{1}{2}\le 1 \).
**Conclusion:**
The matrix likely represents a reflection (due to the negative sign and non-standard determinant for simple rotations), but it's important to consider this within specific geometric contexts for full interpretation, and further check eigenvalues or confirm with additional geometric transformations for more precise classification.
Expert Solution
Step 1: Given part
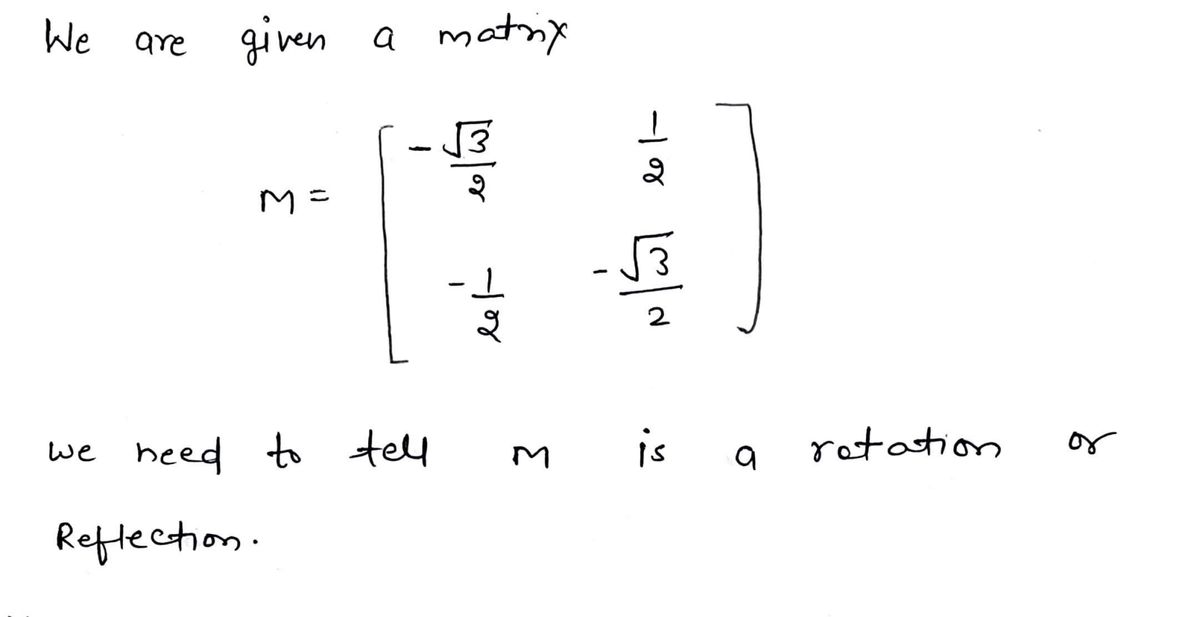
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

